促進初中生數學建模素養發展的教學策略研究
李愛民
摘要:促進初中生數學建模素養發展是現代教育背景下初中數學教學的基本目標之一.數學建模素養的發展有利于初中生空間想象與數學運算、邏輯思維與創新思維等多方面能力的提升.本文中通過大量的教學實踐活動,總結出促進初中生數學建模素養發展的教學策略.
關鍵詞:數學建模;核心素養;教學策略
數學的思想包括數、形以及數與形結合的推理過程.建模過程是學生綜合運用基本數學知識與數學思維去解讀生活中問題的成長歷程.因此,數學建模與素養發展息息相關,數學建模包括學生數學思維、自主實踐能力的培養、數學素養的構建等方面.促進初中生數學建模素養發展的教學策略研究是當下教育教學的需要.
1 搭建數與式的橋梁,激發學生的建模意識
意識是形成思維的前提,思維是形成素養的條件,它們是層層遞進、互相依賴的關系.在幫助學生發展數學建模素養時,首先創設學生關注的情境,通過興趣引導,激發建模意識,并將這種意識貫穿于數學訓練中,促使他們逐漸形成數學思維.
數學的思維是抽象的,教學過程中通常采用直觀的形式將實際問題轉化為抽象的數學問題,這種轉化就是幫助學生形成數學思維的過程,是對數學問題的建模.“直觀的形式”來源于生活現象,需要學生細致入微、靈活敏銳地觀察生活,然后試著以數學的思維去解讀生活實際.
例如,講授蘇科版八年級下冊“10.5分式方程”的應用時,在課堂解決問題環節創設以下情境.
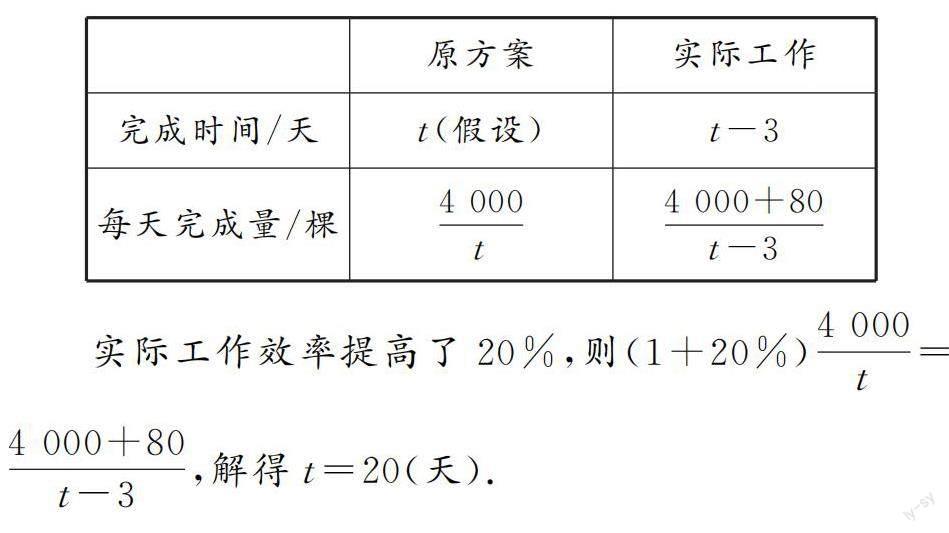
案例1 (2022年江蘇省泰州市中考試題)為了改善生態環境,某鄉村計劃植樹4 000棵.由于志愿者的支援,實際工作效率提高了20%,結果比原方案提前3天完成,并且多植樹80棵,原計劃植樹多少天?
分析:方法1——對比觀察法.
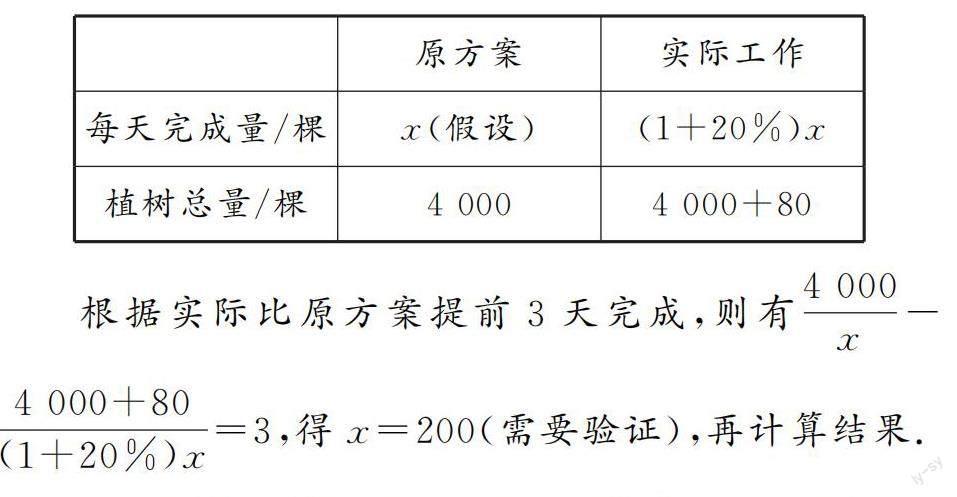
方法2:
通過案例1的分析可以發現,培養學生觀察生活現象的興趣和能力,有利于他們在課堂學習過程中自然而然地采用觀察法解決問題.案例1中的兩種分析,都是以比較觀察、量化觀察為線索,根據得到的現象進行思考,從而找出隱藏在現象背后的數學實質.
2 細挖教材知識內容,引導數學建模方法
初中生處于直觀思維活躍,而抽象思維逐漸形成的階段.數學是一種抽象化的解決實際問題的工具,掌握數學建模知識,需要將數學建模融入到學生數學學習中,需要教師對現有教材進行深入淺出的挖掘.學科素養的發展,更需要在授課過程中潛移默化地向學生傳遞建模方法,幫助他們提升數學學習能力,讓建模的難度循序漸進、逐步攀升.
如在學習蘇科版八年級上冊“6.4用一次函數解決問題”時,通過課題組的研究認為,在習題課環節,可以采用例題引導知識建模的方法.
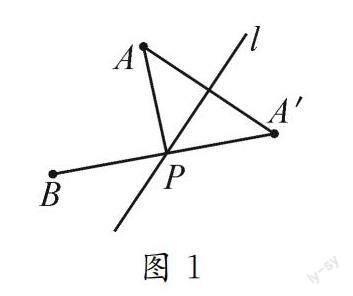
案例2 (2022年江蘇省南通市中考題改編)定義:如圖1,A,B為直線l同側的兩點,過點A作直線l的對稱點A′,連接A′B交直線l于點P,連接AP,那么稱點P為點A,B關于直線l的“等角點”.
運用:如圖2,在平面直角坐標系xOy中,A(2,√—3),B(-2,- √—3)兩點.關于直線x=4的等角點坐標是 .
分析:(遞進引導法)首先,用已有的知識點導入,要求學生回憶確定直線的方式.思考在圖2中如何作直線x=4?從y=kx+b模型出發,搭建與直線x=4的對應關系.
其次,引導學生思考“點B(-2,-3)關于直線x=4的對稱點B′坐標是什么?”本題是否僅此一種作法?
再次,引導學生思考——根據什么原則、怎么寫出直線AB′的方程?直線AB′與直線x=4的交點坐標如何求解?
課堂上在深入解讀基本數學知識的同時,引導學生從基于數學建模的問題解決方式入手,選取類似知識點以建模方式進行講解,有利于學生對數學思想的內化.通過課堂典例的引導,加深學生印象,并于適當時機對建模方法加以歸納總結、強化信息的提取、釋疑的策劃、模型的構建等,讓學生在思想的同化過程中發展數學建模素養.
3 思考生活實際問題,促進建模素養發展
將建模思維、方法運用到生活情境中去解決問題,是初中生對數學建模素養發展的深層次目標.在這一過程中,需要從初中生的學情出發,了解他們的學習特點及興趣,注意選材,將更多有趣的生活案例引入教學之中,并以數學建模的方式進行分析,使學生逐漸感受到用數學建模解疑生活實際的樂趣,進而激發學生自發進行建模活動.
在“不等式”復習課環節,課題組成員提出了引用如下一個案例.
案例3 (2022年江蘇省南通市中考題)小明購置A,B兩種商品,每次購置同一種商品的單價相同,具體信息如下表:
根據以上信息解答以下問題:
(1)求A,B兩種商品的單價;
(2)假設第三次購置這兩種商品共12件,且A種商品的數量不少于B種商品數量的2倍,請設計出最省錢的購置方案,并說明理由.
分析:(1)設A,B兩種商品的單價分別為x元和y元,根據題意不難得到二元一次方程
2x+y=55和x+3y=65,解得x=20,y=15.
(2)第三次購置這兩種商品共12件,若購置A,B種商品分別為a,b件,則a+b=12;A種商品的數量不少于B種商品數量的2倍,即a≥2b.由此可得0≤b≤4.故購置總費用為20a+15b.由20a+15b=20(12-b)+15b=240-5b,得當b=4,a=8時,最省錢.
案例3的問題情境與初中生的實際生活緊密相關,問題(1)屬于二元一次方程組的知識應用,也為問題(2)作鋪墊;問題(2)是不等式的應用,要解決的問題是設計出最省錢的購置方案,其實是利用不等式求最值.由此可見,中考試題問題設置的難度是逐步上升的,因此,課堂教學中的建模過程也應由淺入深,逐步夯實加固數學學科素養.
在教學中,從學生的實際學情出發,結合學生的數學建模能力合理安排問題梯度,以基礎知識帶動知識應用.多創設與生活情境相關的問題,多留給學生思考和探究空間,鼓勵學生創新出更多的建模思路.
總而言之,促進初中生數學建模素養發展的教學在于搭建數與式的橋梁,即對數與式的關聯進行建模,形成數學的基本思想方法;夯實教與學的環節,讓數學思維方法在基本的訓練過程中得到升華,從而使數學素養得以發展.
參考文獻:
[1]馬曉琴.科技創新活動中初中生數學建模素養塑造的策略[J].新課程,2021(45):163.
[2]余啟宏.初中生數學建模素養發展的教學策略[J].中學數學,2020(8):90-91.
[3]雷業紅,盧華嵐.初中數學教學中學生數學建模素養的培養策略分析[J].數學學習與研究,2022(6):113-115.

