創(chuàng)設(shè)質(zhì)疑情境的廣度，挖掘釋疑過(guò)程的深度

許昌軍

摘要：教育教學(xué)實(shí)踐表明，課改的目的是為了更好地“傳道授業(yè)解惑”.“情境+問(wèn)題串”的教學(xué)模式讓教與學(xué)事半功倍.在教師創(chuàng)設(shè)的數(shù)學(xué)問(wèn)題情境的引領(lǐng)下，學(xué)生興趣盎然，通過(guò)剖析情境、準(zhǔn)確領(lǐng)悟、自主探究、合作交流以及釋疑解疑，輕松實(shí)現(xiàn)數(shù)學(xué)課程每一單元中重要的教學(xué)內(nèi)容目標(biāo).

關(guān)鍵詞：質(zhì)疑情境；釋疑過(guò)程；初中數(shù)學(xué)

通過(guò)近幾年的教學(xué)實(shí)踐，課題組各位同仁駕馭“情境+問(wèn)題串”教學(xué)模式的技能不言而喻.在學(xué)科組集體備課時(shí)，每位教師對(duì)數(shù)學(xué)教材中的每一單元、每一個(gè)重要的教學(xué)內(nèi)容都創(chuàng)設(shè)出特定的質(zhì)疑情境，預(yù)設(shè)一連串的數(shù)學(xué)問(wèn)題，可謂是精彩紛呈，通過(guò)互相打磨和借鑒，形成適宜不同班級(jí)學(xué)情的預(yù)案.基于此，筆者談?wù)務(wù)n題組研究得出的最新成果——“情境+問(wèn)題串”助力學(xué)科素養(yǎng)的構(gòu)建.

1 創(chuàng)設(shè)質(zhì)疑的情境，激發(fā)探疑的興趣

數(shù)學(xué)思想來(lái)源于生活實(shí)際，是從生活現(xiàn)象中抽象出來(lái)的原理或法則.因此，數(shù)學(xué)課堂教學(xué)要從學(xué)生的生活經(jīng)驗(yàn)和已有的知識(shí)等學(xué)情出發(fā)，創(chuàng)設(shè)能夠激發(fā)學(xué)生興趣的質(zhì)疑情境，在學(xué)生的“圍觀”中開展觀察記錄、假設(shè)推理、操作演繹和交流探究等活動(dòng)，使學(xué)生通過(guò)活動(dòng)掌握基本數(shù)學(xué)思想，學(xué)會(huì)從數(shù)學(xué)的角度去觀察事物、思考問(wèn)題.

對(duì)于九年級(jí)數(shù)學(xué)學(xué)科組來(lái)說(shuō)，目前的教學(xué)重點(diǎn)是備考.下面是某次集體備課實(shí)錄.

案例1 九年級(jí)數(shù)學(xué)備課組集體備課實(shí)錄如下：

王：在學(xué)習(xí)本部分內(nèi)容之前，已講授了二次函數(shù)的概念和二次函數(shù)y=ax²，y=ax²+k，y=a（x-h）²的圖象和性質(zhì).學(xué)生有一定的關(guān)于二次函數(shù)知識(shí)的基礎(chǔ).

張：需要從如何畫二次函數(shù)的圖象入手，創(chuàng)設(shè)二次函數(shù)圖象與性質(zhì)研究方向的質(zhì)疑情境，直接指向中考，激發(fā)學(xué)生的興趣.

肖：可以采用近年來(lái)的中考試題創(chuàng)設(shè)質(zhì)疑情境.

選題1 （2022年江蘇省常州市中考第8題）已知二次函數(shù)y=x²+x-1/5，當(dāng)自變量x取m時(shí)對(duì)應(yīng)的值大于0，當(dāng)自變量x分別取m-1，m+1時(shí)對(duì)應(yīng)的函數(shù)值分別為y₁，y₂，判斷y₁，y₂的正負(fù).

預(yù)設(shè)目的是讓學(xué)生明確二次函數(shù)圖象為拋物線，產(chǎn)生的質(zhì)疑為：二次函數(shù)圖象上點(diǎn)的坐標(biāo)特點(diǎn)是什么？二次函數(shù)圖象與x軸有幾個(gè)交點(diǎn)？交點(diǎn)在什么位置？

選題2 （2022年江蘇省無(wú)錫市中考第27題）一次函數(shù)y=?x的圖象（略），它與二次函數(shù)y=ax²-4ax+c的圖象交于A，B兩點(diǎn)……

（1）求點(diǎn)C的坐標(biāo)；

（2）設(shè)二次函數(shù)圖象的頂點(diǎn)為D.①②……求此二次函數(shù)的關(guān)系式.

預(yù)設(shè)目的是讓學(xué)生能粗略繪出二次函數(shù)的圖象，并思考：怎樣繪出滿足條件的二次函數(shù)的圖象？怎樣應(yīng)用數(shù)形轉(zhuǎn)化思想？

王：選題2的難度過(guò)大，問(wèn)題（2）節(jié)選①即可.

張：我建議換個(gè)題目……

由案例1可以看出，預(yù)案都注重將課堂教學(xué)設(shè)定為從問(wèn)題情境入手，盡量拓展質(zhì)疑情境的廣度，從提供的背景材料（九年級(jí)可選取中考試題）、典例中獲取信息，通過(guò)存疑、探疑、交流釋疑等多方面來(lái)組織和實(shí)施教學(xué).這樣的課堂設(shè)計(jì)使得學(xué)生在課堂活動(dòng)中興趣被激發(fā)，自主探究被激活，在探疑和釋疑過(guò)程中形成知識(shí)與能力，自然而然提升學(xué)科素養(yǎng).

2 引導(dǎo)存疑的生成，推敲提取的信息

“問(wèn)題串”是實(shí)現(xiàn)學(xué)習(xí)目標(biāo)的有效手段之一，是給學(xué)生對(duì)新知進(jìn)行存疑與探疑的平臺(tái).換句話說(shuō)，課堂教學(xué)離不開“疑”，存疑是前提，探疑是過(guò)程，釋疑是目的，“疑”是展開課堂活動(dòng)的動(dòng)力源泉.因此，創(chuàng)設(shè)“問(wèn)題串”時(shí)，問(wèn)題要有指向性，通過(guò)質(zhì)疑情境，明確在該情境下想要探的“疑”是什么；同時(shí)，問(wèn)題要具有價(jià)值，因?yàn)榻虒W(xué)的三維目標(biāo)是“情感、態(tài)度與價(jià)值觀”，所以，需要幫助學(xué)生緊扣核心問(wèn)題進(jìn)行探疑，發(fā)展思維，培養(yǎng)學(xué)生多方面、多角度解疑的能力；另外，問(wèn)題還需具有寬泛性，把存疑與解疑聯(lián)系在一起，形成一定的探疑空間，從而在活動(dòng)中實(shí)現(xiàn)對(duì)數(shù)學(xué)思維的建模.

案例2 王老師在講授“全等三角形”的復(fù)習(xí)課時(shí)，課堂實(shí)錄片段如下：

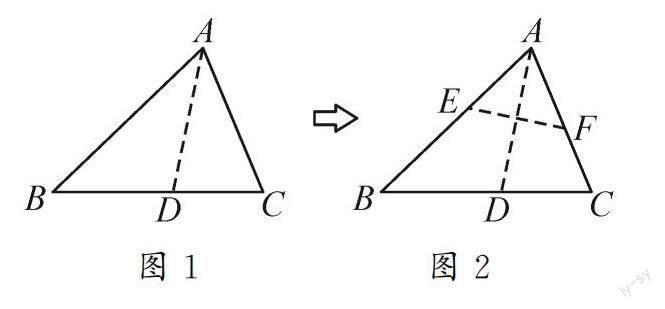
演示：取三角形紙片ABC（AB＞AC），沿過(guò)點(diǎn)A的直線折疊，使得AC落在AB邊上，折痕為AD，展開紙片（如圖1）；再次將該紙片折疊，重合點(diǎn)A和點(diǎn)D，折痕為EF，展平紙片（如圖2）.

活動(dòng)：

（1）觀察與發(fā)現(xiàn).△AEF是什么形狀的三角形？請(qǐng)說(shuō)明理由.

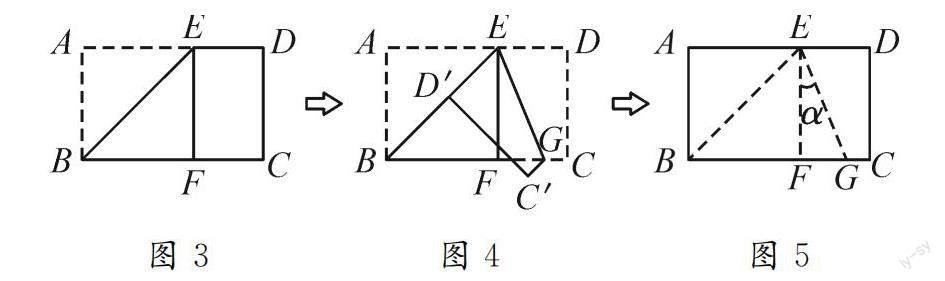
（2）實(shí)踐與應(yīng)用.讓學(xué)生拿出矩形紙片ABCD（BC＞AB），沿過(guò)點(diǎn)B的直線折疊，使點(diǎn)A落在BC邊上的點(diǎn)F處，折痕為BE（如圖3）；再沿過(guò)點(diǎn)E的直線折疊，使點(diǎn)D落在BE上的點(diǎn)D′處，折痕為EG（如圖4）；再展平紙片（如圖5）.

先測(cè)量圖5中∠α的大小，然后進(jìn)行計(jì)算推理.

（教師深入學(xué)生之中并引導(dǎo)開展活動(dòng).）

評(píng)析：王老師采用演示法創(chuàng)設(shè)的質(zhì)疑情境，大大激發(fā)了學(xué)生的興趣.提出的觀察與發(fā)現(xiàn)問(wèn)題有明確的指向性.同時(shí)，幫助學(xué)生進(jìn)一步進(jìn)行實(shí)踐與應(yīng)用，讓學(xué)生在活動(dòng)中提取信息、整理數(shù)據(jù)，并用數(shù)學(xué)的方法推理證明，由簡(jiǎn)到繁，逐層推進(jìn).

由此可見(jiàn)，情境教學(xué)更有利于構(gòu)建邏輯思維的層序性、適應(yīng)性與靈活性，也更有利于學(xué)生潛移默化地獲取新知識(shí)并內(nèi)化為素養(yǎng)，讓學(xué)生體會(huì)到數(shù)學(xué)來(lái)源于實(shí)踐活動(dòng).

3 驅(qū)動(dòng)探疑的激情，交流建模的感悟

“問(wèn)題串”將課程內(nèi)容、教學(xué)過(guò)程和課程目標(biāo)合為一體，江蘇省的中考試題也淋漓盡致地體現(xiàn)了這一舉措.課堂教學(xué)目的之一在于發(fā)展學(xué)生存疑、探疑和釋疑的能力，因此，“問(wèn)題串”作為教學(xué)的核心，是師生展示探究活動(dòng)的基本點(diǎn).

案例3 肖老師在講授“四邊形的性質(zhì)”的復(fù)習(xí)課時(shí)，課堂實(shí)錄片段如下：

投影：閱讀材料——通過(guò)認(rèn)識(shí)一個(gè)事物的局部或其特殊類型，可以逐步認(rèn)識(shí)這個(gè)事物.比如通過(guò)學(xué)習(xí)兩類特殊的四邊形，即平行四邊形和梯形來(lái)逐步認(rèn)識(shí)四邊形.

活動(dòng)：分別繪出一個(gè)平行四邊形和一個(gè)梯形.繪制的原則是什么？

引導(dǎo)：對(duì)于一種特殊四邊形的學(xué)習(xí)，一般先學(xué)習(xí)圖形的定義，再探索發(fā)現(xiàn)其性質(zhì)和判定方法，然后通過(guò)解決簡(jiǎn)單的問(wèn)題鞏固所學(xué)知識(shí).

投影：如圖6，把滿足AB=AD，CB=CD且AB≠BC的四邊形ABCD叫做“箏形”.

解決問(wèn)題：

（1）寫出箏形除定義外的兩個(gè)性質(zhì)；

（2）寫出箏形除定義外的兩個(gè)判定方法，并選出一個(gè)進(jìn)行證明.（活動(dòng)為自主、交流.）

評(píng)價(jià)：肖老師的這節(jié)課是以“箏形”定義對(duì)特殊四邊形進(jìn)行的一種拓展.學(xué)生可以通過(guò)“做一做、議一議、悟一悟”來(lái)探疑和釋疑.創(chuàng)設(shè)的質(zhì)疑情境具有開放性，目的是通過(guò)學(xué)生得出結(jié)論的展示和交流，激發(fā)學(xué)生思維的碰撞，促使學(xué)生對(duì)探疑和釋疑過(guò)程進(jìn)行反思與歸納，梳理整合探究活動(dòng)中與特殊四邊形相關(guān)的數(shù)學(xué)知識(shí)點(diǎn)，系統(tǒng)發(fā)展學(xué)生的數(shù)學(xué)學(xué)科綜合素養(yǎng)，形成數(shù)學(xué)思想.

總之，課堂教學(xué)模式應(yīng)與學(xué)生學(xué)習(xí)模式同步，產(chǎn)生共振，其核心就是營(yíng)造學(xué)習(xí)氛圍.“情境+問(wèn)題串”教學(xué)模式是在教學(xué)理論指導(dǎo)下課堂教學(xué)實(shí)踐的結(jié)晶，該教學(xué)模式能夠助力學(xué)生學(xué)科素養(yǎng)的構(gòu)建.

參考文獻(xiàn)：

［1］張潔，劉毅.妙用“問(wèn)題串”破難點(diǎn) 巧借“情境”提素養(yǎng)——“相似圖形”教學(xué)舉隅［J］.數(shù)學(xué)教學(xué)通訊，2021（23）：6-8.

［2］李金霞.發(fā)揮教材中情境的價(jià)值 引領(lǐng)數(shù)學(xué)學(xué)習(xí)全過(guò)程［J］.遼寧教育，2021（17）：76-79.

［3］張艷萍，王利.問(wèn)題“串”起認(rèn)知過(guò)程 學(xué)生“卷”入深度學(xué)習(xí)——以“什么是周長(zhǎng)”一課為例［J］.黑龍江教育（教育與教學(xué)），2022（8）：34-37.