建構(gòu)深度教學(xué)　凸顯核心素養(yǎng)

黃慶福　鄭林

摘要：數(shù)學(xué)核心素養(yǎng)的培養(yǎng)要求教師在傳授學(xué)生知識(shí)的過程中提升學(xué)生解決問題的能力以及推理的能力.深度教學(xué)作為培育核心素養(yǎng)的重要載體，需要引起我們的重視.教師的深度教學(xué)是學(xué)生深度學(xué)習(xí)的前提，學(xué)生的深度學(xué)習(xí)是深度教學(xué)要達(dá)成的目標(biāo)，二者有機(jī)結(jié)合、相輔相成.

關(guān)鍵詞：核心素養(yǎng)；問題引領(lǐng)；深度教學(xué)

教育部印發(fā)的《關(guān)于全面深化課程改革落實(shí)立德樹人根本任務(wù)的意見》中明確提出全面深化課程改革以及核心素養(yǎng)在各學(xué)科間落地開花的要求.在數(shù)學(xué)學(xué)科中，核心素養(yǎng)更多的是指以數(shù)學(xué)為工具解決實(shí)際問題的能力.這種能力的提高可以通過深度教學(xué)來實(shí)現(xiàn).所謂深度教學(xué)，就是對知識(shí)進(jìn)行深層剖析，了解知識(shí)間的縱橫交錯(cuò)，提高思維的深度和廣度，同時(shí)帶動(dòng)具體思維向邏輯思維的縱深發(fā)展.

深度教與學(xué)的落實(shí)，需要教師帶領(lǐng)學(xué)生建構(gòu)完整的知識(shí)體系，激發(fā)學(xué)生的邏輯思維，將所學(xué)知識(shí)靈活運(yùn)用到解題過程中.本文中以直角三角形的性質(zhì)定理為例，闡述如何在課堂上基于核心素養(yǎng)視角重新審視知識(shí)，構(gòu)建深度的教與學(xué).

1 問題引領(lǐng)，深度課堂

1.1 教學(xué)有疑，疑則有進(jìn)

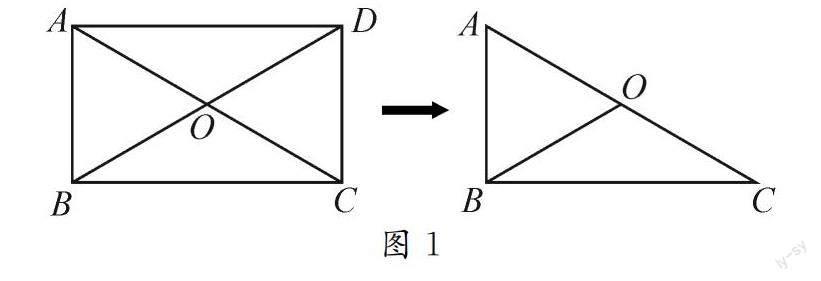
人教版教材中關(guān)于直角三角形斜邊上中線的性質(zhì)定理安排在八年級下冊“18.2.1矩形”中.在講解完矩形的性質(zhì)之后，提出問題：如圖1，在矩形ABCD中，觀察Rt△ABC，BO是斜邊AC上的中線，BO與AC有什么關(guān)系^［1］？

教材中這樣安排新定理的生成是基于矩形的四個(gè)角均為直角，因此自然想到借助矩形研究直角三角形中的問題.如此安排雖利于知識(shí)生成但不利于知識(shí)發(fā)展，且不利于學(xué)生思維能力的培養(yǎng)，無法激發(fā)學(xué)生的求知欲.

1.2 知識(shí)的問題化

本文中在深入探究該定理教學(xué)的同時(shí)，結(jié)合可以關(guān)聯(lián)的知識(shí)，引導(dǎo)學(xué)生構(gòu)建數(shù)學(xué)知識(shí)的整個(gè)脈絡(luò)圖，學(xué)會(huì)用聯(lián)系的思維看知識(shí)，用發(fā)展的眼光看數(shù)學(xué).學(xué)生經(jīng)歷以上過程，進(jìn)而對所學(xué)知識(shí)做到真正理解，并逐步構(gòu)建數(shù)學(xué)知識(shí)框架和體系.

問題 求證：直角三角形斜邊上的中線等于斜邊的一半.

已知：如圖2，在Rt△ABC中，∠ABC=90°，D是斜邊AC的中點(diǎn)，連接BD.

求證：BD=?AC.

問題1 猜測BD與AC之間有什么數(shù)量關(guān)系？

問題2 能通過折線來驗(yàn)證你的猜想嗎？

學(xué)生經(jīng)過思考和交流，利用圖3的折疊方法，可驗(yàn)證猜想.

2 多向思維，助力推理

上述問題打開了深度教學(xué)的大門，而測量和折紙降低了進(jìn)入的門檻，讓學(xué)生“觸手可得”.另外，折紙還蘊(yùn)含著軸對稱的特性，教師引導(dǎo)學(xué)生關(guān)注知識(shí)的內(nèi)涵，從而獲得多角度的論證方法.

證法一：論證角度——建構(gòu)矩形模型.

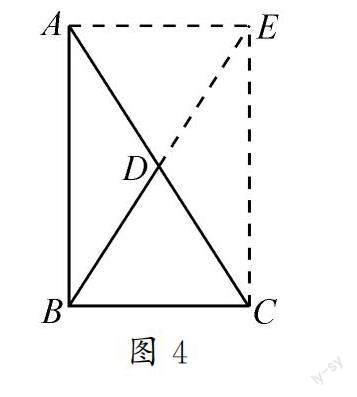
證明：如圖4，延長BD至點(diǎn)E，使ED=DB，連接CE，AE.

∵D為AC的中點(diǎn)，

∴AD=CD.

∵BD=DE，

∴四邊形ABCE為平行四邊形.

∵∠ABC=90°，

∴四邊形ABCE為矩形.

∴AC=BE.

又BD=?BE，

∴BD=?AC.

證法二：論證角度——建構(gòu)等角對等邊.

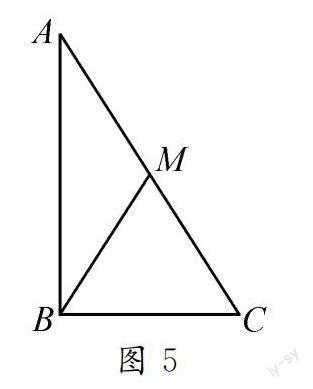
證明：如圖5，在∠ABC的內(nèi)部作∠MBC=∠C，BM與AC交于點(diǎn)M.

∵∠MBC=∠C，

∴MB=MC.

∵∠ABC=90°，

∴∠A+∠C=90°，

∠ABM+∠MBC=90°.

∴∠A=∠ABM.

∴AM=BM.

∴AM=MC=BM.

即BM是斜邊AC上的中線，且BM=?AC.

又BD是斜邊AC上的中線，即BD與BM重合.

∴BD=?AC.

證法三：論證角度——建構(gòu)三角形中位線，引出中垂線.

證明：如圖6，在△ABC中，∠ABC=90°，BD為AC邊上的中線，分別取AB，BC的中點(diǎn)G，H，連結(jié)DG，DH.

∵AD=DC，AG=GB，

∴DG∥BC.

∵∠ABC=90°，

∴∠AGD=∠ABC=90°.

∴DG⊥AB.

又AG=BG，

∴BD=AD.

同理BD=CD.

∴AD=BD=CD.

∴BD=?AC.

證法四：論證角度——建構(gòu)三角形全等.

證明：如圖7，延長BD至點(diǎn)E，使BD=DE，連接EC.

易證△ADB≌△CDE（SAS）.

∴∠A=∠1，AB=CE.

∴AB∥EC.

∴∠ABC+∠BCE=180°.

∵∠ABC=90°，

∴∠BCE=90°.

易證△ABC≌△ECB（SAS）.

∴AC=BE.

∵BD=?BE，

∴BD=?AC.

證法五：論證角度——構(gòu)造中垂線以及聯(lián)想等角對等邊.

證明：如圖8，作AB的垂直平分線ME，垂足為E，交AC于點(diǎn)M.連接BM，則AM=BM.

∴∠1=∠A.

∵∠ABC=90°，

∴∠3+∠1=90°，

∠2+∠A=90°.

∴∠3=∠2.

∴CM=BM.

∵AM=BM，

∴CM=AM.

即M為AC的中點(diǎn).

又D為AC的中點(diǎn)，

∴點(diǎn)M與點(diǎn)D重合.

∴BD=AD=CD.

即BD=?AC.

證法六：論證角度——由中點(diǎn)聯(lián)想中位線.

證明：如圖9，延長CB至點(diǎn)E，使BE=BC，連接AE.

則B為EC的中點(diǎn).

∵D為AC的中點(diǎn)，

∴BD為△ACE的一條中位線.

∴BD=?AE.

∵∠ABC=90°，

∴AB⊥BC.

∵BE=BC，

∴AE=AC.

∴BD=?AC.

3 逆向思維，合作探究

在進(jìn)行命題的學(xué)習(xí)時(shí)，探究逆命題的過程能讓深度教學(xué)內(nèi)容更豐富，并能提升學(xué)生的推理能力^［2］.通過逆命題的證明，培養(yǎng)學(xué)生的逆向思維能力，同時(shí)又將知識(shí)遷移到“命題、定理、證明”這一課時(shí)中，增加了知識(shí)的層次.

問題3 “直角三角形斜邊上的中線等于斜邊的一半”的逆命題的題設(shè)和結(jié)論分別是什么？

問題4 這個(gè)逆命題是否成立？說明理由.

4 應(yīng)用新知，固化認(rèn)識(shí)

例題 如圖10，已知等腰直角三角形ABC與等腰直角三角形BDF，∠BAC=∠BDF=90°，E是線段CF的中點(diǎn).

（1）如圖10，當(dāng)點(diǎn)B，C，D在同一直線上時(shí)，猜想線段AE與DE的數(shù)量關(guān)系和位置關(guān)系，并證明；

（2）如圖11、圖12，當(dāng)點(diǎn)B，C，D不在同一直線上，且等腰直角三角形ABC與等腰直角三角形BDF在BC的同側(cè)或異側(cè)時(shí)，探究線段AE與DE的數(shù)量關(guān)系和位置關(guān)系；

本題第（1）問直接運(yùn)用本節(jié)所學(xué)的直角三角形的性質(zhì)定理.在Rt△AFC與Rt△DFC中你能得到什么結(jié)論？第（2）問顯然不存在Rt△AFC與Rt△DFC，但是以上三個(gè)圖形中都存在等腰直角三角形ABC與等腰直角三角形BDF.等腰三角形有一個(gè)“三線合一”的重要性質(zhì)，教師結(jié)合本節(jié)所學(xué)的直角三角形的性質(zhì)定理，引導(dǎo)學(xué)生添加輔助線解決第（1）問.

如圖13，分別取BF與BC的中點(diǎn)N與M，連接DN，NE，ME，AM.進(jìn)一步引導(dǎo)學(xué)生觀察圖形，找出三角形的中位線，則可證△AME≌△END（SAS）且AM⊥NE，因此可證DE=AE且DE⊥AE.

接下來，引導(dǎo)學(xué)生關(guān)注圖形的運(yùn)動(dòng)變化過程中不變的量，將第（1）問添加輔助線的思路遷移到圖11與圖12中，鼓勵(lì)學(xué)生大膽嘗試，畫圖驗(yàn)證，得到圖14與圖15.

此題的變式訓(xùn)練，能讓學(xué)生的思維得到進(jìn)一步拓展，同時(shí)明確某些證明題的設(shè)計(jì)理念，即對題目的條件或基本圖形進(jìn)行變換.

5 深度教與學(xué)的走向：傳遞知識(shí)，更傳遞智慧

5.1 有一種教學(xué)叫：觸類旁通

作為課堂的組織者，我們要站在一定的高度來看待知識(shí)，領(lǐng)會(huì)教材編者的意圖，不斷改進(jìn)教材教法，遵循吃透教材—改編教材—拓展教材這一過程，學(xué)會(huì)用聯(lián)系的觀點(diǎn)來看待教材，挑選典型例題，分析通法通性.讓學(xué)生學(xué)會(huì)融會(huì)貫通.

5.2 有一種學(xué)習(xí)叫：深入淺出

教師在備課時(shí)要多花時(shí)間思考“如何實(shí)現(xiàn)知識(shí)的深入和教法的淺出”.課堂上我們不能“裝高深”，應(yīng)該“接地氣”，用學(xué)生熟悉的已知情境、事物和知識(shí)來牽引.教師每拋出一個(gè)問題，都要從最簡單的角度入手，步步深入，從特殊到一般.

5.3 有一種智慧叫：大道至簡

深度教與學(xué)中，教師要做的是基于教材本身，選取適當(dāng)素材，課堂上重視探究過程.常言道：經(jīng)歷過程比結(jié)論更重要，知識(shí)可以在探索過程中生根發(fā)芽；大道至簡，知易行難.

6 是結(jié)尾也是開端

數(shù)學(xué)深度教與學(xué)是一個(gè)雙向過程，也是一個(gè)雙贏的結(jié)局.深度教與學(xué)作為培養(yǎng)學(xué)生核心素養(yǎng)的重要途徑，還需要我們在實(shí)踐中繼續(xù)豐富和探索.深度教與學(xué)幫助學(xué)生成為可持續(xù)發(fā)展的人才，讓學(xué)生在今后的學(xué)習(xí)、生活和工作中能用數(shù)學(xué)的眼光來看待世界，用數(shù)學(xué)的思維來解決問題，從而達(dá)成目標(biāo)，實(shí)現(xiàn)自我價(jià)值.

參考文獻(xiàn)：

［1］人民教育出版社，課程教材研究所，中學(xué)數(shù)學(xué)課程教材研究開發(fā)中心.義務(wù)教育教科書教師教學(xué)用書＼5數(shù)學(xué)＼5八年級＼5下冊［M］.北京：人民教育出版社，2019：101.

［2］高旻.基于“深度教學(xué)”提升推理能力——“直角三角形的性質(zhì)定理”的教學(xué)與思考［J］.中學(xué)數(shù)學(xué)月刊，2020（9）：31-33.