借助數(shù)線教學(xué),發(fā)展核心素養(yǎng)
陳蒨 陸世奇 徐文彬

【摘? ?要】數(shù)線即表征數(shù)的意義、性質(zhì)和運(yùn)算的線,在小學(xué)數(shù)學(xué)教學(xué)中有著廣泛的應(yīng)用。小學(xué)數(shù)學(xué)中,常見的數(shù)線除了具有嚴(yán)格性和結(jié)構(gòu)性的數(shù)軸,還有其他類型。充分運(yùn)用各種數(shù)線展開教學(xué),有助于實(shí)現(xiàn)數(shù)形結(jié)合,促進(jìn)學(xué)生核心素養(yǎng)的培養(yǎng)。具體來(lái)說(shuō),依托數(shù)線認(rèn)數(shù),可以發(fā)展學(xué)生的數(shù)感;巧借數(shù)線運(yùn)算,可以發(fā)展學(xué)生的運(yùn)算能力;活用數(shù)線分析,可以發(fā)展學(xué)生的幾何直觀。
【關(guān)鍵詞】數(shù)線;核心素養(yǎng);數(shù)感;運(yùn)算能力;幾何直觀
數(shù)線即表征數(shù)的意義、性質(zhì)和運(yùn)算的線。數(shù)線在小學(xué)數(shù)學(xué)教學(xué)中有著廣泛的應(yīng)用。其中,應(yīng)用最廣泛、最特殊的數(shù)線就是數(shù)軸。數(shù)軸是一條帶有原點(diǎn)、正方向和單位長(zhǎng)度的直線,一些研究者也將其稱為結(jié)構(gòu)化數(shù)線。[1]除數(shù)軸外,“數(shù)線家族”還有很多其他成員,如心理數(shù)線、空數(shù)線、雙數(shù)線等。在教學(xué)中,教師可以根據(jù)不同的問(wèn)題情境和學(xué)習(xí)需求呈現(xiàn)不同類型的數(shù)線,實(shí)現(xiàn)數(shù)形結(jié)合。
在教學(xué)中,以數(shù)軸為主,輔以其他類型的數(shù)線,可以為學(xué)生理解數(shù)學(xué)知識(shí)、發(fā)展核心素養(yǎng)提供更多機(jī)會(huì)。基于此,筆者試探究數(shù)線在小學(xué)階段的應(yīng)用,包括在數(shù)的認(rèn)識(shí)、數(shù)的運(yùn)算及解決問(wèn)題等多個(gè)維度上的教學(xué)實(shí)踐,為培養(yǎng)學(xué)生的數(shù)感、運(yùn)算能力和幾何直觀等核心素養(yǎng)助力。
一、依托數(shù)線認(rèn)數(shù),發(fā)展學(xué)生數(shù)感
數(shù)線是認(rèn)數(shù)的直觀工具,數(shù)線可以幫助學(xué)生理解數(shù)的意義、認(rèn)識(shí)數(shù)的順序、厘清數(shù)的關(guān)系。《義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2022年版)》(以下簡(jiǎn)稱《課程標(biāo)準(zhǔn)》)指出,數(shù)感主要是指對(duì)于數(shù)與數(shù)量、數(shù)量關(guān)系及運(yùn)算結(jié)果的直觀感悟,包括能夠理解數(shù)的意義、能用數(shù)表示物體的個(gè)數(shù)或事物的順序、能進(jìn)行合理的估算。[2]依托數(shù)線開展認(rèn)數(shù)教學(xué),有助于學(xué)生數(shù)感的發(fā)展。
(一)以數(shù)線為主線貫穿認(rèn)數(shù)教學(xué)
對(duì)小學(xué)數(shù)學(xué)教材進(jìn)行梳理,不難發(fā)現(xiàn),數(shù)線出現(xiàn)在每一個(gè)有關(guān)認(rèn)數(shù)的教學(xué)單元中。以蘇教版小學(xué)數(shù)學(xué)教材為例,數(shù)線就出現(xiàn)在了認(rèn)識(shí)10以內(nèi)的數(shù)、認(rèn)識(shí)11~20各數(shù)、認(rèn)識(shí)100以內(nèi)的數(shù)、認(rèn)識(shí)萬(wàn)以內(nèi)的數(shù)、認(rèn)識(shí)多位數(shù),以及認(rèn)識(shí)小數(shù)、分?jǐn)?shù)、負(fù)數(shù)等教學(xué)單元。這說(shuō)明教師要用好數(shù)線這一直觀教學(xué)工具,以整體性、結(jié)構(gòu)化的思路來(lái)設(shè)計(jì)教學(xué),使學(xué)生在每一階段都能循序漸進(jìn)地理解數(shù)的意義、認(rèn)識(shí)數(shù)的順序、厘清數(shù)的關(guān)系。特別是在認(rèn)識(shí)小數(shù)、分?jǐn)?shù)及負(fù)數(shù)時(shí),借助數(shù)軸能幫助學(xué)生自然理解數(shù)系的擴(kuò)張,逐漸建構(gòu)自身的數(shù)系認(rèn)知網(wǎng)絡(luò)。[3]
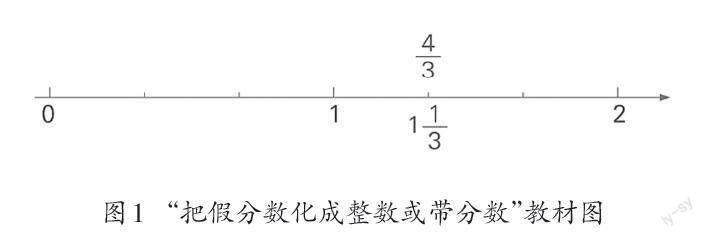
例如,蘇教版教材五年級(jí)下冊(cè)“把假分?jǐn)?shù)化成整數(shù)或帶分?jǐn)?shù)”的教學(xué)內(nèi)容中,以數(shù)形結(jié)合的形式呈現(xiàn)了[43](如圖1)。教材編排的意圖在于引導(dǎo)學(xué)生把假分?jǐn)?shù)化成整數(shù)或帶分?jǐn)?shù),并表示在數(shù)線上,從而幫助學(xué)生深入理解分?jǐn)?shù)的意義、建立分?jǐn)?shù)與整數(shù)的內(nèi)在關(guān)系,實(shí)現(xiàn)數(shù)系的自然擴(kuò)張。這種依托數(shù)線認(rèn)識(shí)分?jǐn)?shù)的教學(xué)方式,有助于學(xué)生直觀地理解分?jǐn)?shù)的意義、厘清分?jǐn)?shù)與整數(shù)的關(guān)系,從而把分?jǐn)?shù)正確納入自身已有的數(shù)系結(jié)構(gòu)中。當(dāng)然,這一教學(xué)方式的實(shí)施必須基于教師對(duì)認(rèn)數(shù)教學(xué)整體性和結(jié)構(gòu)性的把握,以及學(xué)生長(zhǎng)期以來(lái)積累的對(duì)數(shù)線的認(rèn)知經(jīng)驗(yàn)。如果每一次的認(rèn)數(shù)教學(xué)都能依托數(shù)線來(lái)幫助學(xué)生建立對(duì)數(shù)的理解,那么每一次數(shù)系的擴(kuò)張對(duì)學(xué)生來(lái)說(shuō)就是自然而然、順理成章的了。
值得注意的是,學(xué)生在認(rèn)識(shí)數(shù)的同時(shí)也在學(xué)習(xí)數(shù)線相關(guān)的知識(shí),同時(shí)形成物理意義和心理意義上的數(shù)線。心理數(shù)線是個(gè)人在腦海中構(gòu)造的數(shù)線,是學(xué)生在學(xué)習(xí)物理數(shù)線過(guò)程中的一種內(nèi)化。心理數(shù)線的發(fā)展,與測(cè)量、分類等數(shù)學(xué)能力的發(fā)展似乎是齊頭并進(jìn)的。[4]這是數(shù)感發(fā)展的體現(xiàn),也是數(shù)感外顯的表現(xiàn)形式之一,即學(xué)生能夠基于心理數(shù)線自主建構(gòu)物理數(shù)線。因此,教師可以讓學(xué)生運(yùn)用無(wú)界數(shù)線(如圖2)和空數(shù)線(如圖3)來(lái)“造數(shù)”。
(二)以數(shù)線為支點(diǎn)突破近似數(shù)難點(diǎn)
能進(jìn)行合理的估計(jì)、估算也是數(shù)感的具體表現(xiàn)之一。用“四舍五入法”取近似數(shù)是認(rèn)數(shù)教學(xué)的一個(gè)難點(diǎn)。以蘇教版教材為例,在四年級(jí)下冊(cè)“認(rèn)識(shí)多位數(shù)”單元“近似數(shù)的認(rèn)識(shí)”的教學(xué)中,認(rèn)識(shí)大數(shù)對(duì)學(xué)生來(lái)說(shuō)較為困難,用“四舍五入法”求一個(gè)數(shù)的近似數(shù)就更難了。從教材的主題圖(如圖4)可以看出,數(shù)線是突破這一難點(diǎn)的有效支架。“近似數(shù)的認(rèn)識(shí)”常常面臨教師施教“重法輕理”、學(xué)生學(xué)習(xí)“知其然而不知其所以然”的困境。數(shù)線的有效利用能打破這一僵局,使得教師教學(xué)“理法并舉”,學(xué)生學(xué)習(xí)“融會(huì)貫通”。
解答圖4中的問(wèn)題,需把男性人數(shù)384204和女性人數(shù)386685對(duì)應(yīng)的大致位置標(biāo)在數(shù)線上。這涉及兩種學(xué)生可能使用的數(shù)線估計(jì)模型:線性模型與對(duì)數(shù)模型。線性模型指?jìng)€(gè)體對(duì)所有數(shù)字的表征具有相等的心理空間距離,相鄰數(shù)字之間的距離不會(huì)因數(shù)量的增加而改變。[5]對(duì)數(shù)模型則是指,對(duì)于某一范圍內(nèi)的數(shù)字,個(gè)體傾向于擴(kuò)大低端數(shù)字間的距離而縮小高端數(shù)字間的距離。[6]如在0~1000范圍內(nèi),個(gè)體在心理上會(huì)認(rèn)為1與75的距離比75與1000的距離要大。
在數(shù)線上標(biāo)數(shù)的過(guò)程,不僅是一個(gè)操作過(guò)程,也是一個(gè)對(duì)數(shù)及其關(guān)系的理解過(guò)程,更是對(duì)數(shù)線的感知過(guò)程。學(xué)生在標(biāo)數(shù)任務(wù)中出錯(cuò),原因可能在于運(yùn)用了錯(cuò)誤的數(shù)線估計(jì)策略。開展變式訓(xùn)練是一種可能的教學(xué)手段。教材中呈現(xiàn)的是一種半結(jié)構(gòu)化的數(shù)線(在38萬(wàn)到39萬(wàn)之間有單位,但未顯示單位長(zhǎng)度),其變式既可以增加單位長(zhǎng)度,也可以去除單位,從而讓學(xué)生在各種數(shù)線情境下標(biāo)數(shù),以呈現(xiàn)他們對(duì)數(shù)線的理解情況。教師據(jù)此引導(dǎo)學(xué)生形成恰當(dāng)?shù)臄?shù)線估計(jì)(標(biāo)數(shù))策略,可以促進(jìn)學(xué)生對(duì)近似數(shù)的理解,有助于學(xué)生生成對(duì)數(shù)的估計(jì)的感悟,逐步內(nèi)化對(duì)數(shù)的大小和近似數(shù)的感知,從而發(fā)展數(shù)感。
二、巧借數(shù)線運(yùn)算,發(fā)展學(xué)生運(yùn)算能力
數(shù)線有利于發(fā)展學(xué)生的運(yùn)算能力。它可以呈現(xiàn)運(yùn)算過(guò)程,讓學(xué)生更直觀地感受運(yùn)算過(guò)程。在這個(gè)過(guò)程中,學(xué)生既可以借助數(shù)線感知運(yùn)算間的關(guān)聯(lián),也可以借助數(shù)線理解運(yùn)算的意義。
(一)借助數(shù)線感知運(yùn)算間的關(guān)聯(lián)
對(duì)于小學(xué)生而言,感知運(yùn)算之間的關(guān)聯(lián)是非常困難的。尤其是低年級(jí)的學(xué)生,他們對(duì)運(yùn)算的理解是孤立的,加法是加法,減法是減法,很難理解加減法之間的關(guān)系。借助數(shù)線,可以幫助學(xué)生直觀感知加法和減法之間的關(guān)聯(lián),初步認(rèn)識(shí)減法是加法的逆運(yùn)算。
例如,浙教版教材一年級(jí)上冊(cè)在“練一練八”中安排了圖5的練習(xí)題,借助數(shù)線來(lái)幫助一年級(jí)學(xué)生理解加減法之間的聯(lián)系。圖5中的數(shù)線具有正方向,箭頭方向與正方向相同是加,箭頭方向與正方向相反則是減。把兩幅圖放在一起理解,能幫助學(xué)生直觀感知加減法的相同點(diǎn)和不同點(diǎn),感悟加減法的本質(zhì)是相同的,理解減法是加法的逆運(yùn)算。當(dāng)然,教師進(jìn)行教學(xué)設(shè)計(jì)時(shí),必須注意一年級(jí)學(xué)生的數(shù)線經(jīng)驗(yàn),如他們對(duì)正方向和單位長(zhǎng)度的理解程度。
(二)借助數(shù)線理解運(yùn)算的意義
四則運(yùn)算的意義是理解算理、探索算法、分析數(shù)量關(guān)系的基礎(chǔ),也是四則運(yùn)算內(nèi)容的核心[7],對(duì)學(xué)生運(yùn)算能力的發(fā)展至關(guān)重要。在運(yùn)算教學(xué)中,巧妙借助數(shù)線能幫助學(xué)生理解運(yùn)算的意義。
以蘇教版教材為例,二年級(jí)上冊(cè)“表內(nèi)乘法(一)”單元“5的乘法口訣”這一內(nèi)容的“想想做做”中,就出現(xiàn)了用數(shù)線表示乘法意義的練習(xí)題(如圖6)。乘法的本質(zhì)意義是幾個(gè)相同加數(shù)的和(幾個(gè)幾相加)的簡(jiǎn)便運(yùn)算,也就是等距連加。像圖6這樣把乘法的意義形象地表示為在數(shù)線上連跳,不僅富有童趣,還有助于學(xué)生對(duì)乘法意義的直觀理解。此處的變式可以采用無(wú)界數(shù)線(如在數(shù)線上僅顯示到10),讓學(xué)生繼續(xù)補(bǔ)充單位,在理解數(shù)線結(jié)構(gòu)的基礎(chǔ)上形成對(duì)乘法的理解。
三、活用數(shù)線分析,發(fā)展學(xué)生幾何直觀
數(shù)線是一種非常重要的直觀模型,在解決問(wèn)題中也發(fā)揮著重要的作用。數(shù)線上的數(shù)從小到大排列,形成一段一段的區(qū)間。教師充分利用數(shù)線的區(qū)間性與等分性,可以巧妙地解決許多數(shù)學(xué)問(wèn)題。[8]
(一)靈活運(yùn)用數(shù)線表征時(shí)間問(wèn)題
計(jì)算經(jīng)過(guò)時(shí)間是一個(gè)教學(xué)難點(diǎn)。靈活運(yùn)用數(shù)線來(lái)呈現(xiàn)時(shí)間軸,能有效幫助學(xué)生突破難點(diǎn),理解計(jì)算經(jīng)過(guò)時(shí)間的本質(zhì)。以蘇教版教材為例,“計(jì)算經(jīng)過(guò)時(shí)間”這一內(nèi)容安排在三年級(jí)下冊(cè)“年、月、日”教學(xué)單元,主題圖和時(shí)間軸如圖7所示。
從圖7可以看出,用數(shù)線表征的時(shí)間軸非常形象,能幫助學(xué)生直觀把握開始時(shí)間、結(jié)束時(shí)間以及經(jīng)過(guò)時(shí)間三者之間的關(guān)系,為學(xué)生搭建可視化的支架,突破教學(xué)難點(diǎn)。同時(shí)也能幫助學(xué)生建立直觀模型,把抽象的時(shí)間問(wèn)題變得直觀、形象,從而發(fā)展學(xué)生的幾何直觀。
(二)創(chuàng)新運(yùn)用數(shù)線解決分段問(wèn)題
分段問(wèn)題在日常生活中應(yīng)用廣泛,如電費(fèi)、水費(fèi)、出租車收費(fèi)、停車費(fèi)等的分段計(jì)費(fèi)。對(duì)學(xué)生而言,分段問(wèn)題呈現(xiàn)的信息較多,解決問(wèn)題的過(guò)程比較復(fù)雜。借助數(shù)線模型能幫助學(xué)生直觀理解分段的具體情況,厘清數(shù)量間的關(guān)系,進(jìn)而解決問(wèn)題。
例如,人教版教材五年級(jí)上冊(cè)“小數(shù)乘法”教學(xué)單元中的“小數(shù)乘法解決問(wèn)題”就是一個(gè)出租車收費(fèi)的分段問(wèn)題(如圖8)。學(xué)生雖然能理解題意,但由于缺少分段討論的經(jīng)驗(yàn),他們對(duì)收費(fèi)標(biāo)準(zhǔn)并不是很清楚。因此,教師要適時(shí)引導(dǎo)學(xué)生用數(shù)線模型(如圖9)來(lái)表征這個(gè)復(fù)雜的問(wèn)題,架起數(shù)與量之間的橋梁,幫助學(xué)生直觀理解分段計(jì)費(fèi)的規(guī)則,發(fā)展幾何直觀,積累解決復(fù)雜問(wèn)題的經(jīng)驗(yàn)。
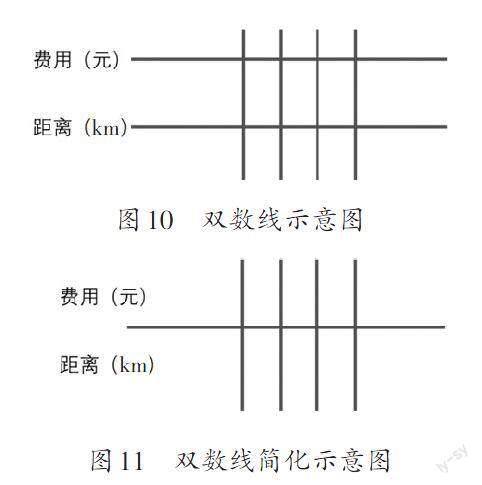
教師還可以設(shè)計(jì)變式練習(xí),讓學(xué)生為半結(jié)構(gòu)化的雙數(shù)線(即兩條數(shù)線聯(lián)結(jié),如圖10、圖11)補(bǔ)充信息,從而厘清數(shù)量關(guān)系。
綜上所述,數(shù)線是小學(xué)數(shù)學(xué)學(xué)習(xí)的一個(gè)有效載體,在培養(yǎng)學(xué)生數(shù)感、運(yùn)算能力、幾何直觀等核心素養(yǎng)方面發(fā)揮著舉足輕重的作用。除了數(shù)軸,在教學(xué)中還可以運(yùn)用數(shù)線家族中其他各種形式的數(shù)線,充分發(fā)揮數(shù)線的價(jià)值。
參考文獻(xiàn):
[1]WONG M. Identifying fractions on a number line[J]. Australian primary mathematics classroom,2013,18(3):13-18.
[2]中華人民共和國(guó)教育部.義務(wù)教育數(shù)學(xué)課程標(biāo)準(zhǔn)(2022年版)[M].北京:北京師范大學(xué)出版社,2022:7.
[3]姚建法.數(shù)軸:“真是一條神奇的線”[J].教學(xué)月刊·小學(xué)版(數(shù)學(xué)),2019(7/8):58-60.
[4]ZANG B,ZHANG J,GU R. Chinese preschoolers mental number line and mental number distance:valid characteristics using dirichlet process gaussian mixture model[J]. Early education and development,2019,30(5):694-707.
[5]CASE R,SOWDER J T. The development of computational estimation:a neo-Piagetian analysis[J]. Cognition and instruction,1990,7(2):79-104.
[6]DEHAENE S. The number sense:how the mind creates mathematics[M].New York:Oxford University Press,1997:53-76.
[7]張莎莎.用好數(shù)軸資源 發(fā)展數(shù)學(xué)思維[J].小學(xué)數(shù)學(xué)教育,2020(22):24-25.
[8]陳險(xiǎn)峰.巧借數(shù)軸 提升數(shù)感[J].新教師,2017(11):57-58.
(1.南京師范大學(xué)課程與教學(xué)研究所
2.江蘇省常州市武進(jìn)區(qū)實(shí)驗(yàn)小學(xué))

