NAEP四年級數學“測量”試題分析

高夢雅 林子植

【摘? ?要】小學階段作為系統學習測量知識的初級階段，對培育學生的測量素養起著奠基作用。教師可借鑒國外的成功經驗，編制“測量”試題，培養學生的測量素養。為此，教師選取2005—2022年NAEP四年級的“測量”試題，從核心素養、思維模式、問題情境、表征方式四個維度對其進行統計和分析。據此得出，小學“測量”試題的編制需重視以下幾點：量感和其他素養協同考查，體現綜合性；試題貼近學生生活，體現應用性；加強逆向思維考查，體現發展性；優化表征方式，體現過程性。

【關鍵詞】NAEP；測量；試題表征；量感

一、引言

測量是聯系兒童世界和數學世界的重要組成部分，對兒童生活以及兒童素養的發展都具有重要作用［1］。小學階段作為系統學習測量知識的初級階段，對培育學生的測量素養起著奠基作用。綜觀國際數學課程內容可以發現，大部分國家都把“測量”作為一個單獨的學習板塊，或者以“測量”為主線開展學習，可見“測量”知識對學生發展的重要性。但是，我國義務教育階段的數學課程內容由數與代數、圖形與幾何、統計與概率、綜合與實踐四個學習領域組成［2］，小學數學測量知識分散在“圖形與幾何”“綜合與實踐”等多個領域，缺乏系統性。因此，我國可借鑒國外的成功經驗，思考如何編制“測量”試題，培養學生的測量素養。

美國國家教育進展評估項目（National Assessment of Educational Progress，以下簡稱“NAEP”）2019年小學四年級數學的評價框架，將小學數學內容劃分為數的性質與運算、測量、幾何、統計與概率以及代數五大領域，其占比分別為40%、20%、15%、10%、15%。評價框架明確指出，學生在測量領域應該掌握測量屬性和測量體系兩大內容，具體包括：能夠理解長度、溫度、時間、面積等測量屬性；能夠直接測量或估計測量大小、重量等物體屬性；能夠運用公式簡單計算圖形的面積或周長；能夠認識和理解單位且可以進行單位換算。那么，NAEP四年級的“測量”試題究竟是如何考查的，考查的內容有哪些特點？為此，筆者選取NAEP官網上已公布的2005—2022年四年級的“測量”試題，對其進行統計和分析，旨在為我國小學數學“測量”試題的編制提供借鑒和思考。

二、NAEP四年級數學“測量”試題分析

試題命制過程要兼顧立意、情境、設問和修飾，試題題干語言的表達要簡明準確，知識的考查要基于課程標準、聚焦核心素養，并注重數學思想方法［3］。因此，筆者選取2005—2022年NAEP已公布的55道小學數學四年級的“測量”試題，分別從核心素養、思維模式、問題情境、表征方式四個維度對其進行統計和分析。

（一）基于核心素養的試題分析

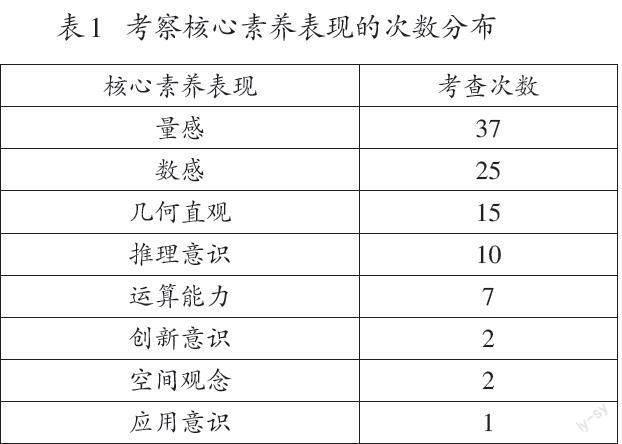
《義務教育數學課程標準（2022年版）》（以下簡稱《課程標準》）指出，試題命制應考查數學知識和核心素養的相應表現。因此，筆者以《課程標準》中的11個核心素養表現（如量感、數感等）為基礎，并咨詢多位專家及部分一線教師的意見，從考查核心素養表現的維度，對NAEP四年級“測量”試題進行了統計和分析（如表1）。

統計結果表明，從整體分布上看，55道“測量”試題一共考查了量感、數感、幾何直觀等8種核心素養表現，一道試題基本上考查了2～3種核心素養表現，主要偏重對量感、數感、幾何直觀等核心素養表現的考查；從關聯程度上看，大部分的試題在考查量感的同時，也考查了數感、幾何直觀等核心素養的表現。現以具體試題為例，來說明NAEP“測量”試題是如何考查學生的核心素養的。

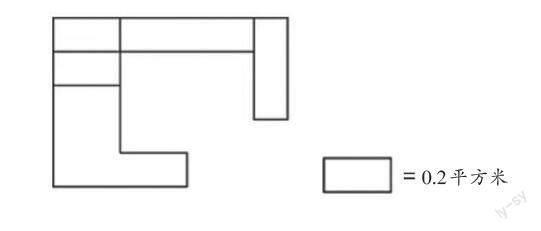
【試題1】（NAEP 2011年）估一估，此圖形的面積最可能是多少？

A.小于1平方米

B.大于1平方米，小于1.5平方米

C.大于1.5平方米，小于2.5平方米

D.大于2.5平方米

評析：這是一道單項選擇題，解題的思路是通過已知的圖形面積估測出未知的圖形面積，考查學生的量感、推理意識和幾何直觀的發展情況。估測圖形面積屬于量感的考查；由已知推斷未知屬于推理意識的考查；感知幾何圖形的大小及組成元素，建立數與形的聯系，計算圖形的大小，屬于幾何直觀的考查。

（二）基于思維模式的試題分析

培養學生的數學思維是數學教育的重中之重。數學課堂是培養數學思維的主要場所，思維能力評價對學生思維能力的形成起著重要的作用。從解題思維的方向出發，數學思維可以分為順向思維和逆向思維兩種思維模式。順向思維是指根據教材知識講解順序來思考問題，逆向思維是指通過反向方式思考問題。筆者依據這兩種思維模式，對NEAP四年級“測量”試題進行了統計和分析（如表2）。

統計結果表明：從整體上看，NAEP四年級“測量”試題以順向思維的考查為主，其考查了48次，逆向思維只考查了7次；從試題內容上看，逆向思維大多在測量屬性類試題中考查，主要從多角度考查學生對測量屬性的理解。下面借助試題2和試題3具體分析NAEP四年級“測量”試題是如何考查學生的思維模式的。

【試題2】（NAEP 2017年）下面哪個測量工具可以測量水的溫度？

A.鬧鐘? ?B.尺子? ?C.彈簧秤? ?D.溫度計

【試題3】（NAEP 2011年）這張圖在測量什么？

A.傳送包裹的時間? ?B.包裹的面積

C.包裹的長度? ? ? ? ? ?D.包裹的重量

評析：這兩道題是考查測量屬性和測量工具的問題。試題2的解題關鍵是學生要知道水的溫度是由特定的測量工具（溫度計）測量的，與教材中的知識講解思路相同，屬于順向思維類試題。試題3的解題關鍵在于學生要識別出圖中的測量工具（秤），且要清楚秤是用來測量物體重量的工具，屬于逆向思維試題。

（三）基于問題情境的試題分析

NAEP 2019小學四年級數學評估框架中明確指出，問題情境包括來源于學生熟悉的真實世界的現實情境和來源于數學學科的純數學情境，要努力尋求現實情境和純數學情境之間的平衡，從而達到豐富多樣的情境與具體數學知識的有機結合［4］。因此，筆者依據以上兩種情境，對NAEP四年級“測量”試題的問題情境設置進行了統計與分析（如表3）。

統計結果表明，在所統計的55道試題中，現實情境類試題有35道，占比63.6%；純數學情境類試題有20道，占比36.4%。為深入探析，現以具體試題為例進行說明。

【試題4】（NAEP 2013年）Kelly正穿著短袖T恤在外面玩，請估計現在外面的溫度可能是多少華氏度？（華氏度=32＋攝氏度×1.8）

A.0℉? ? ?B.32℉? ? ?C.85℉? ? D.212℉

評析：這道題考查學生對溫度的感知能力，通過Kelly的穿著推測溫度的高低，選擇比較合理的溫度。該題以身穿短袖T恤的Kelly在室外玩耍為背景，符合學生的認知水平，屬于現實情境的考查。把感知溫度放到現實情境中考查，使學生在解決問題的同時，加深對溫度高低的理解，提高推理意識。

（四）基于表征方式的試題分析

試題的表征方式影響學生讀取試題信息的準確性以及選擇解題策略的難易程度。因此，表征方式成為命題中不可忽視的影響因素。數學表征方式分為口頭表征、符號表征、圖表表征、多元表征（使用了兩種或三種表征形式的組合）四種［5］。筆者依據以上的分類方式，對NAEP四年級“測量”試題進行了統計和分析（如表4）。

統計結果表明，在55道試題中，用多元表征方式考查的次數最多，為24次，約占43.6%；沒有用符號表征考查的試題；用口頭表征方式考查的次數為18次，約占32.8%；用圖表表征方式考查的次數為13次，約占23.6%。現以具體試題進行深入分析，探究NAEP四年級“測量”試題是如何呈現的。

【試題5】（NAEP 2022年）Talat有一個罐子，他提出了三個和罐子有關的問題，下面哪個測量屬性可以回答Talat的問題，請把答案拖至對應的問題上。

【試題6】（NAEP 2011年）一本書的長度單位可能是什么？

A.厘米? ? ?B.米? ? ? C.平方厘米? ? ?D.平方米

評析：這兩道試題都在考查學生對測量工具、測量屬性及測量單位之間對應關系的判斷。不同的是，試題5是以具體的現實情境+圖表的形式呈現，屬于多元表征；試題6是以純文字形式呈現，要求學生根據問題的文字表述，找到相應的答案，屬于口頭表征。

三、思考與啟示

“測量”知識與生活應用息息相關，也是當今數學學科教材研究的焦點之一［6］。測量與日常生活、生產勞動以及科學研究有著密切的關系，能夠認識測量以及掌握測量的方法應該是每個公民必備的素養之一［7］。基于NAEP四年級“測量”試題的分析，結合《課程標準》的目標要求，筆者得出以下幾點啟示，為“測量”試題的編制提供參考。

（一）量感和其他素養協同考查，體現綜合性

《課程標準》在“命題原則”中明確指出，要堅持素養立意，凸顯育人導向。以核心素養為導向的考試命題，要關注數學的本質，關注通性通法，綜合考查“四基”“四能”與核心素養。一道試題中包含多個核心素養表現，有利于考查學生各個核心素養表現的發展情況，促進學生的全面發展。同時，也要注意，編制試題時，不應過分追求一道題中要考查的核心素養表現的個數，也不能刻意提高試題難度，增加學生的考試負擔。因此，未來我國編制“測量”試題時，需要關注各核心素養表現之間的關聯，合理安排核心素養表現的個數和難度水平，提高編制“測量”試題的水平。

（二）試題貼近學生生活，體現應用性

NAEP評估項目命題的特點之一是注重試題情境的真實性。將試題情境與學生實際生活聯系起來，有利于學生感受生活中的數學，體會數學的魅力，學會用數學思維思考問題。因此，“測量”試題的編制應該符合學生的認知規律，創設合適的真實情境，設計有意義的問題，促進學生對情境中的問題進行探究與思考。同時，“測量”試題的編制還要注重開放性，避免死記硬背的問題，在學生解題的過程中培養他們的創新意識。

（三）加強逆向思維考查，體現發展性

逆向思維是小學高年級學生在數學學習過程中逐漸形成的數學素養，也是學生學習數學知識所必須具備的能力［8］。逆向思維不僅可以幫助學生破除定向思維，培養多元思維習慣，還有助于學生提高創新意識，多角度解決數學問題。因此，“測量”試題的編制應該從多角度考查學生的測量素養和能力。同時，“測量”試題的編制還應創新解題模式，除了傳統的填空題、計算題、應用問題，還可以借助信息技術，采用拖拽、連線、實踐操作等形式考查學生的測量素養。

（四）優化表征方式，體現過程性

豐富的信息載體和多元化的表征方式有利于改善學生的作答感受，增添試題的趣味性，激發學生的思考能力，評價學生的實際水平。借助不同的表征方式，可以使試題更加靈活，從而增強試題的深度和廣度。采用多元表征的形式呈現試題時，試題的文字表達要簡潔，避免不必要的表達語句，且圖表和故事背景需符合學生的認知水平和生活經驗，以體現數學的文化價值。因此，未來我國編制“測量”試題要重視試題的表征方式，有效發揮試題的測評作用。

參考文獻：

［1］許添舒，臧悅，孔企平.小學數學“測量”課程國際改革動向分析［J］.小學數學教師，2018（4）：76-78.

［2］中華人民共和國教育部.義務教育數學課程標準（2022年版）［M］.北京：北京師范大學出版社，2022.

［3］王利慶.一道幾何參賽試題的編制、品析及感悟［J］.中學數學雜志，2021（6）：48-50.

［4］阿斯亞·圖爾蓀，王利，楊新榮.NAEP2019小學數學評估框架及試題特點分析［J］.小學數學教育，2022（21）：4-6.

［5］沈陽，張晉宇，鮑建生.表征在數學教育中的研究現狀［J］.數學教育學報，2022，31（2）：82-89.

［6］丁夢佳. 中美韓小學數學教材“測量”內容比較研究：以人教版、加州版、科創版為例［D］.青島：青島大學，2020.

［7］何學冬. 中新兩國小學數學“測量”內容的比較研究［D］.重慶：西南大學，2020.

［8］劉紅紅.逆向思維在小學高年級數學解題中的應用策略［J］.智力，2021（19）：77-78.

（江西科技師范大學數學與計算機科學學院）