怎么做能幫助學生更好地理解假分數

王蝶鳳

假分數是分數教學中的一個難點。為了幫助學生更好地理解假分數的含義，可以采用以下教學過程。

一、回顧舊知，引入分數度量的意義

1.教師用課件出示兩條線段（如圖1），并提問：如果線段①的長度是1米，那么你估計線段②的長度是多少？

2.教師用課件動態演示用線段②去測量線段①的過程（如圖2），得出線段②的長度正好是線段①長度的[13]，也就是1米的[13]，所以線段②的長度是[13]米。

二、探究新知，經歷假分數的產生

1.估一估。教師在圖1下方出示線段③（如圖3），請學生估一估線段③的長度。學生發現線段③比線段①長，長度大于1米，但具體長度需要測量。

2.量一量。學生會想到用[13]米去測量，可以讓他們在學習單上畫一畫，呈現測量過程。教師用課件動態演示測量過程（如圖4），發現正好有4個[13]米，也就是說，線段③的長度是[43]米。

3.議一議。引導學生思考：[43]米是如何產生的？它到底有多長？交流討論后反饋：[43]米就是把1米平均分成3份，1份是[13]米，4份的長度就是[43]米，也就是比1米還多了[13]米。

三、觀察比較，突破“假”在哪里

1.做一做。教師出示另外三條線段，引導學生用剛學的方法量一量它們的長度。學生量出三條線段的長度分別為[63]米、[73]米和[93]米。

2.比一比。學生觀察、比較各個分數，概括假分數的含義：分子比分母大或分子和分母相等的分數叫作假分數。教師提問：假分數是分數嗎？引導學生得出：假分數是大于1或等于1的分數。

3.想一想。教師提問：假分數與整數、真分數之間有什么關系？引導學生發現：[63]就是2，[93]就是3，[73]可以看作由[63]和[13]相加形成的數。由此可以看出：有些假分數的分子恰好是分母的倍數，它們實際上是整數；有些假分數的分子不是分母的倍數，這樣的假分數可以寫成帶分數。

四、多元表征，完善假分數的意義

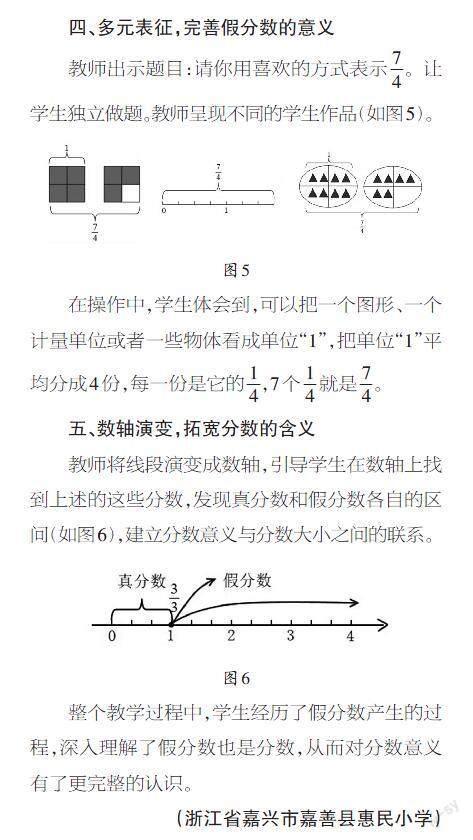
教師出示題目：請你用喜歡的方式表示[74]。讓學生獨立做題。教師呈現不同的學生作品（如圖5）。

在操作中，學生體會到，可以把一個圖形、一個計量單位或者一些物體看成單位“1”，把單位“1”平均分成4份，每一份是它的[14]，7個[14]就是[74]。

五、數軸演變，拓寬分數的含義

教師將線段演變成數軸，引導學生在數軸上找到上述的這些分數，發現真分數和假分數各自的區間（如圖6），建立分數意義與分數大小之間的聯系。

整個教學過程中，學生經歷了假分數產生的過程，深入理解了假分數也是分數，從而對分數意義有了更完整的認識。

（浙江省嘉興市嘉善縣惠民小學）