小學數(shù)學教學中正解植樹問題 教學誤區(qū)分析

陳文

摘 要：“植樹問題”是人教版五年級上冊“數(shù)學廣角”的內(nèi)容，筆者教學“植樹問題”后，發(fā)現(xiàn)學生在解答該內(nèi)容時速度較慢且錯誤多，與同年級組教師交流時發(fā)現(xiàn)也存在類似問題。教師教學的困惑在哪里？學生的問題有哪些？如何進行高效教學呢？筆者帶著這樣的疑問和自身對于課標、教參的一些理解，談一談自己在實踐中的思考。具體來說，從認識誤區(qū)、策略誤區(qū)、教法誤區(qū)三方面進行教學誤區(qū)分析。

關鍵詞：數(shù)學教學;植樹問題;教學誤區(qū)

一、認知誤區(qū)——“負面遷移”導致認知錯誤

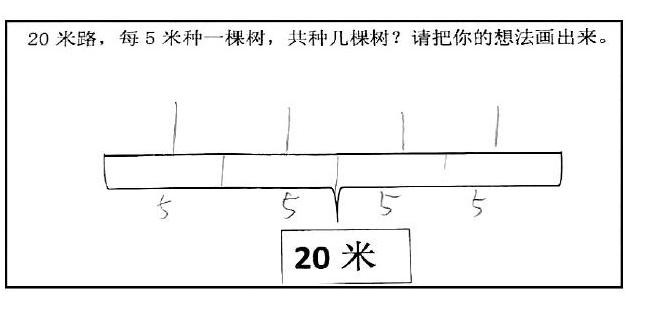
筆者抽取了作業(yè)本中較為典型的三道題目對本校學生進行了“植樹問題”的學習后測，測試題目和結(jié)果如下圖。

為何錯誤率居高不下呢？訪談后獲知，植樹問題的第一課時是學習兩端都種的情況，很多學生形成這樣的誤區(qū)：植樹問題肯定要先分段，分段后把樹植在段上，也就是段數(shù)和棵數(shù)是相等的。這樣的數(shù)據(jù)對于“只種一端”是相吻合的，但會對其他兩種情形的學習產(chǎn)生負遷移。

二、策略誤區(qū)——“低效畫圖”導致對應不清

本課教學設計思路多種多樣，但都有一個共同點，那就是“畫圖”。那么教師是如何教學生畫圖的呢？筆者截取了教參中的一段教學過程，如下圖。

教師先采用“化大為小”，使數(shù)據(jù)簡單化，后讓學生自主畫圖探究，在學生的畫圖過程中出現(xiàn)的形式很多，大致可以分為以下幾類。

教師針對出現(xiàn)的情況進行講解，得出棵數(shù)與間隔數(shù)，從而總結(jié)：兩端都種的棵數(shù)=間隔數(shù)+1。

看似數(shù)形結(jié)合非常緊密，實則學生并沒有充分理解棵數(shù)與間隔數(shù)之間的關系，更加不能理解點與段之間的一一對應關系，可以說是灌輸式教學。所以筆者把這種畫圖歸結(jié)為“低效畫圖”。

三、教法誤區(qū)——“萬能公式”導致囫圇吞棗

（一）學生層面——只知其然，不知其所以然

我們選取了本校五年級兩個班的78位學生進行了前測，整理后當即對其中的25位學生進行了追蹤式訪談，結(jié)果如下圖。

其中五（3）班的許同學的回答很有代表性。

師：（指著種一邊的+1）這里為什么要加1？你是怎么想的？

生：我以前在一個奧數(shù)班學過，老師說要先求出有幾段，然后加就好了。

師：老師有具體講為什么要加嗎？

生：記不起來了。

同日，我們對本校六年級已經(jīng)學過該知識一年的兩個班82位學生進行了后測，整理后當即對其中的25位學生進行了追蹤式訪談，結(jié)果如下圖。

對其中一位正確的學生——六（3）班楊同學進行的訪談如下。

師：剛才我們做了一道關于植樹問題的題目，你能說一說你的理解嗎？

生：上課時老師說過任何的植物問題我們都可以通過公式求得。

師：那你是怎么求的呢？

生：老師說過，我們要先求得間隔數(shù)，然后看到底是哪種情況，兩端都種的話棵樹等于間隔數(shù)加1，只種一端棵樹等于間隔數(shù)，兩端都不種棵樹等于間隔數(shù)減1。這道題目是兩端都種，所以我只要先求出有40個間隔，然后加1就可以了。

由此可知，在教學中，學生能熟記公式并正確判斷是植樹問題三種類型中的哪一種。但對于什么相當于“點”、什么相當于“段”混淆不清，在應用公式過程中錯誤頻出。

（二）教師層面——只教其然，簡教其所以然

“植樹問題”安排在“數(shù)學廣角”中，其用意是發(fā)展學生的合情推理和演繹推理。在實際的教學中，一部分教師的做法是直接告知學生只要看清題意中的“兩端都種”=間隔數(shù)+1、“只種一端”=間隔數(shù)、“兩端都不種”=間隔數(shù)-1，如果要求兩邊棵數(shù)，那就再乘2。

另一部分年輕教師接受的是新教學思想，緊跟時代潮流，先讓學生自主探索，然后全班交流。結(jié)果教師發(fā)現(xiàn)，在課堂反饋交流中往往被卷入學生“觀點紛爭”的漩渦中，教學費時間，學生抓不住植樹問題的本質(zhì)，最后教師只好“亡羊補牢”，但學生還是沒有真正掌握植樹問題的內(nèi)涵。下圖是筆者對本校王老師和李老師訪談的內(nèi)容。

顯然，對于第一種公式記憶和第二種“穿新鞋走老路”的教學方式，在一定的題目中出現(xiàn)了高正確率的假象，對于一些變式題及生活實際問題的解題，正確率呈跳崖式降低。

■參考文獻

[1]中華人民共和國教育部.義務教育數(shù)學課程標準（2011年版）[M].北京：北京師范大學出版社，2012.

[2]章宏俊.從“段數(shù)”入手探究植樹問題[J].教學月刊小學版（數(shù)學），2013（Z1）.

[3]程月明.植樹問題教材解讀[J].數(shù)學學習與研究，2013（18）.