讓圖形來“說話”

丁群俐　蔡水華

摘? ?要：

幾何直觀是《數學課程標準》提出的十大核心概念之一，本文從尋找直觀模型、注重自主操作、加強數形結合等教學策略出發，幫助學生直觀地理解數學問題的本質，讓幾何形體在學生頭腦中從“簡約”走向“豐盈”，以求更有效地培養學生的空間觀念和幾何直觀能力。

[關鍵詞 ] 幾何直觀;數學圖形;數學教學

著名數學家華羅庚說：“形缺數時難入微，數缺形時少直觀。”幾何直觀是揭示現代數學本質的有力工具。培養幾何直觀能力的策略有很多，本文從幾何直觀教學策略的角度出發，幫助學生直觀地理解數學問題的本質，有效地培養學生的空間觀念和幾何直觀能力。

一、尋找直觀模型，發展學生的直觀洞察力

1.以圖表思，形象直觀。《數學課程標準》指出：幾何直觀主要是利用圖形描述來分析問題。通過圖形將關鍵信息傳達出來，能幫助我們有效地思考問題、分析問題，尋求解決問題的方案。因此教師要善于借助幾何直觀，畫一畫、涂一涂，以圖導思，讓解題思路一目了然。

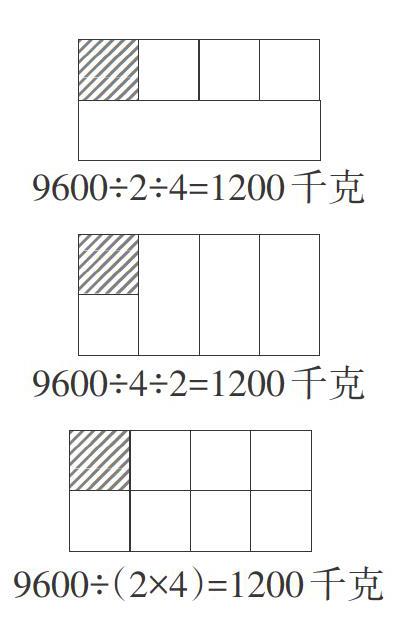
有這樣一道題：有一堆貨物共9600千克，需要2輛車分4次運完，那么每輛車每次運多少千克？

在解決問題前，教師提出要求：先列算式，然后在長方形圖中畫出解題思路。

反饋時，學生的回答很精彩：

學生通過分長方形來表示算式每一步表達的含義，清晰地描述了解題思路。教師較好地利用長方形溝通了解決問題、計算教學與空間圖形三者之間的關系，充分利用外化的“形”把內在的數學本質形象地表示了出來。

2.以圖促思，表征直觀。幾何直觀不僅應用于“圖形與幾何”的教學，在其他領域也發揮了不可替代的作用，而且貫穿于整個數學學習的過程中。它憑借圖形的直觀性特點將抽象的數學語言與直觀的圖形語言有機地結合起來，深入數學問題的本質，打開學生思維的大門，幫助學生理解數學知識的難點。

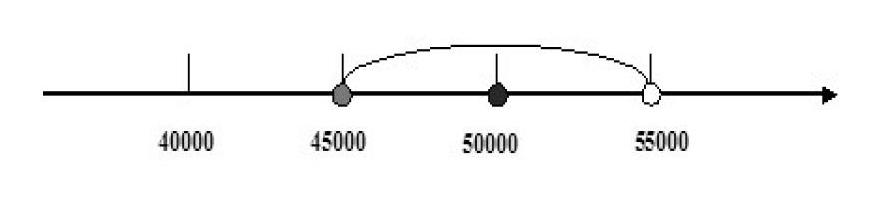
一個數的近似數是相對抽象的一個概念性知識，在作業中有這樣一道題：甲、乙兩個數，將甲數四舍五入省略萬后面的尾數約是5萬，將乙數改寫成以“萬”為單位的數是5萬，那么甲數和乙數的大小關系是（）。

A.甲數=乙數B.甲數>乙數

C.甲數<乙數D.無法確定

在解答這道題時，不少學生是舉例說明的，列出了兩個不同的數來比較，而有一個學生用數軸來表示，這樣就把其他同學說的情況都包括進去了。

從這道題的分析中，我們可以發現，數軸這種特定的幾何圖形在數與代數領域淋漓盡致地發揮了幾何直觀的作用，之前幾個同學說的都是零散的數，而這個同學利用數軸一下子把大家的思維聚焦起來，將這些數與數軸上的點一一對應起來，學生的思路也開闊了，而且這樣比較更方便、更直觀。

二、注重自主操作，發展學生的空間想象能力

1.借助自主操作，積累表象經驗。要培養學生的幾何直觀能力，不能光是教師畫，而要讓學生積極參與，自主操作。讓學生經歷用圖形來描述問題和分析問題，以達到解決問題的目的。

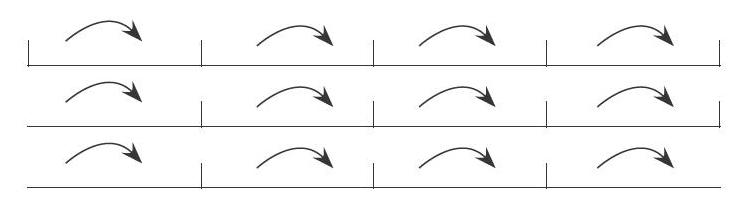
在教學“植樹問題”時，有位教師一開始就提出了一個比較開放的問題：在學校門口一條長20米的馬路一邊，每隔5米種一棵樹，能種幾棵樹？

當學生得出不同答案時，教師沒有馬上下結論，而是讓學生畫圖驗證自己的猜想：

根據這三幅圖，學生發現：當兩端都種時，棵數=間隔數+1;只種一端時，棵數=間隔數;兩端都不種時，棵數=間隔數-1。

植樹問題是比較抽象的問題，學生理解起來比較困難。學生通過直觀圖找到了各數量之間的關系，找到了解決問題的方法。通過畫線段圖，增強了學生對植樹問題的感性認識，有效地幫助學生理解了間隔數與棵數之間的復雜關系，積累了數學活動的經驗。

2.借助圖形，發展空間聯想。隨著年齡的增長，學生從生活中獲得了不少經驗，形成了一定的空間知覺和空間表象。在教學中教師可以借助直觀圖形，引導學生進行合理猜想，充分發揮學生的空間想象能力。

在學習“分數的認識”時，有一道這樣的題目：圖1中陰影部分可用[13]表示嗎？

學生看到這個圖馬上會判斷是錯的，因為它沒有平均分。

師：那這三份都不可能是[13]嗎？

師：中間那份真的是整體的[13]嗎？你們有什么好方法驗證一下？

學生邊觀察圖形，邊拿起筆思考。

在交流中，學生中出現了兩種思路，他們結合畫的草圖將想法清晰地表達出來。

在教學分數的意義時，我們發現，如果在課堂上大量使用“平均分”的分割線，在幫助學生形成分數概念的同時也對分數概念本質的理解起到了干擾作用。學生會認為只有分割成大小形狀一樣的圖形才能被稱為“平均分”。在這個教學片段中教師引導學生根據三角形圖形進行探索、觀察、操作、驗證，使學生對分數概念的本質有了更深刻的理解，思維也得到了很大程度的提升。

三、加強數形結合，提高學生的解決問題能力

1.以形助數，內化解題思路。在解決問題時，經常會發現學生找不到思路，或者列出了算式卻說不清楚解題方法，這時我們可以借助形象化的直觀圖形來幫助學生提取信息，找到解決問題的方法。

例如，一個底面是正方形的長方體，把它的側面展開后得到一個邊長是12厘米的正方形，求這個長方體的體積是多少？

初看這題似乎缺少條件，教師讓學生先根據信息畫圖（如圖2），將已知條件表示出來。

當學生畫出展開圖后，發現長方體的高就是12厘米，長和寬都是12÷4=3厘米，這個隱含的信息找到后自然就能求出長方體的體積。

在圖形與幾何的學習中，我們常常會碰到諸如此類的問題，學生往往不能直接找到相關的數據解決問題，這時畫圖就是一種很好的解題策略，可以幫助學生理清思路，找到隱含信息，從而解決問題。本案例中的圖形語言為數學思維活動提供了直觀模型，從而達到以形想數、化難為易、化隱為顯的目的。

2.數形互譯，外顯數量關系。數量關系是在具體情境中抽象概括出來的，具有高度的抽象性。教師可以借助幾何直觀的方法幫助學生理解和詮釋數量關系，化抽象為直觀，化內在為外顯，為學生在分析數量關系與解決問題之間搭起一座橋梁。

有這樣一道應用題：一塊長方形菜地，長與寬的比是7∶3，如果長減少12米，寬增加16米，就變成了一個正方形。這塊菜地的面積是多少？

學生解答這道題時感覺無從下手，教師引導學生畫出如下的線段圖（如圖3）：

學生借助線段圖更直觀地理解了“長比寬多出來的4份，就是16+12=28米”的結論。此時數量關系很明確，問題也就迎刃而解了。

內在的解題思路形象地外顯了，這樣的圖形直觀明了，易于理解，數形互譯，有效地凸顯了數形結合思想。

幾何直觀可以幫助學生直觀地理解數學問題的本質，在表征直觀、讀懂直觀中可以進行推理和想象，實現思維的頓悟。當然，幾何直觀能力的培養并不是一朝一夕的事，在教學中我們要根據學生的認知規律，采用合理的教學方式，促使學生對幾何形體有深刻的認識，使幾何形體在頭腦中從“簡約”走向“豐盈”，有效地培養學生的空間觀念和幾何直觀能力。