試論數(shù)形結(jié)合方法在高中數(shù)學教學中的應用

時蕾

【摘要】高中數(shù)學教學中影響教學質(zhì)量的因素比較多，如教學方法即為比較關(guān)鍵的影響因素.教師應將新型教學方法引入課堂中，這樣才能使學生的數(shù)學學習效率得到提升.高中數(shù)學知識抽象性強，教師需要借助數(shù)形結(jié)合的方法，幫助學生理解抽象性數(shù)學知識.文章就數(shù)學教學中數(shù)形結(jié)合方法的應用價值及影響因素進行闡述，然后就教學中應用數(shù)形結(jié)合的具體方法進行詳細探究，希望借此對學生高效學習數(shù)學知識起到促進作用.

【關(guān)鍵詞】數(shù)學教學；數(shù)形結(jié)合；方法應用

教師在為學生講解數(shù)學知識時，應該注重學生學習能力的培養(yǎng)，采用多樣化的方式開展教學，尤其要重視學生的主體地位，將學生的主人翁意識發(fā)揮出來，充分提高學生的學習能力.在教學抽象性較強的知識點時，教師要結(jié)合數(shù)形結(jié)合方法，引導學生從形的角度來理解抽象的數(shù)學問題，幫助學生提高數(shù)學學習能力.

一、在數(shù)學教學中應用數(shù)形結(jié)合方法的價值及存在的問題

（一）在數(shù)學教學中應用數(shù)形結(jié)合方法的價值

在數(shù)學知識教學中，教師要注重對抽象理論知識的講解.當學生的學習積極性不高時，教師應結(jié)合學生學習需要，對課堂教學方式進行創(chuàng)新，可將數(shù)形結(jié)合和數(shù)學教學相結(jié)合，為學生學習進步打下堅實基礎(chǔ).

1.助力學生解決數(shù)學難題

在數(shù)學學習過程中，學生解決問題能力的培養(yǎng)十分重要，直接影響到學生的綜合素質(zhì)提升.數(shù)形結(jié)合的方法為學生學習數(shù)學知識提供新的思考方式，有助于數(shù)學教學活動的高效開展.學生學習數(shù)學知識的過程就是學習解決問題方法的過程，由于數(shù)學課堂中的題目以及題型比較多，涉及的解題方法和思路也較為多樣，教師應用數(shù)形結(jié)合方法進行教學，有助于幫助學生找到問題突破口.只有在實踐教學中采用數(shù)形結(jié)合方式，讓學生將數(shù)和形進行結(jié)合，才能提高學生解決問題的能力.

2.有助于創(chuàng)新教學模式

對于數(shù)學教學來說，教師采用的教學方法直接影響到教學質(zhì)量，創(chuàng)新教學模式是提高數(shù)學課堂教學質(zhì)量的重要條件.在以往的灌輸式教學中，學生很難理解所學知識，尤其是數(shù)學基礎(chǔ)較差的學生，其學習效率比較低.數(shù)形結(jié)合為教師創(chuàng)新教學模式提供了方向，為高層次教學活動的開展打下了堅實基礎(chǔ).結(jié)合數(shù)形結(jié)合進行教學是符合新課改要求的，也是對傳統(tǒng)數(shù)學課堂教學的優(yōu)化創(chuàng)新，可以讓學生直觀地理解抽象數(shù)學知識，拓寬學生視野.

3.促進學生搭建系統(tǒng)知識框架

采用數(shù)形結(jié)合的方法有助于學生搭建系統(tǒng)性知識框架.高中數(shù)學教師要向?qū)W生強調(diào)掌握解題方法的重要性，在解題過程中培養(yǎng)學生的邏輯思維和解題能力.數(shù)學知識一般由數(shù)字、字母與公式組成，教師需要發(fā)揮數(shù)形結(jié)合的作用，讓學生在數(shù)學知識學習中搭建系統(tǒng)的框架，由此使得學生數(shù)學學習效率得到提升.

（二）限制數(shù)形結(jié)合應用效果的因素

1.教師因素

教師自身的教學理念及經(jīng)驗方法是自成一體的，每位教師的教學理念及經(jīng)驗方法都有不同之處，部分教師對數(shù)的運算比較精通，而部分教師則更擅長解釋數(shù)量關(guān)系.教師自身參與培訓，汲取、更新自身專業(yè)知識，創(chuàng)新教學方法以及教學思想，將數(shù)形結(jié)合融入教學，有助于提高數(shù)學教學質(zhì)量.另外，教師自身思維能力以及對教材知識的掌握程度，也會影響學生數(shù)學知識學習質(zhì)量的高低，教師采用的教學方式，以及圖形繪制的能力，對學生理解抽象的數(shù)學知識都有著較大影響，所以，在數(shù)學課堂教學中，教師在應用數(shù)形結(jié)合方法時，要提高自身教學能力，才能更好地為學生學習數(shù)學知識提供服務.

2.學生因素

高中生在數(shù)學知識的學習中，如果沒有真正地理解與掌握數(shù)學知識，且思維邏輯能力、思考能力較差，就會影響數(shù)形結(jié)合方法的應用質(zhì)量及效果.學生自身對數(shù)形結(jié)合的認識理解程度，以及思維邏輯轉(zhuǎn)化和思考問題能力水平等，都會對數(shù)學知識學習質(zhì)量、效果產(chǎn)生很大的影響.

二、在數(shù)學教學中應用數(shù)形結(jié)合方法的實踐措施

為了提高數(shù)學教學中數(shù)形結(jié)合方法的應用質(zhì)量，教師要準確把握數(shù)形結(jié)合方法的應用價值，從多角度進行考量，充分發(fā)揮數(shù)形結(jié)合方法的優(yōu)勢.

（一）數(shù)形結(jié)合把握數(shù)量關(guān)系

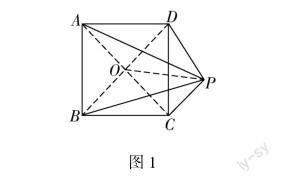
高中數(shù)學知識都比較抽象，教師在數(shù)學教學中，應該將學生的主體地位充分發(fā)揮出來.學生愿意積極主動地學習數(shù)學知識，才能取得理想效果.同時，教師還要采用數(shù)形結(jié)合的方式讓學生準確把握數(shù)量關(guān)系.把圖形信息轉(zhuǎn)變成代數(shù)信息，能幫助學生將重點放在數(shù)量關(guān)系討論上，通過代數(shù)運算并借助代數(shù)的精確性解決實際問題.另外，教師還可通過坐標法來幫助學生解決數(shù)學問題.所謂的坐標法就是解析法，也就是在教學過程中通過把平面圖形放在直角坐標系當中，讓點與坐標一一對應，能方便學生明確角的度數(shù)以及線段長度之間的數(shù)量關(guān)系.學生在解決數(shù)學問題的時候，如果缺乏解題思路，就要注重發(fā)揮坐標法的作用.同時，利用向量處理幾何問題，能夠給學生帶來高效的學習效果，消除傳統(tǒng)解法的局限性，簡化證明過程.如矩形所在平面內(nèi)任一點與矩形對角線端點構(gòu)成的兩條線段平方和相等，如圖1，點P是矩形ABCD所在平面內(nèi)任意點，有PA2+PC2=PB2+PD2，如果通過傳統(tǒng)幾何證明方式證明該式，涉及的思維量比較大，技巧性強，如果通過解析法的方式計算，過程也比較復雜.此時，如果利用向量的方法，通過數(shù)形結(jié)合的方式就能幫助學生把握數(shù)量關(guān)系，簡化推理過程.

（二）數(shù)形結(jié)合緊密聯(lián)系教材文本

講述數(shù)學知識中，教師要靈活運用數(shù)形結(jié)合的方法，結(jié)合學生素質(zhì)培養(yǎng)的需要，將數(shù)學教材中的文本內(nèi)容和數(shù)形結(jié)合相結(jié)合，讓學生明確不同知識點之間的邏輯關(guān)系.把數(shù)形結(jié)合方法和教材內(nèi)容相結(jié)合，能夠體現(xiàn)出新課改的本質(zhì).教師可通過把復雜抽象的數(shù)學知識轉(zhuǎn)變成生動形象的圖形，引導學生自主分析、觀察，調(diào)動學生學習探究的動力，強化學生視覺感官體驗.例如，數(shù)學教師在為學生講授不等式知識點的時候，若改變以傳統(tǒng)方法教授絕對值不等式求解技巧的現(xiàn)狀，通過數(shù)形結(jié)合的方式讓學生進行對比、處理和分析，則可加強學生對絕對值幾何意義的認識.以學生為中心的教學形式，符合課程改革要求，能讓學生在學習中自主判斷，分析不同解決問題的方法，從宏觀角度認識數(shù)形結(jié)合思想方法的優(yōu)勢，并在后期的自我教育中促進學生學習成長.

（三）數(shù)形結(jié)合促進學生形象思維發(fā)展

（四）數(shù)形結(jié)合提高學生學習興趣

學生的數(shù)學知識學習效率在一定程度上與興趣有著密切聯(lián)系，學生只有對數(shù)學學科感興趣，才會全身心地投入數(shù)學學習中.學生學習數(shù)學知識的動力源于興趣的激發(fā).教師要對學生的學習情況及興趣進行了解，在學情分析之后為學生設計數(shù)形結(jié)合的題目，使學生轉(zhuǎn)變以往被動的學習狀態(tài)，積極參與數(shù)學課堂，才能對學生學習進步起到促進作用.數(shù)形結(jié)合的方式能讓學生感受到數(shù)學學習并非枯燥乏味，而是十分有趣的.學生在數(shù)形結(jié)合的學習方法支持下進行探究，其學習的動力能被充分調(diào)動起來，綜合能力也能得到提高.如集合知識點涉及的抽象內(nèi)容比較豐富，有交集、補集和并集等，教師如果單一地為學生講述概念，學生在理解的時候就會存在難點.教師可將數(shù)和形進行轉(zhuǎn)化，通過為學生設計直觀的圖形，讓學生明確集合當中的數(shù)據(jù)及關(guān)系，同時將抽象的數(shù)學知識以生動形象的方式展示出來，使學生對數(shù)學學習的積極性得到大大提升，方便學生掌握數(shù)學知識.教師可利用Venn圖把涉及的元素放入正確位置，進而得到所求的集合.

（五）數(shù)形結(jié)合優(yōu)化數(shù)學作業(yè)設計

要想使學生的數(shù)學學習效率得到提升，教師要在不同的教學環(huán)節(jié)充分發(fā)揮數(shù)形結(jié)合方法的作用，使得學生在實踐學習中，不斷提升自主學習能力、探究能力.教師要針對學生數(shù)形結(jié)合思維能力培養(yǎng)的需要，科學設計作業(yè)內(nèi)容，通過引導學生參與數(shù)學作業(yè)實踐，使學生的數(shù)形結(jié)合意識得以形成，幫助學生掌握解題方法與技巧，提升學生解題能力.針對作業(yè)設計，教師不僅要結(jié)合教材內(nèi)容，還要與學生的實際情況結(jié)合起來，這樣才能讓學生更積極地參與數(shù)學教學活動，應用數(shù)形結(jié)合思想解決數(shù)學作業(yè)中的問題，提高學生解決問題的能力.

例如，教師在為學生講完“函數(shù)”內(nèi)容后，為幫助學生樹立數(shù)形結(jié)合意識，就要從數(shù)形結(jié)合的角度設計數(shù)學作業(yè)，引導學生在作業(yè)中運用數(shù)形結(jié)合的方法解決問題，增強學生的數(shù)形結(jié)合意識.函數(shù)知識抽象性比較強，學生很難理解，所以教師在為學生設計作業(yè)的時候，就要通過數(shù)形結(jié)合的方式，使學生直觀地思考抽象的函數(shù)問題，增強學生的理解能力，提高學生函數(shù)計算的準確度.如，教師可為學生設計這樣的作業(yè)內(nèi)容：“方程sin2x=sinx在區(qū)間（0，2π）上解的個數(shù)是（ ）.”這是典型的數(shù)形結(jié)合例題，學生在解題的時候要通過數(shù)形結(jié)合的方式，畫圖解題，如圖3所示.

（六）數(shù)形結(jié)合強化學生的數(shù)學運算能力

在數(shù)學課堂教學中，教師在對具體知識點進行講解時，要凸顯出學生學習探究的主體性，增強學生學習的主觀探究意識.高中生的學習思維已經(jīng)相對成熟，教師在數(shù)學課堂教學中，不僅要傳輸給學生理論性的知識，還要讓學生真正地掌握學習數(shù)學知識的方法，使學生能自主思考問題、解決問題，由此使其數(shù)學學習能力得到提升.高中階段的數(shù)學知識有著較大的學習難度，所以在實踐探究中，教師應該引導學生在解題時采用正確的方法，使學生的研究能力得到提升.數(shù)學教學中提高學生的運算能力是重要任務，教師在為學生講述具體數(shù)學運算知識點時，若將數(shù)形結(jié)合的思想融入其中，則能有效提高學生數(shù)學知識學習的質(zhì)量、效果，促進學生高效學習.教師在為學生講授“數(shù)學運算”知識點時，可通過數(shù)形結(jié)合思想的滲透，幫助學生了解數(shù)和圖之間的關(guān)系，讓學生產(chǎn)生直觀的感受，明白算理，這對提高學生的運算能力有著積極意義.

結(jié) 語

綜上，在數(shù)學課堂教學中，教師要將數(shù)形結(jié)合與具體數(shù)學知識內(nèi)容教學緊密結(jié)合起來，讓學生在數(shù)學課堂中發(fā)揮自身主人翁的角色，積極參與到數(shù)學課堂中，使其各方面的能力得到提升，包括探究能力、解決問題能力等.在數(shù)學教學中，教師應該注重培養(yǎng)學生的思維能力，還需要對數(shù)學課堂教學方法不斷創(chuàng)新，讓學生在掌握數(shù)學學習方法的基礎(chǔ)上，自主對數(shù)學知識深入探究，從而真正地理解與掌握所學知識，為構(gòu)建高效的高中數(shù)學教學課堂奠定基礎(chǔ).

【參考文獻】

[1]林榮元.探究數(shù)形結(jié)合思想在高中數(shù)學教學中的應用[J].新課程，2021（36）：125.

[2]盧燕春.數(shù)形結(jié)合思想方法在高中數(shù)學教學中的應用研究[J].考試周刊，2021（66）：82-84.

[3]李志琴.數(shù)形結(jié)合思想方法在高中數(shù)學教學與解題中的應用[J].新課程，2021（31）：128.

[4]趙文奎.高中數(shù)學教學時數(shù)形結(jié)合方法的應用[J].當代家庭教育，2021（21）：11-12.

[5]劉彩艷.數(shù)形結(jié)合教學方法在初中數(shù)學教學中的應用效果分析[J].數(shù)學學習與研究，2021（21）：30-31.

[6]盧思聰.高中數(shù)學教學中數(shù)形結(jié)合方法的有效應用[J].高考，2021（20）：24-25.

[7]屈玉華.探究數(shù)形結(jié)合思想在高中數(shù)學教學中的應用[J].讀寫算，2021（19）：105-106.