關注問題設計，精準實施教學

杭太宏

[摘? 要] 問題設計關乎課堂教學的成敗，在教學中要進行問題設計的研究，通過富有思考性的問題調動學生的積極性，催生精彩的智慧課堂.

[關鍵詞] 問題設計;教學策略;思維發展

課堂教學是通過問題進行貫穿和推進的，因此問題設計的質量直接決定了教學的效果. 好的問題設計不僅能緊扣教學目標，而且能引發學生思考，激發學生探究的好奇心. 在教學準備中除了準備教學內容和教學過程的設計之外，還要關注問題的設計，高質量的問題設計應是圍繞教學目標環環相扣，可以幫助學生構建起知識的完整體系，引發學生的深度思考，使課堂教學更加流暢自然，立意高遠.

當然在教學中因為問題設計的單一乏味或者脫離教學目標任性隨意，也會影響整節課的教學效果. 因此，關注問題設計，使課堂富有活力和智慧，增添靈動和生命力，促進學生學習興趣的保持就顯得尤為重要. 筆者以兩個教學片段為例，談一談課堂教學中如何進行有效的問題設計.

關于“平行四邊形”教學的問題設計

關于平行四邊形的教學，在傳統的教學中一般會通過圖片或者幾何畫板，讓學生感知四邊形的特征以及在現實生活中的應用價值. 長期以來，這樣的導入方式因其直接和便捷，被很多教師推崇. 但是細細品味，這樣的導入方式卻少了一些數學的味道和值得細細欣賞的韻味. 下面筆者將展示一段別樣的教學實錄：

（一）課堂實錄

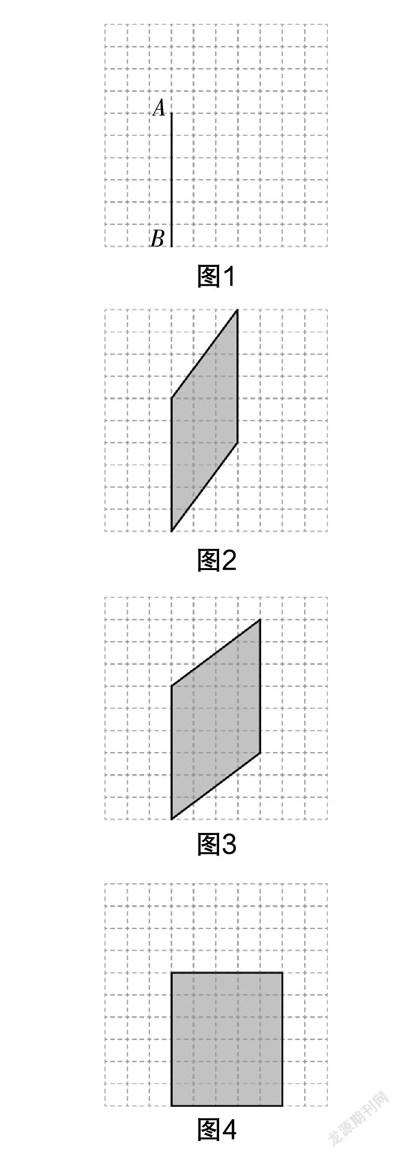
師：如圖1，請畫一個平行四邊形，要求以AB為一邊，鄰邊的和為11，頂點在格點上（小正方形的邊長為1）.

生：在紙上進行練習，畫出符合要求的平行四邊形.

師：同學們都非常厲害，已經找到了幾種答案，下面請幾位同學進行展示.

學生代表上臺進行展示，如圖2、圖3、圖4.

師：同學們已經可以畫出圖形了，那么誰能證明所畫的圖形就是滿足條件的平行四邊形呢？

生1：我們可以通過圖上的網格來得到三角形全等，從而知道兩組對邊分別平行.

師：那么這幾組平行四邊形有哪些區別和聯系呢？

生2：這幾個平行四邊形可以從邊長、周長、面積、內角等進行比較，通過網格可以看到它們的相同點和不同點.

師：如果我們放寬限制，不要求平行四邊形的頂點在格點上，那么可以畫多少個滿足要求的平行四邊形呢？

生3：可以畫無數個.

師：好的，那我們通過幾何畫板進行演示一下. （確實可以畫出無數個）我們有沒有思考一下，為什么在限定的條件下還可以畫出無數個平行四邊形呢？

生4：因為只要平行四邊形的邊長和周長不變，它的內角、面積和高都可以隨意變化，形狀會發生改變.

師：展示生活中的一些物體圖片，如可以升降的晾衣架、校園的伸縮門等. 這些物體都具有平行四邊形的形狀，那么如果這些物體不使用平行四邊形，還具有同樣的特質嗎？

生：（有的說應該有，有的說沒有）

師：用一個由四根木棍組成的四邊形進行演示，將四邊形進行拉伸和擠壓. 同學們觀察一下這個四邊形經過擠壓和拉伸之后，形狀是否發生了改變.

生：改變了.

師：這就是四邊形的不穩定性，正是因為這種特殊性，其在生活中有著廣泛的應用. 你們能列舉出生活中的一些使用例子嗎？

學生紛紛列舉實例，并進行討論.

（二）設計評析

觀察整個教學實錄，始終以問題為導向進行梳理和推進，學生在問題的引導下始終保持著探究的好奇心，積極思考討論，踴躍地動手實踐操作. 學生通過問題思考，自主發現了四邊形的規律，理解了其“變”與“不變”的本質，感受到四邊形的特質. 這些問題具有非常高的質量，使課堂充滿了活力，仔細研究發現這些問題具有如下的特征：

1. 具有思考性

問題設計具有思考性，體現在思維的寬度和深度. 首先題目的設計不是封閉的，具有開放性的特點，因為其開放性可以調動學生積極思考，主動學習，從而保持思維的活力. 其次，從思維的深度來說，它是有一定的難度的，不是知識的記憶或者再現，而是需要經過思考之后才能獲得的答案.

在上述案例中，組織學生進行作圖符合要求的平行四邊形和討論四邊形的相同和不同之處，就是兩個具有開放性的問題，這樣的問題既具有一定的挑戰性，可以激發學生的探究欲望，訓練學生的深度思維，又具有開放性，能給予學生充分的思考空間.

2. 具有合適的難度

難易適中是高質量問題的重要特點，具有一定難度的問題才有思考的價值，可以激活學生的思維. 如果問題過于簡單，不能起到鍛煉學生思維的作用，難以深入探求問題的本質;相反，如果難度太大，學生經過思考難以解決，則會挫傷學生學習的積極性. 因此在問題設計中應既符合學生的“最近發展區”，在學生已有的知識經驗的基礎上進行設問，又要通過新舊知識的聯系才能解決，即需要“跳一跳”才能“夠得著”，使學生的現有知識不斷躍升到新的層次，發展為更高水平的“最近發展區”.

如本例中要求學生根據已經學習的平行四邊形的定義進行作圖，就符合學生的“最近發展區”理論. 在此基礎上，教師又進一步追問，如何證明平行四邊形？這樣的設問在新舊知識之間架起了橋梁，提升了難度，達到了既鍛煉學生的思維又鞏固學生所學的效果，提升了學生的認識.

關于“認識函數”教學的問題

設計

（一） 課堂實錄

學生在學習了函數的知識之后，教師進行了如下的問題設計：

國內投寄信件應付郵資：

1. 提問：如果郵寄質量為5克的信件應付多少郵資？郵寄10克的呢？

生：第一個空格應該是0.80.

師：還會有其他的數值嗎？

生：不會.A770A41B-28F9-47F0-8DC2-DE44C06F6493

師：那么我們把表格的其他答案也填一下，當m的值為5時，y的值為0.80.

2. 討論：y是m的函數嗎？

生1：y不是m的函數，因為當郵寄5克和10克的信時，所付的郵資都為0.80元.

師：大家覺得他的說法對嗎？

生2：我覺得他的說法是錯誤的，因為雖然寄5克和10克的信時，所付的郵資都為0.80元，但是寄5克的信時，所付的郵資是唯一且固定的，寄10克的信時，所付的郵資也是唯一且固定的. 以此類推，對于m的每一個確定的值，y都有固定且唯一的值. 因此根據函數的概念，y是m的函數.

師：非常精彩，那么為什么第一位同學判斷錯了呢？

生3：因為他把判斷的標準搞錯了，他認為相同的y值對應不同的m值就不是唯一了.

師：是的，在判斷函數的定義時要抓住y值對應每一個m值是否唯一且確定. 如果把表格中的條件稍作變動，將40

生4：不是的，因為假如m的值為31，那么y就有1.60和2.40兩個值，就不是唯一的值了.

師：講得非常好，這是一種通過反例驗證的方法.

（二）設計評析

首先，在學生學習了函數問題之后，進行了“郵資問題”的檢測，看起來挑戰過大，其實卻有著特定的用意：第一是為了激活學生的思維，通過有一定難度的試題給學生造成一定的困難. 第二是關注不同層次的學生，學生在面對困難之后會積極地調動已有的知識，在不斷探索中逐漸深化認識. 從課堂的實踐看來，對于郵件數量與郵資之間的關系，學生產生了不同的認識，這種不同的觀點激發了學生思維的火花，使學生對于函數的概念逐漸清晰，并在討論中逐漸產生共同的觀點. 通過師生和生生互動，使課堂不斷生發出新的增長點，推向高潮.

其次，本案例中體現了對學生學習熱情的保護，教師創設了平等交流的氛圍，營造了良好的環境，給了學生充分的思考空間，使學生敢于質疑. 通過教師的引導學生能夠發現并提出問題，并在教師的鼓勵下敢于提出問題，促進了思維的發展.

第三，教師還注意追根究底，當學生已經回答出正確答案之后，教師仍然繼續追問，上一位學生的錯誤在哪里？這樣適時的追問，可以讓問題的本質逐漸呈現，也培養了學生敢于打破砂鍋問到底的精神.

總之，問題的生發是促進學生不斷提升自身能力的關鍵點，如何引導學生提問，是教師在教學中要思考和研究的問題. 通過教師的引導、創設，學生通過解決問題到再次發現和提出問題，能推動自身思維的發展和學習能力的不斷提高.A770A41B-28F9-47F0-8DC2-DE44C06F6493