基于數學核心素養的課堂教學轉型

葉建聰

[摘 ?要] 知識與文化、理論與應用、預設與生成、結果與過程、演繹與歸納、論證與實驗等教學矛盾無時無刻不在激化，也引發了無數多次的教育轉型. 在新課改的浪潮下教師要想迅速地轉變觀念，提高自身業務水平就要創設良好的學習情境，謀求與學生的共同發展. 教師的教學智慧在于對學生內在的激發，對課堂互動的思考，對學生探究的促進，等等. 所以回歸數學的本質，體現數學的思考方式：以典型、簡單的數學對象為載體，在數學知識的發生發展過程中，培養學生的理性思維，發展學生的數學學科核心素養.

[關鍵詞] 核心素養;教學改型;數學思維

數學核心素養是當代最時髦的一個名詞，它高于一般數學思維方法的抽象意識，讓人從數學的角度即理性、科學嚴謹、邏輯清晰地去分析解決問題. 數學核心素養包括：數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析等. 這些數學核心素養既有獨立性，又相互交融，形成一個有機整體. 教好數學就是落實數學學科核心素養，如何抽象數學對象、如何發現和提出數學問題作為教學的關鍵任務，以實現從“知其然”到“知其所以然”再到“何由以知其所以然”的跨越[1]. 教學有具體措施，要把數學學科核心素養落實在數學教育的各個環節.

當前的教學，主要問題是數學沒有講好，教師不知道如何“示以思維之道”. 本文以“定積分在幾何中的應用”為例，闡述如何進行高中課堂教學轉型.

知識與文化相結合

數學知識是數學文化的一部分，知識被文化所涵蓋，二者相輔相成. 在數學研究中，研究出一個結論，這是科學;為什么要研究，怎樣研究，價值何在等，這些就是數學文化. 關于數學文化，在知識引入的情境中加入文化元素，在知識產生的歷史過程中滲透文化元素，在知識蘊涵的思想方法中解析文化元素，在知識應用的社會環境中欣賞文化元素.

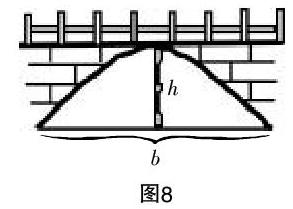
首先情境導入：講述古代數學家劉徽、祖暅、阿基米得等人的故事及微積分的發展史，接著展示一幅大橋油畫.

提出問題1：如何求出拱形的面積呢？

提出問題2：一拱橋的形狀為拋物線（如圖1所示），已知該拋物線拱形高為h，寬為b. 求證：拋物線拱形的面積S=bh.

帶著問題學生開始進入本節課的學習.

通過講述數學家的故事以及定積分的數學史，在數學史中去尋求答案. 數學發展與數學家的精神、態度相關，可彰顯科學家的精神. 留下懸念，激發學生的探索求知欲望，為后面探究性學習做好鋪墊. 同時對生活中的數學進行建模，培養學生數學建模素養，告訴學生定積分在社會、經濟建設應用的價值及數學美學的價值.

結果性知識與過程性知識相結合

指向核心素養發展的教學，不僅要把知識結果告訴學生，還要揭示知識發生、發展過程，而且把外延與擴展告訴學生. 過程比結果重要，二者相互整合，才能達到最佳的效果. 完整的教學應當是：知識從哪里來？知識是什么？知識往何而去？

筆者開始講授由曲線所圍平面圖形的面積：

筆者穿插定積分的概念、微積分基本定理、定積分的幾何意義復習，學生通過完成校本作業，自主建構所學定積分的知識儲備，有利于本節課的學習. 本環節安排學生談論，發現問題解決方向. 引導學生觀察圖形抽象出求面積的定積分，從直觀想象自然過渡到數學抽象，從面積差的求法則體現了轉化與化歸的數學思想.

學科性知識與實踐性知識相結合

指向核心素養發展的教學，就是要走出學科性知識教學的圍欄，將實踐性知識融入教學的過程之中，學科性知識與實踐性知識相互滲透、共同作用[2]. 自主性學習和探索性學習，師生將實踐性與學科性有效融合.

師：你能按照剛才討論的共識解答該題嗎？還有什么不明白的地方？

學生開始做題，得出答案.

師：通過第一道例題的學習，你有什么收獲嗎？求平面圖形的步驟是什么？

生：①作圖像（弄清相對位置關系）;②求交點的橫坐標，頂出積分上下限;③確定被積函數;④用定積分表示所求的平面曲線面積;⑤）計算定積分求面積.

師：還有什么要補充的？

生：解題、作圖注意規范……

通過追問引導學生對本題思考方向，在難點處追問，提供思考的臺階. 通過本題的解決，引導學生去探索、實踐，讓學生體驗思路的形成過程，學會分析問題的方法，初步梳理出在直角坐標系下求平面圖形面積的步驟. 安排學生自主性學習等實踐活動，鍛煉學生思維的獨創性.

外顯性知識與內隱性知識相結合

內隱性知識指不以文本形式顯性表述的，潛藏于顯性知識深層的隱性知識. 包括知識的文化元素、知識的過程元素、知識的邏輯元素、知識的背景元素等. 內隱素性知識是一種客觀存在的知識，它是被外顯知識所包裹的知識內核[3].

師：一道題有多種方法怎么辦？有沒什么啟發或注意點？

生：用最簡單的方法.

生：用我們最熟悉的類型：以x為積分變量.

師：有沒有什么注意點？

生：要將曲邊形轉化成我們諳熟的平面圖形，如三角形、平行四邊形、梯形或多種直邊形組合的圖形.

本例采用“一題多解”教學，有助于培養學生的發散思維，同時也進行優化方案. 采用教師追問，讓學生清晰思路，降低思考難度，又不減少思維量. 提高了學生的作圖能力，鍛煉了學生的想象能力. 體現了對稱的思想和分類思想，培養了學生的觀察能力和分析思考問題的嚴密性，培養了數學運算、數學抽象及邏輯推理素養.

證實性知識與證偽性知識相結合

教學應當是一種由知識的不確定性到知識確定性的漸進過程. 知識的不確定性階段是指提出問題和判斷問題，證偽在這一階段扮演著重要角色;知識的確定性階段是對知識的確認，證實在這一階段起著重要作用[4]. 把“數學對象的抽象——組成元素的提取——相互關系的猜想——猜想的證明——性質的應用”等落實下來. 能夠對數學問題進行變式、拓展和推廣，提出富有見解的數學猜想，并能證偽和證實猜想.

師生互動，介入開放性、探究性的問題.

師：為什么這樣做，是否合理？

師：還有沒有辦法呢？

解決一個數學問題時，用到的知識與方法可能是多樣的，比如說這題，它涉及拋物線、定積分、幾何等知識. 這便是知識遷移. 知識遷移是多種知識綜合，是跨情境的應用. 這就需要學生有豐富的知識資源，并能選擇有用的資源在新的情境中進行組合.

第斯多惠曾說過，“不好的教師奉送真理，好的教師教人發現真理”.教師應注重過程教學而不能僅僅傳授結論，學之道在于“悟”，教之道在于“度”. 總之，在新課改的浪潮下教師要想迅速轉變觀念，提高自身業務水平就是創設良好的學習情境，轉變教學思路，謀求與學生的共同發展.

參考文獻：

[1] ?劉明明. 勾股定理的探索與證明[J]. 中學數學教學參考，2019（01）.

[2][3][4] ?喻平. 發展學生學科核心素養的教學目標與策略[J]. 課程·教材·教法，2017（01）.