畫一畫，輕松學數學

沈秋紅

【摘? ?要】在數學教學中，應當注重培養學生的幾何直觀意識。尤其在一年級的教學中，幾何直觀是課程的基本要求，根據教學內容和一年級學生的認知發展規律，教師可采用畫圖解題的策略，逐漸提升學生的解題能力。

【關鍵詞】小學數學;幾何直觀;畫圖

幾何直觀主要是指利用圖形描述和分析問題。借助幾何直觀可以把復雜的數學問題變得簡明形象，有助于探索解決問題的思路，幫助學生直觀地理解數學問題，在數學學習過程中發揮著重要作用。《義務教育數學課程標準（2011年版）》中對培養學生的幾何直觀能力有四方面建議：一是在教學中使學生逐步養成畫圖習慣;二是重視變換，讓圖形動起來;三是學會從“數”與“形”兩個角度認識數學;四是掌握運用一些基本圖形解決問題。

在一年級的數學教學中，畫圖最有助于描述和分析問題。從一年級開始培養學生的幾何直觀能力，利用幾何直觀幫助學生理解數的概念和運算的道理，分析數量關系和解決實際問題，是非常有必要的，也是十分有益的。

一、畫圖解題，變抽象為直觀

一年級學生對數的認知尚處于起步階段，直接運用算式思考并解決問題的能力不足。用畫圖的方式把問題具體化，可以將抽象的數學問題形象化。如教學人教版一年級上冊第六單元《11～20各數的認識》中的例6。

要解決“小麗和小宇之間有幾人”這一問題，一年級的學生很難用算式來表示，出現了不同的錯式：10+15=25;15-10=5;15-10+1=6……究其原因，學生對題意不理解，不明白“之間”兩字的含義，更重要的是，學生解決問題的經驗不足，沒有好的方法。教師教學時可指導學生用畫圖的方法予以解決。

（一）注重讀圖訓練，捕捉信息

教學應該為學生創造經歷解決問題全過程的機會，注重培養學生從圖中捕捉信息、提出問題的意識和能力。

（二）指導畫圖，變抽象為直觀

喜歡畫圖是孩子的天性，教師可引導學生用畫圖的方法，數一數小麗和小宇之間的人數。

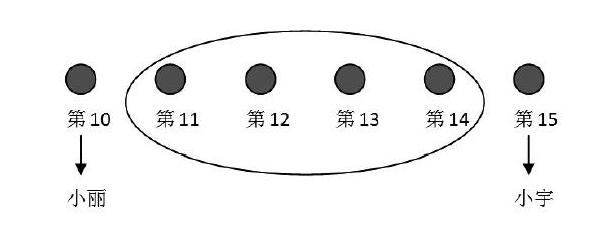
從上面畫的圖中，學生一眼就看出，小麗和小宇之間有4人。

生：以后要我們解決這樣的問題，我只要畫一畫圖，答案就出來了。

生：從圖上我還能知道小麗前面有9個人。

生：我明白了我寫的算式（15-10=5）錯在哪里了，我沒有把排在第15的小宇去掉，所以15減10再減1就對了，答案就是4人。

……

師：看來，簡簡單單一幅圖，能幫助我們找到問題的答案。

（三）舉一反三，練習應用

教師出示問題組：

①有一排兔子，從左往右數，小灰兔排在第5，從右往左數，它排在第4，一共有幾只兔子？

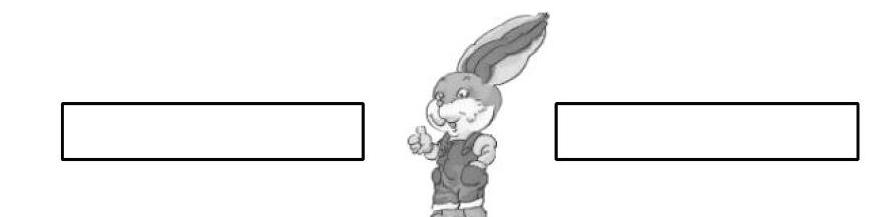
②有一排兔子，小灰兔的前面有5只，后面有4只，一共有幾只兔子？

這兩個問題，學生很容易混淆，弄不清楚什么時候要加1，什么時候不用加1，什么時候要減1。教學時，引導學生把題目的意思轉化成圖形的形式，學生就不難得到解答。

通過對這組問題的畫圖解答，還可以使學生對基數和序數含義的認識直觀化。

從開始學習數學起就養成畫圖的習慣，能使學生真正體會到畫圖對理解題意、尋求解題思路帶來的益處。在教學中應該有這樣的導向：能畫圖時盡量畫;把問題、計算等數學內容變得直觀了，就容易展開形象思維。

二、適時提升，豐富畫圖策略

不同的學生畫圖時會有不同的思路。學生畫圖應經歷從直觀到抽象的提升過程，體會在不改變數學信息和數量關系的前提下可以畫不同的圖，并使圖變得簡潔、抽象。如在學習“比一個數多（少）幾的問題”新課時，學生可經歷以下畫圖過程。

（一）用好直觀圖，拓展學生對減的意義的理解

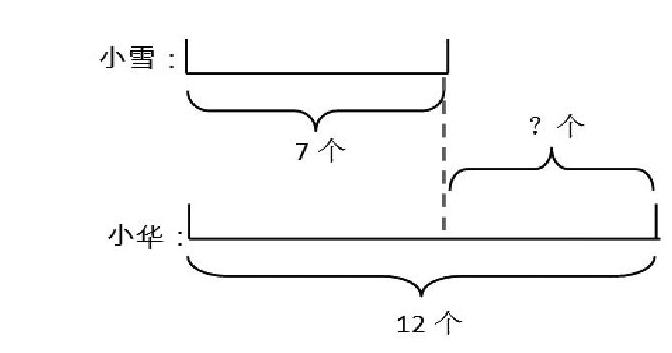
如“小雪套中了7個，小華套中了12個。小華比小雪多套中幾個？”

師：誰和誰比？誰套中的多？

生：小華和小雪比，小華套中的多。

師：你能用○來表示他們套中的個數，畫一畫圖嗎？

小華比小雪多5個

（二）優化畫圖方式，進一步理解數量關系

生：老師，我覺得畫圓圈太麻煩了，要畫這么多個圓圈，如果個數再多一些的話就更麻煩了。

師：你有沒有更好的辦法呢？

生：畫線段圖。

雖然實物圖和線段圖都具有直觀性，但相對而言，線段圖無疑更抽象些。學生對物體數量的理解與表達僅依賴于數與物的對應表征是不現實的，從實物圖到線段圖的過程，符合低年級學生的認知發展規律，能較好地發展學生的數學思維。

三、以畫圖為抓手，發展抽象解題能力

數學學習要充分發揮幾何直觀在解決問題中的作用，注意引導學生利用幾何直觀把復雜問題轉化成簡單的問題，在直接利用直觀手段求解的過程中，幫助學生不斷積累利用直觀進行思考的經驗，發展抽象解題的能力。如人教版一年級下冊《100以內數的認識》中有這樣一個問題：“28個橘子，9個裝一袋，可以裝滿幾袋？”

有人會認為這是一道有余數的除法，非一年級的學生所能解決。其實，教材編排的目的是要激發學生的探究欲望，用所掌握的知識和方法，進行解決新問題的嘗試。

（一）模擬情境，幫助學生探究解題思路

師：小朋友們可以用28個小圓片來表示橘子，數一數，分一分。

通過動手操作，幫助學生理解條件和問題，為解決問題積累活動經驗。

（二）以畫圖為引導，實現解法的多樣性

師：你能用我們學過的方法，如畫圖、畫表格或其他你喜歡的方式清楚地把自己分橘子的過程表示出來，讓大家都能看明白嗎？

學生很自然地想到用圈一圈的方法，即把9個橘子圈在一起，表示1袋。

（1） 圈一圈。

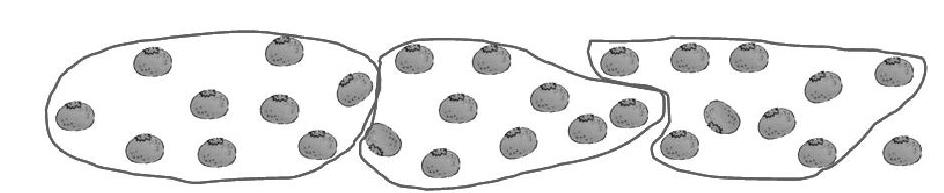
此圖已經直觀地展示了要求的結果，即可以裝3袋，還多出1個。

師：多出來的橘子還能再裝一袋嗎？

生（理直氣壯）：不能！

師：說說你的理由！

生：才多出1個橘子，怎么裝呀？

生：不到9個。

此題被一年級的小朋友輕松解決，幾何直觀顯示了其強大的力量，它可以不用列式，直接獲得答案。如果用有余數的除法去解決這個問題，一年級的小朋友根本無法理解，而通過圈一圈、畫一畫，讓數學變簡單了，這也為以后學習有余數的除法做了鋪墊。另外，教師巧妙地提出一個問題：“多出來的橘子還能再裝一袋嗎？”為學生理解余數要比除數小埋下伏筆。

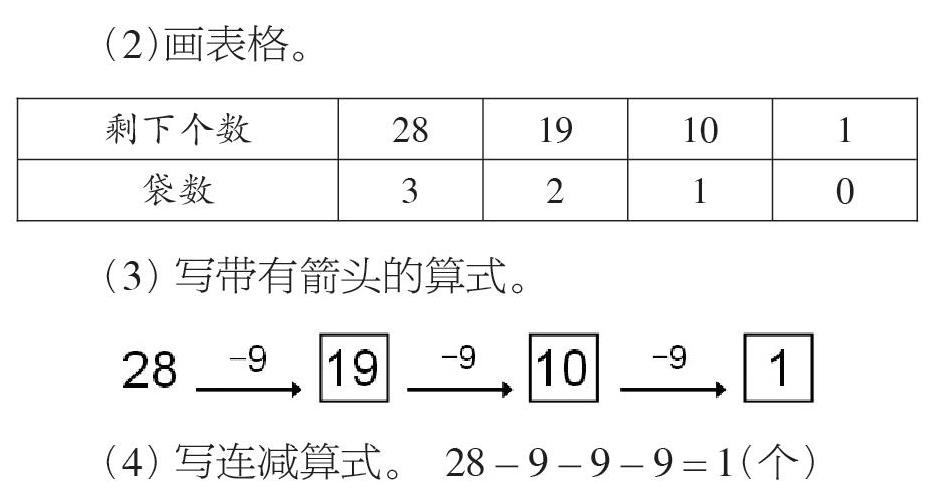
畫表格，畫箭頭，寫算式，解法越來越抽象，是幾何直觀幫助學生寫出了連減算式。隨著年級的升高，有些算式也要靠幾何直觀來理解。

總之，畫圖有助于發現、描述問題，有助于探索、發現解決問題的策略，也有助于理解和記憶得到的結果。用畫圖思考是學習數學的重要途徑。在教學過程中，遇到難以理解、產生困惑、不能解決的問題時，可讓學生畫一畫、想一想。讓畫圖解題不僅成為教學的一種方法，更是一種意識。在這種思想與方法的引導下，教師教得簡單，學生學得輕松。

參考文獻：

[1] 義務教育數學課程標準（2011年版）解讀[M].北京：北京師范大學出版社，2011.

[2] 吳正憲.吳正憲給小學數學教師的建議[M].上海：華東師范大學出版社，2012.

[3] 戴曙光.簡單教數學[M].上海：華東師范大學出版社，2012.

[4] Israel E.Drabkin.Aristotles Wheel：Notes on the History of a Paradox. Osiris，Vol.9.（1950）：162～198.

（浙江省杭州市經濟技術開發區江灣小學 310018）