幾何直觀，化無形為有形

趙薇萍

【摘 要】低段學生的年齡特點決定了他們對以形象為表征的素材的認可，所以，教師在教學中以幾何直觀為切入口，就能化無形為有形，這是符合他們的認知規律的。對此，教師要充分利用幾何直觀進行教學，把抽象的知識具體化，把具體的事物抽象化，才能叩開學生思維的大門，全面提升學生的核心素養。

【關鍵詞】幾何直觀；數形結合；模型思想；鏈接生活；類比推理

數學理性而抽象，對于以直觀形象思維為主的低年級學生來說，學習抽象的數學并不是一件輕松的事。所以我們要“投其所好”，找準切入口，正確引導，使數學成為一門看得見摸得著的接地氣的學科。兒童的年齡特點決定了對于以形象為表征的素材的認可，所以以幾何直觀為切入口，就能化無形為有形，這樣做符合他們的認知規律。經過實踐，筆者認為利用幾何直觀進行教學是一種非常有效的方法。幾何直觀能力的孕育階段主要是指一、二年級。這個階段的兒童以動作思維、形象思維為主，數學學習很大程度上依賴于直觀教學，低年級的直觀教學主要借助實物、圖片、符號等直觀載體。所以“幾何直觀”中所指的“圖形”不僅局限于幾何圖形，運算符號、方框、箭頭等直觀的符號表示出的圖示語言，甚至用圖形、文字、字母表示的數量關系式都可以看成是一種“直觀”。針對低年級兒童的年齡特點和認知規律，運用幾何直觀教學，旨在通過學生熟悉的感性材料，幫助學生在頭腦中建立表象，給思維提供足夠的表象支撐，促進思考。行走于課堂和生活之中，筆者發現幾何直觀的素材俯拾皆是，只要做個教學的有心人，這些素材都能為我們所用。下面筆者談談自己的幾點做法。

一、數形結合，在畫一畫中感知關系

畫畫是孩子的天性，很多孩子很小的時候就喜歡“涂鴉”，如果讓孩子用畫筆畫出題意，就能使原先不明朗的數量關系躍然紙上，難題不攻自破，成功的愉悅感自然生發出來。在畫畫中學數學，這是孩子們樂意做的事。低年級畫形象的圖，隨著年級的升高，可以慢慢過渡到畫線段圖。畫畫運用數形結合的思想方法，用畫筆簡明扼要地畫出數量關系，符合學生的認知規律，讓學生在感知具體形象的圖形時，找到解決問題的突破口，從而達到化難為易的效果，以調動學生的積極性，提高學生的思維能力，獲得分析和解決問題的一些方法，進而培養學生綜合運用數學的意識。

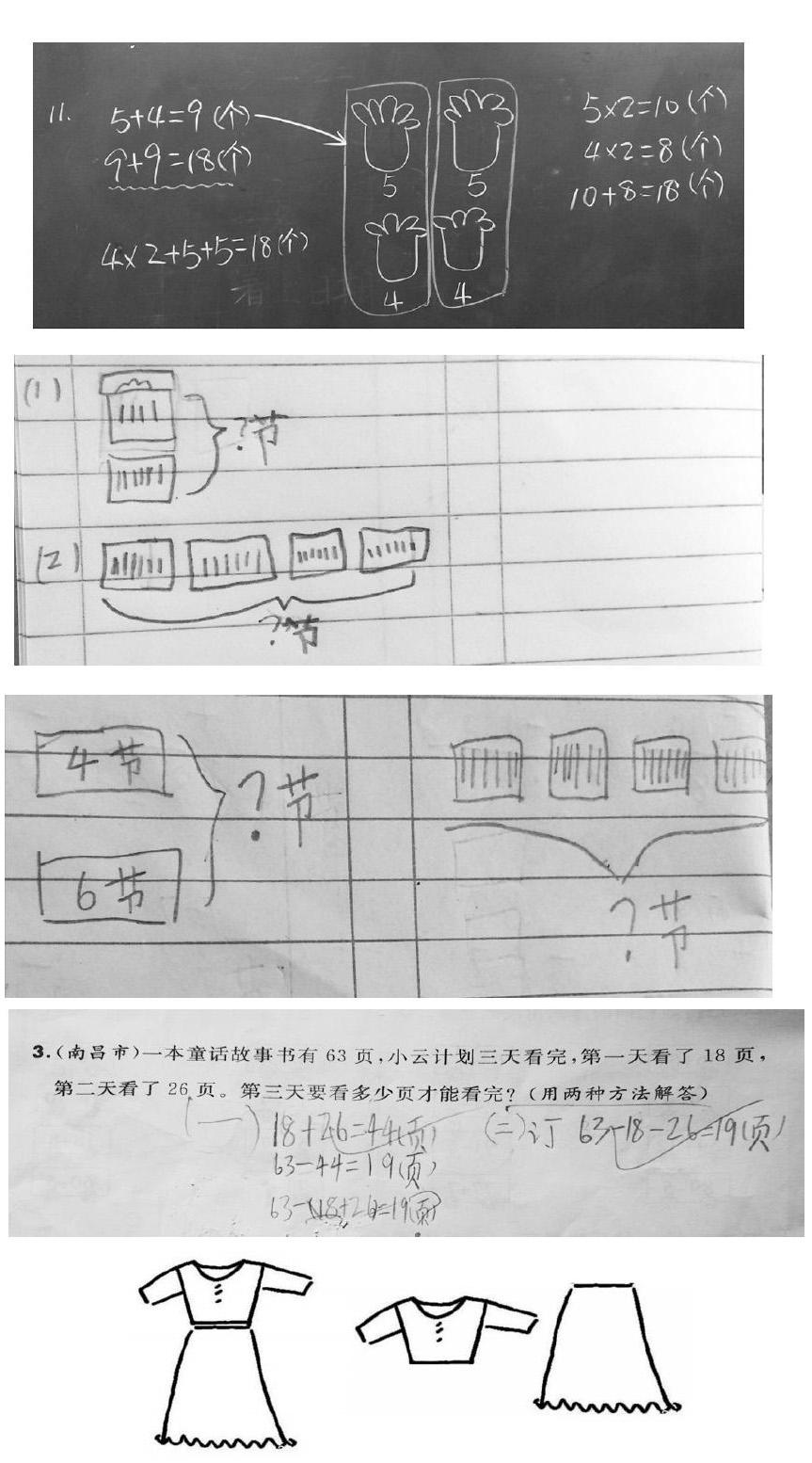
例如，二上教材中有這樣一道習題，一頭亞洲象每個前肢有5個腳趾，每個后肢有4個腳趾，這頭亞洲象一共有多少個腳趾？有些學生不理解。教師可指導學生仔細閱讀后在黑板上畫出了大象的腳印，當抽象的文字變成形象的圖畫時，學生思維的火花會被點燃，能想到不同的計算方法。

又如，超市里的7號電池有一板裝4節的，也有一板裝6節的。（1）兩種電池各買一板，一共多少節電池？（2）如果買4板6節裝的，一共是多少節電池？這道習題蘊含兩種數量關系，有的學生厘不清，可以啟發他們先畫圖，再解答。

再如，三上學習倍的知識，初步認識兩個量之間的倍數關系后，可以要求學生畫一畫，畫出相互之間的倍數關系，就能促進對知識的理解和深化。比如第一行畫3個圓，第二行畫三角形，要求三角形的個數是圓的2倍；第一行畫5個正方形，第二行畫的正方形是第一行的2倍；你還能創造其他的2倍關系嗎？最后的開放題其目的是使學生理解兩個量不管怎么變，相互之間的關系始終是2倍。

畫圖，對某些學習能力較弱的學生來講，更像一根拐杖。借助這根拐杖，才能掃清思考的障礙。

二、鏈接生活，在比一比中明白算理

數學來源于生活，又應用于生活。低年級的學生已經有了一定的生活經驗，如果能把課堂中的數學和生活中的情境鏈接起來，就能變得生動形象、妙趣橫生。把課堂中嚴肅的數學和生活聯系起來，數學教師要改變過去那種板起臉孔說話、語言呆板枯燥的陋習，充分發揮語言的作用，語言既要準確嚴密，又要力求聲情并茂、幽默風趣，這樣才能使學生聽起來輕松而又記憶深刻，在數學教學中適當采用“比喻”，會收到意想不到的效果。比如解決問題，用兩種方法解答，學生往往會把分步列式和綜合算式當成兩種方法，如下題。

可以給學生打個比方，這兩種方法好比同一套衣服，有時分開穿，有時合起來穿，不管是分開穿還是合起來穿，衣服是同一套，所以方法還是同一種。兩種方法就是需要兩套不同的衣服，所以解題思路必須不一樣。

比如，兩個問題的題目，第一問已經算出來的數據，第二問可以直接拿來用，不必再算一遍，可有些學生還是會從頭算，如下題。

可以給學生打個比方，從教室的這一頭走到那一頭去，分兩次走，走到一半停下來，第二次可以繼續接著走，不必再從頭走起。這種不利用已求出的數來列式的方法相當于路走了一半又回到起點再從頭開始。如果在教室里演示一遍，效果更佳。學生覺得生動有趣，通俗易懂的道理就深入其中。

比如，（）÷2=6 （）÷6=6，有不少學生做成（3）÷2=6，（1）÷6=6 ，碰到這種情況，教師可以用班級里學生的姓名打比方。如楊潤小朋友犯了那樣的錯，教師指導學生分析錯誤后，可以開個善意的玩笑：“楊潤可不可以叫潤楊啊？”教室里會蕩起一片歡樂的笑聲。

經過打比方，枯燥的道理化解在淺顯易懂的直白的語句中，平面抽象的數學道理就變得立體豐滿起來了。把生活中有趣的因子提煉出來，讓學生在輕松愉悅的氣氛中學習，知識更易于理解。做個有趣的教師，讓學生親其師而信其道。良好的課堂氣氛不是鴉雀無聲，而應是充滿笑聲，學生在一堂課中感受的不是壓抑和沉悶，而應是輕松和愉快。

三、操作表演，在動一動中理解題意

培養目標自從雙基轉成四基以來，教學過程中，我們更注重數學基本活動經驗的積累了。學生手腦并用，才能更深入地理解概念的含義。數學教學本質上應該是一種數學活動的過程，重在操作，離開教學活動過程，數學方法也就無從談起。如等分除和包含除，可以讓學生通過擺小棒來區別，等分除是已知總數和份數，所以要按份數擺放，可以一根一根地分，也可以兩根兩根地分……分完有多出來接著再分；而包含除是已知總數和每份數，所以必須按每份的要求，一份一份地分。

比如，三下辨認方向這一內容，要求給定東南西北四個方向中的一個，能辨認其他方向。很多學生能按“上北下南，左西右東”來判斷。可是如果不是面向北方，而是面向東方或面向西方，讓學生說出左邊是什么方向，右邊是哪邊，他就暈頭轉向了。筆者設計了一個“轉轉轉”的游戲，每人畫一個標準的方向圖，再根據要求轉，操作很方便。如早晨起來，面向太陽，左邊是（）方，右邊是（）方。就可以把這個方向轉動一下，把東方朝上，就可以看到左邊是北，右邊是南了。就像汽車的方向盤，可以根據要求任意轉動。

又如，有這樣兩道題：（1）三個孩子相互握手，共握了幾次手？（2）阿姨和三個客人都握手，一共要握幾次手？這兩道貌似相同的握手題目，實則條件不一樣，如果請兩組同學來表演一下，內在區別就顯而易見了。

因此，教師在教學中要創造機會讓學生在活動中去體驗，不斷形成自身的實踐經驗，加深對問題的認識，產生認識、情感、行為的變化。

四、動手拼組，在玩一玩中培養創意

幾何直觀是一切幾何學的基礎。小學數學中的幾何學主要訴諸兒童的直觀感受，借以識別各種不同幾何圖形。由于小學生的認知水平還處于“具體運算階段”，認識幾何圖形主要通過動手操作，進而積累對這些圖形的經驗，獲得感知。小學幾何的主要目標是“積累幾何活動經驗，發展幾何直觀，初步感受幾何推理的魅力，體會幾何的美”。

例如，一下“認識圖形”這一內容，要求能辨認長方形、正方形、三角形、平行四邊形和圓等簡單圖形，會用這些圖形拼圖。教師要創造條件讓學生充分活動，觀察圖形的特點，并在圖形的拼組中體會圖形之間的關系。比如“用七巧板拼三角形，看誰拼得多”這節課，一開始可以讓學生用其中的兩塊或三塊拼，逐步提高要求，如用七巧板先拼成一個三角形，然后想最少移動幾塊變成長方形、正方形、平行四邊形、梯形……經過操作學生會發現，每次用七塊板拼一個常見的平面圖形，想變形，不需要打亂重拼，而是移動其中的一小部分就可以變成另外的圖形，圖形之間是可以互相轉化的。比如正方形變長方形，最少移動兩塊，再移動一塊變成平行四邊形，移動一塊變三角形，移動一塊變梯形。最后讓學生自由發揮，愛拼什么就拼什么。給學生插上想象的翅膀，你會發現他們的想象力令人驚嘆。

正是在這玩一樣的拼圖中，學生建立起了初步的空間觀念，領略了數學的美。教學中，如果教師慢下來，放手讓學生自由發揮，他們無限的創意，會帶來別樣的驚喜。

五、類比推理，在想一想中建立模型

類比推理亦稱“類推”，它是指根據兩個對象在某些屬性上相同或相似，通過比較而推斷出它們在其他屬性上也相同的推理過程。它是從觀察個別現象開始的，因而近似歸納推理。但它又不是由特殊到一般，而是由特殊到特殊，因而又不同于歸納推理。

我們可以用類比的方法幫助學生把知識串聯起來。比如，二上數學廣角，學習排列和組合，例題1是用三張數字卡片擺不同的兩位數，學生通過擺數字卡片都可以有序擺出兩位數。

但是如果換一下題目，有些學生又不知道了，比如“有3本不同的書，要送給兩個人，有幾種不同的送法？”可以問學生：這道題和我們學過的哪道題思考方法一樣？這時，學生就會把這兩道題聯想到一起，這三本書就相當于三張卡片，送給兩個不同的人就相當于擺不同的兩位數。

這好比是同一個人，穿了兩件不同的衣服，衣服換了，但人沒變。我們要透過現象看本質，同一類題，可以用同樣的方法去思考。還是這個人，你能給他換上其他漂亮的衣服嗎？于是學生紛紛開動腦筋，編出了很多這類題。如姐姐和妹妹想吃水果，現在有一個蘋果、一個梨和一個橘子，有幾種不同的分法？

又如今天早餐的飲料有牛奶和豆漿，主食有饅頭、面包和面條，選一種飲料和一種主食，有幾種不同的選法？

這里的1、2、3三個數可以對應三本書、三個水果、三種主食……個位和十位分別對應兩個人、兩種飲料……這個內容的學習有助于學生初步形成模型思想，提高學習數學的興趣和應用意識，模型思想的建立是學生體會和理解數學與外部世界聯系的基本途徑。這個過程就是一個建模的過程，去偽存真，抽絲剝繭，簡化了教學內容的形式，把握了教學內容的本質。

綜上所述，幾何直觀是指憑借圖形的直觀性特點，將抽象的數學語言與直觀的圖形語言有機地結合起來，整合抽象思維與形象思維，充分展現問題的本質，突破數學算理上的難點。由此，幾何直觀于學生而言，是一種有效的學習方式；于教師而言，是一種有效的教學手段。它是數形結合思想的體現，在小學數學教學中是不可缺少的、重要的數學思想方法。幾何直觀降低了低年級學生的學習難度，化抽象為形象，化無形為有形，幫助學生輕松開啟數學的探究之旅。

（浙江省寧波市北侖區大碶博平小學 315800）