談初中數學教學中函數思想的滲透

胡連成

【摘要】 在新課改的背景下，初中數學課堂教學進行數學思想特別是函數思想的滲透，對于推動課堂教學改革，提高教師素質，培養學生創新能力有著積極的意義，而如何實現這一目的是數學教師應該認真考慮的問題.

【關鍵詞】 數學教學；思想方法；函數思想

日本數學教育家米山國藏在其著作《數學精神、思想和方法》一書的序言中寫到：“學生在初中、高中接受的數學知識， 出校門不到一兩年，很快就忘掉了，然而，不管他們從事什么業務工作，唯有深深銘刻于頭腦中的數學精神，數學的思維方法、研究方法、推理方法和著眼點，卻隨時隨地的發揮作用，使他們受益終生. ”

數學思維蘊含于數學思想之中，數學思想蘊含于數學知識、數學方法和技能技巧之中. 數學思想使數學內容形成統一的和諧. 新的《課程標準》突出強調：“在教學中，應當引導學生在學好概念的基礎上掌握數學的規律（包括法則、性質、公式、公理、定理、數學思想和方法）”. 函數是中學數學的重要內容，運用函數思想可以解決很多數學問題. 因此教學中應重視函數思想的滲透.

一、用運動變化觀點歸納知識形成體系

許多數學知識表面上是孤立，只要我們從運動變化的觀點去觀察分析，就不難發現它們的內在聯系，從而把零碎的知識變成一個統一的整體，使理解深化.

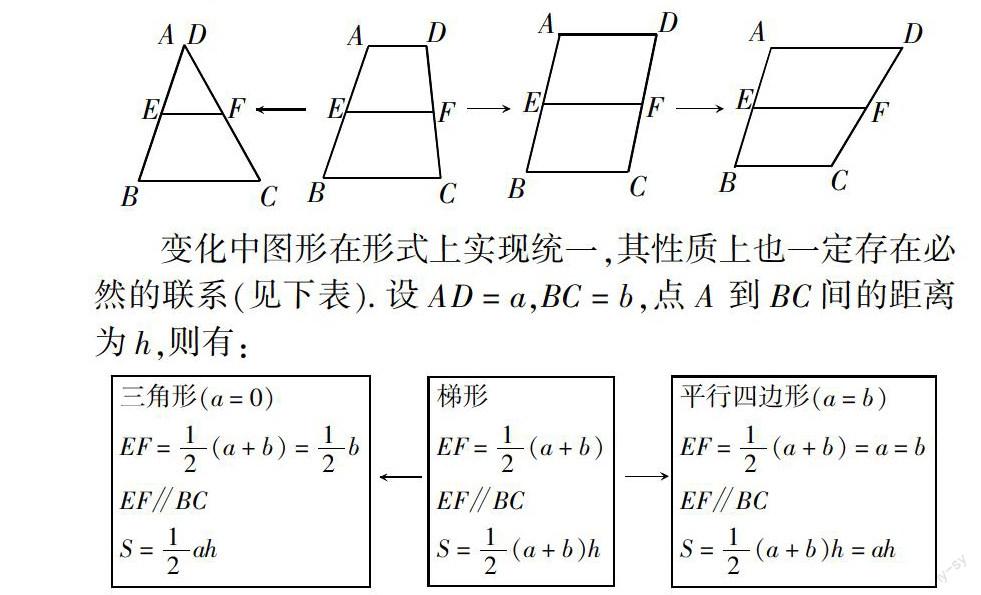
例1 三角形、平行四邊形和梯形（如下圖）可以這樣理解：當梯形ABCD的頂點D，在直線AD上向左運動至點A時，梯形變為三角形；當點D向右運動時，梯形依次變為平行四邊形、梯形.

變化中圖形在形式上實現統一，其性質上也一定存在必然的聯系（見下表）. 設AD = a，BC = b，點A到BC間的距離為h，則有：

揭示運動變化規律最好的工具就是函數. 人類對函數的認識經歷了 “變量說”、 “對應說（映射說）”、 “關系說”三個階段. 可以說，函數概念的靈魂是運動變化、是變量間的對應關系. 函數思想就是串起知識項鏈的主線，它不僅是數學研究的對象，也是解決現實問題常用的一種方法. 函數思想廣泛地滲透到數學學習的全過程，不僅數軸、有理數與實數的概念和運算、式的運算及恒等變形、方程與不等式等蘊含著函數思想，而且圖形的變化、性質之間的關系也和函數思想存在著一定的聯系，函數的重要性不言而喻.

二、注重運用函數思想解決問題

在數學解題中，以函數思想為主導，運用函數方法，結合具體函數的性質，可以使很多數學問題轉難為易、化繁為簡，是一個很重要的解題策略思想，人們統稱為函數法.

例2 （14年天津市第12 題）已知二次函數y = ax2 + bx + c（a ≠ 0）的圖像如圖，且關于x的一元二次方程ax2 + bx + c - m = 0（a ≠ 0）沒有實數根，有下列結論：

① b2 - 4ac > 0；② abc < 0；③ m > 2. 其中，正確結論的個數是 （ ）.

A. 0 B. 1 C. 2 D. 3

分析： ①②借助函數圖像比較容易解決，③的判斷難度較大，要注重方程與函數的聯系：

一元二次方程ax2 + bx + c - m = 0沒有實數根，則可轉化為ax2 + bx + c = m，即可以理解為y = ax2 + bx + c和y = m沒有交點，即可求出m的取值范圍.

三、運用函數思想進行教學設計

教師采取教學方法、教學程序的有效性取決于是否體現了數學思想方法的靈魂作用，沒有數學思想指引的課堂是膚淺的、是不利于學生思維發展的. 對學生未來發展起決定作用的不是掌握知識的多少而是解決實際問題策略選擇，蘊含數學思想的教學可以培養學生靈活有效的思考問題、解決問題，潛移默化的影響學生的將來發展. 因此，在數學思想中起著統領作用的函數思想理所當然在數學教學要發揮重要的指導作用.

例3 學習“倒數”時，教師可以從三個層次加以引導.

1. 了解倒數的定義的基礎上會求一個非0實數a的倒數.

2. 理解一個非0實數a的倒數仍為實數，感受數a與它的倒數是一對一對應關系.

3. 進一步思考當數a（a > 0）增大時，■將隨之減小；當數a（a < 0）規律相同.

教學如果僅停留在第一層次，那就是單純傳授知識的教學，學生只是掌握了倒數的求法，而在思維上沒有得到發展. 只有把學生對倒數的理解引導二、三層次，從嶄新的角度去理解問題，才能真正培養學生的數學思維能力.

數學知識之間相互聯系、相互滲透，從而豐富了人們對問題的認識. 為了培養學生數學學習中的運算能力、邏輯推理能力、空間想象能力及綜合運用數學知識解決問題的能力，學生在學習中不但要養成用聯系觀點歸納知識，還要有意識地運用函數思想方法去解決實際問題. 函數思想是中學數學重要的數學思想，教師教學中注重發揮函數思想的指導作用，讓數學知識逐漸內化為學生的數學素質.

【參考文獻】

[1]季素月，王力耕，尤善培.給數學教師的101條建議，南京師范大學出版社，2005.9.