幾何畫板在中學數學教學中的應用

楊鳳武

【摘要】當前，幾何畫板在高中數學教學中的應用日益普遍，它不僅能夠幫助學生創設良好的教學情境，也能夠幫助學生動態地觀察、探索和發現空間結構和數量關系，增進對知識點的理解和把握.本文試圖結合自身教學經驗，對幾何畫板在高中數學教學中的應用進行探討.

【關鍵詞】幾何畫板;高中數學;應用

引 言

隨著信息技術的迅猛發展，人們生活與工作的方式也發生了深刻變化.教學方式在信息技術的發展浪潮中也得到了巨大的變革.在高中數學教學中，幾何畫板正以其靈活方便的操作方式，強大的圖形和圖像轉換功能，成為中學數學課件制作的重要軟件.幾何畫板在數學教學中所發揮的作用是無窮的，一方面，它能夠動態地展現知識的發展歷程，讓學生感受數學的動態美;另一方面有助于數學實驗課的開展，為數形結合的思想搭起了橋梁，幾何畫板運用到高中數學教學中的確意義非凡.

一、幾何畫板的概念介紹及作用分析

幾何畫板（The Geometers Sketchpad）是一個適用于數學、平面幾何、物理的矢量分析、作圖、函數作圖的動態幾何工具，它能夠提供豐富而方便的創造功能使用戶可以隨心所欲地編寫出自己需要的教學課件.幾何畫板的功能強大，利用幾何畫板不僅能夠畫出各種歐幾里得圖像，對于任何給出的函數表達式都能畫出它的圖形，還能夠變換畫出圖形和圖像，進行圖形反射、縮放、平移等操作以及進行測量、計算等.幾何畫板具有操作簡單、便于學習，動態演示、便于理解，空間自由、形式多樣，準確無誤、探索性強等多種有點，它的出現，對于改進高中數學教學方法，提高數學教學效率有重要作用.

首先，幾何畫板能夠幫助教師教學.新課程改革要求教師能夠結合學生特點和教學內容的重難點，適當使用多媒體課件來輔助教學，通過直觀的圖形和動態教學視頻，化難為易，花抽象為具體，便于學生掌握和理解.幾何畫板簡單易懂，功能強大，尤其是在動態研究數學方面具有無與倫比的優勢，利用幾何畫板能夠方便、迅速地制作出很多數學課件，演示直觀、動態的畫面去幫助學生掌握抽象、無味的數學定理、公式和法則非常有用，學生也能更深刻地體會和理清知識之間的相互關系.因此，幾何畫板必然成為提高數學教學效率的有力工具.

其次，有利于提高學生學習興趣.高中數學由于知識結構復雜，理論深奧抽象，很多學生學習起來比較吃力，這導致很多學生不愛學，上數學課不專注.學生通過親自運用幾何畫板，可以使原來枯燥乏味的數學變得生動形象，許多抽象難懂的問題變得形象具體了，這樣有助于增強學生學習數學的興趣.例如平面解析幾何由于比較抽象，運算量大，使很多人感到學起來困難.教師在課堂上運用幾何畫板在課堂上動態演示，鼓勵學生積極利用幾何畫板，對圓錐曲線的定義與性質進行操作，通過合作、交流、研究，學生即能深刻地理解圓錐曲線的相關知識.

最后，有助于教師開發校本課程.校本課程即以學校為本位、由學校自己確定的課程，高中數學新課程改革要求教師開發校本課程來適應學生群體的互異性和多面性.幾何畫板對于幫助教師開發校本課程具有重要優勢，它可以通過將小學乃至初中數學中最基本的知識聯系起來，幫助學生鞏固以前所學，全面掌握公式、公理、法則的來龍去脈，使學生擴展數學知識結構體系的縱深度.

二、幾何畫板在高中數學教學中的應用分析

本文以二面角的平面角的概念學習為例來談一談幾何畫板在高中數學中的應用.

二面角的平面角的概念是“二面角”這節內容的重點和難點，教師需要應用幾何畫板來對其本質內容進行深入分析.

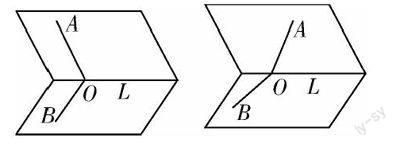
1.創設情境：利用幾何畫板上設計下圖所示的二面角α-L-β，將射線OA，OB分別在兩個平面上拖動.請學生思考，當二面角α-L-β確定以后，如何確定二面角的平面角 AOB的大小呢？

2.通過改變 OA與OB的位置，使 OA，OB與L之間形成定角.那么這個定角多大才能反映兩個半平面的張合程度呢？通過幾何畫板的動態演示，學生不難發現，當 OA，OB都與L垂直時，最能說明二面角的大小.

3.形成概念：通過幾何畫板的演示，學生很容易得到二面角的平面角的概念.

幾何畫板在函數教學中也有重要作用.“函數”是中學數學中最基本、最重要的概念，函數的表達方式包括解析式和圖像兩種，在實際教學中常常需要相互對照來學習.教師可以利用幾何畫板根據函數的解析式快速作出函數的圖像.

三、結 論

實踐證明，幾何畫板在高中數學教學中的應用能夠通過創新教學模式，化抽象的理論知識為直觀具體的演示圖像，幫助學生理解概念，培養學生的空間探索發現能力，對于幫助學生理解，建構數學知識結構體系，提高數學教學效率有重要作用.但是我們也應該看到，幾何畫板在高中數學教學中的應用仍然存在很多問題，教師應加大對幾何畫板研究及應用的重視，進一步提高高中數學教學效果.

【參考文獻】

[1]楊帆.信息技術與高中數學教學的整合[D].東北師范大學，2012.

[2]張文梅.幾何畫板對初中學生幾何動態問題解決的有效性探索[D].華東師范大學，2010.