略談數學眼光及其培養

李樹臣

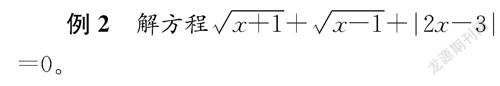
摘要：作為數學核心素養的構成，“三會”是數學教育的終極目標。其中，數學眼光是生發于數學學科特性視角的一種思考，關注的是“數學是研究數量關系和空間形式的科學”的內涵，彰顯的是“思想材料的形式化抽象”的特點，主要就是在現實與數學之間進行的思維切換。根據數學眼光的主要表現，其培養可以有側重地從四個維度展開：增強創新意識，發展空間觀念，重視幾何直觀，提升抽象能力。

關鍵詞：數學眼光;創新意識;空間觀念;幾何直觀;抽象能力

《義務教育數學課程標準（2022年版）》明確將“會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界”（統稱“三會”，分別簡稱“數學眼光”“數學思維”“數學語言”）作為數學核心素養的構成，并做了比較詳細的解釋——相比之下，《普通高中數學課程標準（2017年版2020年修訂）》只是提出“三會”，并沒有解釋它（包括它與數學核心素養的關系）。作為數學核心素養的構成，“三會”是數學教育的終極目標。本文談談筆者對數學眼光及其培養的認識與思考。

一、對數學眼光的一些認識

觀察是人們認識世界、獲取知識的重要途徑，也是科學研究的重要方法。巴甫洛夫告誡學生“不學會觀察，你就永遠當不了科學家”，并把“觀察、觀察、再觀察”作為自己的座右銘。觀察是通過“看”和“思考”進行的，觀察是科學研究中的一個基本方法，在數學學習中有著重要的方法論意義。

數學眼光是生發于數學學科特性視角的一種思考，關注的是“數學是研究數量關系和空間形式的科學”的內涵，彰顯的是“思想材料的形式化抽象”的特點，主要就是在現實與數學之間進行的思維切換。胡晉賓，劉洪璐.數學眼光的內涵及培養[J].中學數學月刊，2021（2）：1720。

具有數學眼光的人在面臨現實情境時，通過觀察、分析、思考等活動能透過事物的表面現象抽象出相關的數學知識;而一旦提到某個具體的數學知識時，也會自動地想到現實中的具體案例。胡晉賓，劉洪璐.數學眼光的內涵及培養[J].中學數學月刊，2021（2）：1720。

例1今有兩個容量為100 mL的酒杯，分別盛有50 mL白酒和50 mL紅酒。從白酒杯中用10 mL的取酒勺取一勺倒入紅酒杯中（第一次動作），使之充分混合，然后從紅酒杯中取一勺混合酒倒入白酒杯中（第二次動作）。請問：白酒杯中所含的紅酒與紅酒杯中所含的白酒一樣多嗎？為什么？

這是筆者在學生學習了分式的知識后設計的一個問題。對此，很多學生嘗試利用分式的知識，通過計算加以比較：第一次動作后，白酒杯中含白酒40 mL，紅酒杯中含紅酒50 mL、白酒10 mL;第二次動作后……計算遇到了困難。實際上，這個問題雖然通過計算完全能夠給出判斷，但是，解答過程涉及“溶液、溶質、濃度”等初三化學知識，而且計算過程比較復雜。

教學中，筆者設計了以下子問題，引導學生理解問題的實質。

（1）第二次動作后，兩個杯子里都是混合酒，各有多少？

（2）白酒杯中含有的白酒還是50 mL嗎？少的白酒哪里去了？

（3）白酒杯中多的紅酒是哪里來的？

（4）白酒杯中少的白酒和多的紅酒，從量上看一樣嗎？

學生圍繞這四個子問題，通過分析、思考、討論、交流發現，“最后白酒杯中所含的紅酒數量等于紅酒杯中所含的白酒數量，因為，兩個酒杯中酒的總量不變，某個酒杯中少了的酒被另一個酒杯中少了的酒填上”。發現這個結論（數量關系或數學模型）是思辨的結果，而不是用算法得到的程嶸，練冬蘭，廖運章.高中生解決數學應用題策略及表征偏向的調查研究[J].教育研究與評論（中學教育教學），2018（7）：4148。，需要具有敏銳的數學眼光：以整體、抽象（可輔以直觀、形象）的新視角看到復雜變化中的簡單不變（問題的本質）。

進一步地，我們不妨用斯托利亞爾和弗賴登塔爾的理論來認識數學眼光。斯托利亞爾認為，“數學教學應該是數學活動的教學”，并且指出數學活動可以分為三個階段：“第一，經驗材料的數學組織化;第二，數學材料的邏輯組織化;第三，數學理論的應用。”A.A.斯托利亞爾.數學教育學[M].丁爾陞，等譯.北京：人民教育出版社，1984：7。弗賴登塔爾認為，“數學地組織現實世界的過程就是數學化”弗賴登塔爾.作為教育任務的數學[M].陳昌平，唐瑞芬，等編譯.上海：上海教育出版社，1995：1。，并且指出數學化可分為橫向（水平的）數學化和縱向（垂直的）數學化兩個層次，橫向數學化關注生活與數學的聯系（包括從現實世界到數學知識、從數學知識到實際問題），縱向數學化關注數學知識內部的遷移與調整（從數學到數學）。數學眼光主要發生在橫向數學化這個層次（或者數學活動的第一個階段）。一個人的數學眼光與其具有的知識技能、積累的活動經驗以及聯系實際的意識與能力等因素有關。具有數學眼光的人，在經歷這個層次的過程中形成了數學概念、法則、定理、規律，以及為解決實際問題而構造了數學模型等。

二、對培養數學眼光的幾點思考

作為數學核心素養的構成，數學眼光主要表現為創新意識、空間觀念、幾何直觀與抽象能力。中華人民共和國教育部.義務教育數學課程標準（2022年版）[S].北京：北京師范大學出版社，2022：5。它們之間并不是完全獨立的，有一定的交叉，尤其是創新意識和其他三種表現。因此，數學眼光的培養可以有側重地從以下四個維度展開。

（一）增強創新意識

創新意識主要是數學眼光靈活、獨到的表現。具有創新意識的人，往往思路開闊、富于聯想，具有較強的直覺思維、發散思維能力，并且能夠獨立思考，敢于質疑問難。教學中，應該精選一些非常規問題、開放性問題，鼓勵、引導學生經歷觀察、思考、聯想、猜測等活動，在活動過程中打破常規，從新的角度或方向大膽探索，從而逐步學會把已知知識、方法廣泛、迅速地遷移，靈活、變通地運用到新情境中去。久而久之，學生的創新意識將會得到增強，并逐步發展成為“數學慧眼”。

顯然，上述例1可以增強學生的創新意識。這里再舉一個簡單的例子。

例2解方程x+1+x-1+|2x-3|=0。

這是筆者在學生學習了算術平方根的知識后設計的一道題目。此題不需要通過計算來解答，而是可以打破解方程的常規，從算術平方根和絕對值的性質的角度迅速作出無解的判斷。

（二）發展空間觀念

空間觀念主要是指對空間物體或圖形的形狀、大小及位置關系的認識;有助于理解現實生活空間物體的形態、結構及運動變化，是幾何直觀的基礎，也是形成空間想象能力的經驗基礎。空間觀念實際上是一種“形感”，是數學眼光形象、可感的表現。圖形與幾何領域的知識大多是發展學生空間觀念的載體。教學中，應該精心設計問題情境，引導學生在觀察、實驗、猜測、推理等過程中，從感性到理性，完成對圖形與幾何領域概念與性質的感受、發現與梳理、總結。

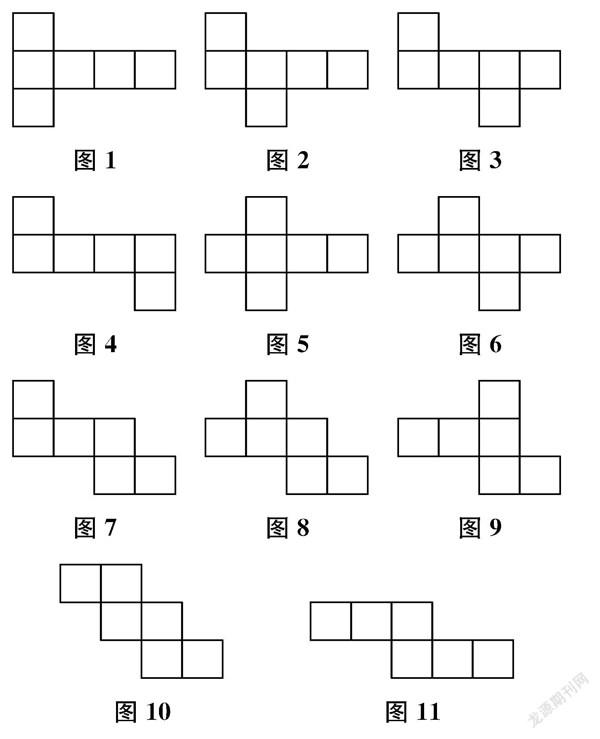
例如，學生學習“正方體的展開圖”時普遍感到困難，其根本原因在于空間觀念弱。對此，我們設計了系列學習活動，引導學生經歷“實驗探究—交流發現—歸類總結”的過程，系統掌握正方體的各種展開圖，充分發展空間觀念。

活動1觀察正方體紙盒有幾條棱，沿著其中的一些棱剪開，將正方體展開成平面圖形（保證六個面通過未剪開的棱連在一起）。

活動2組內交流共有幾種不同的展開圖，各組長依次把本組內不同的展開圖用膠帶貼在黑板上（與前面小組已有的展開圖重復的，就不要再貼了）。

活動3觀察黑板上不同的展開圖，思考有沒有重復和遺漏;如果沒有重復和遺漏，請將這些展開圖歸歸類。

通過上述活動，在教師的引導下，學生梳理、總結出正方體的展開圖共有11種情況，可以分為4種類型：（1）“一四一”型，如圖1—圖6所示;（2）“一二三”型，如圖7—圖9所示;（3）“二二二”型，如圖10所示;（3）“三三”型，如圖11所示。

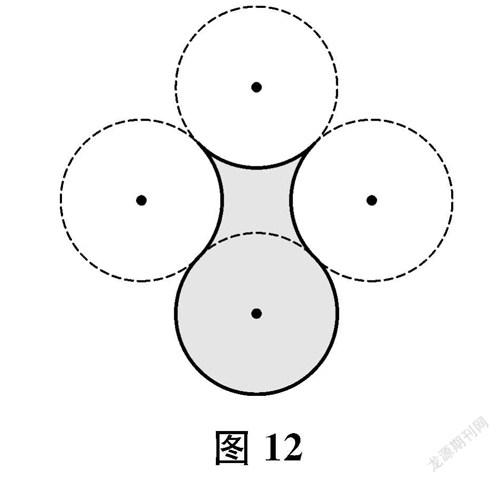
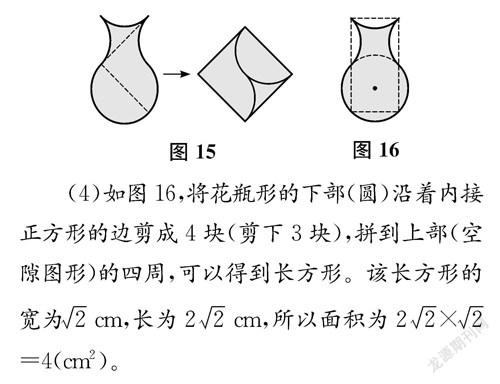
例34個半徑為1厘米的等圓的位置如圖12所示，其中陰影部分酷似一個花瓶的縱截面（不妨稱其為花瓶形）。你會計算花瓶形的面積嗎？

這是青島版初中數學九年級上冊在“36 弧長及扇形面積的計算”后設置的一個閱讀材料中的問題。此題以四個等圓按正方形的四個頂點“密鋪”為背景，考查學生將不規則圖形轉化為規則圖形來計算面積的能力。解此題的關鍵是發現“密鋪”的空隙圖形與一個圓的分割組合關系，能夠很好地發展學生的空間觀念，啟發學生的思維。同時，圖形設計精巧，可使學生感受到數學的對稱、和諧美。此外，解題方法具有開放性、多樣性，可以增強學生的創新意識。

教學中，可以引導學生觀察、實驗、猜測、驗證、推理、計算，從而（至少）得到以下四種解法：

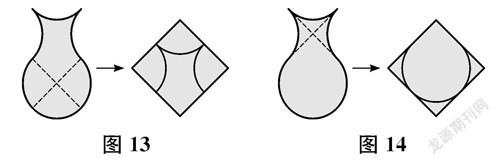
（1）如圖13，將花瓶形的下部（圓）沿著相互垂直的兩條直徑剪成4塊（剪下3塊），拼到上部（空隙圖形）的四周，可以拼成正方形。易知拼成的正方形的邊長等于圓的直徑，即2 cm，所以花瓶形的面積為2×2=4（cm2）。

（2）如圖14，將花瓶形的上部（空隙圖形）沿著相互垂直的兩條對稱軸剪成4塊（剪下3塊），拼到下部（圓）的四周，可以拼成正方形。易知拼成的正方形的邊長等于圓的直徑，即2 cm，所以花瓶形的面積為2×2=4（cm2）。

（3）如圖15，將花瓶形的下部和上部分別沿著各自的一條對稱軸（這兩條對稱軸相互垂直）剪成3塊，也能拼成正方形。易知拼成的正方形的邊長等于圓的直徑，即2 cm，所以花瓶形的面積為2×2=4（cm2）。

（4）如圖16，將花瓶形的下部（圓）沿著內接正方形的邊剪成4塊（剪下3塊），拼到上部（空隙圖形）的四周，可以得到長方形。該長方形的寬為2 cm，長為22 cm，所以面積為22×2=4（cm2）。

（三）重視幾何直觀

幾何直觀主要是指運用圖表描述和分析問題的意識和習慣，包括：感知各種幾何圖形及其組成元素，依據圖形的特征分類;依據語言描述畫出相應的圖形，分析圖形的性質;建立數與形的聯系，構建數學問題的直觀模型;利用圖表分析實際情境與數學問題，探索解決問題的思路。幾何直觀有助于把握問題的本質，明晰思維的路徑。教學中，應創設適當的問題情境，引導學生從實物中抽象出圖形，或根據語言描述畫出圖形，尤其是利用坐標思想或幾何意義將一些代數條件轉化為幾何圖形，并分析圖形特征與性質（包括其基本元素或其中基本圖形的關系），用它解決問題。孫紅強.圖形：培養直觀想象素養的關鍵要素[J].教育研究與評論（中學教育教學），2020（3）：5053。

例4兩人相繼在一張圓桌上擺放一枚同樣大小的硬幣（兩人手中都有足夠多的硬幣），誰放下最后一枚而使對方沒有地方再放，誰就獲勝。試問：是先放者獲勝還是后放者獲勝？怎樣才能穩操勝券？

本題以“在圓桌上擺放硬幣”的游戲為背景，考查學生對圓的中心對稱性的理解和應用。解答本題的關鍵是，運用幾何直觀，從實物中抽象出幾何圖形圓，充分利用圓的性質思考游戲的獲勝策略：假如圓桌小到只能放下一枚硬幣，當然是先放者獲勝;假如圓桌比較大，先放者只要把第一枚硬幣放在圓桌的中心位置，后放者每放下一枚硬幣，先放者只要把硬幣放在與后放者放的位置關于圓桌中心對稱的位置，即可穩操勝券。通過解答這個問題，學生不僅能加深對圓的認識，而且能培養幾何直觀的意識與能力。

在此基礎上，教師可以鼓勵學生思考更一般的情況：桌面不是圓形而是長方形或正方形的話，這種解答策略還有效嗎？從圖形的對稱性到游戲的對稱策略，學生能夠認識到對稱是一種重要的思維模式，從而自覺地運用對稱，思考、求解更多的問題。

（四）提升抽象能力

抽象能力主要是指通過對現實世界中數量關系與空間形式的抽象，得到數學的研究對象，形成數學概念、性質、法則和方法的能力，包括：從實際情境或跨學科的問題中抽象出核心變量、變量的規律及變量之間的關系，并用數學符號予以表達;從具體的問題解決中概括出一般的結論，形成數學的方法與策略。從本質上看，“抽象是從許多事物中舍棄個別的、非本質屬性，得到共同的、本質屬性的思維過程”史寧中.數學基本思想18講[M].北京：北京師范大學出版社，2016：10。;數學抽象是指舍棄事物的一切物理屬性，得到一個數學對象的思維過程。抽象是數學的本質特征之一，是數學的基本思想方法，并且是數學眼光深刻、犀利的表現。在數學知識形成及問題解決的教學中，都要讓學生經歷從現實到數學、從特殊到一般、透過現象看到本質等的數學抽象過程，從而提升數學抽象能力。

例如，教學一元二次方程的概念時，可以引導學生分層解決如下問題，從而經歷數學抽象的完整過程。

【從問題到方程】

（1）金星學校要用大小完全相同的240塊正方形地板磚鋪一個面積為60 m2的音樂教室。設每塊地板磚的邊長為x m，為了求出地板磚的邊長，可列方程：。

（2）《九章算術》中有一題：“今有二人同所立，甲行率7，乙行率3。乙東行，甲南行十步而斜東北，與乙會。問：甲乙行幾何？”意思是：“甲乙兩人同時從同一地點出發，甲的速度是7，乙的速度是3。乙向東行走，甲向南走了10步后向東北行走，與乙相遇。問：相遇時，甲乙分別走了多少？”設他們相遇時所用的時間為t，則相遇時甲共走了，乙共走了;為了求出相遇時，甲乙分別走了多少，可列方程：。

（3）一個兩位數，個位上的數字比十位上的數字小3，這個兩位數加上10后，恰好等于個位上的數字與十位上的數字之積的3倍。設個位上的數字為a，為了求出這個兩位數，可列方程：。

這一層次的三個問題體現了從現實情境到數學模型的抽象。其中的現實情境既包括當下的生活現實，也包括史料中的生活現實，還包括數學現實。未知數的設法既有直接設，也有間接設。學生分析題目中的數量關系，不難列出三個方程：（1）240x2=60;（2）（3t）2+102=（7t-10）2;（3）a+10（a+3）+10=3a（a+3）。

【從特殊到一般】

（4）將所列出的三個方程依次化為按字母次數降序排列的一般形式，得到4x2-1=0、2t2-7t=0、3a2-2a-40=0。這三個方程有什么相同與不同之處？

（5）上面這三個方程的本質屬性（相同之處）是什么？

這一層次的兩個問題體現了從特殊情況到一般概念的抽象。先引導學生尋找特殊情況的相同與不同之處（各種屬性），再引導學生保留相同之處（本質屬性），剔除不同之處（非本質屬性），從而建立一般概念。學生經過思考、交流，可以得到三個方程的相同與不同之處：（1）都含有一個未知數;（2）未知數有不同的含義;（3）未知數的最高次數都是2;（4）未知數的一次項和常數項可有可無。進而，可以根據三個方程的本質屬性，給出一元二次方程的概念：可以化為ax2+bx+c=0（x為未知數，a、b、c為常數，a≠0）形式的方程。

例5（2018年江西省中考試題）小賢與小杰在探究某類二次函數問題時，經歷了如下過程：

【求解體驗】

（1）已知拋物線y=-x2+bx-3經過點（-1，0），則b=，頂點坐標為，該拋物線關于點（0，1）成中心對稱的拋物線的表達式是。

【抽象感悟】

我們定義：與拋物線y=ax2+bx+c（a≠0）關于y軸上的點M（0，m）對稱的拋物線y′稱為拋物線y的“衍生拋物線”，點M稱為“衍生中心”。

（2）已知拋物線y=-x2-2x+5關于點（0，m）的衍生拋物線為y′，若這兩條拋物線有交點，求m的取值范圍。

【問題解決】

（3）已知拋物線y=ax2+2ax-b（a≠0）。

①若拋物線y的衍生拋物線為y′=bx2-2bx+a2（b≠0），兩條拋物線有兩個交點，且恰好是它們的頂點，求a、b的值及衍生中心的坐標;

②若拋物線y關于點（0，k+12）的衍生拋物線為y1，其頂點為A1;關于點（0，k+22）的衍生拋物線為y2，其頂點為A2……關于點（0，k+n2）的衍生拋物線為yn，其頂點為An（n為正整數）……求AnAn+1的長（用含n的式子表示）。

在學生學習了拋物線解析式的求法、一般式與頂點式的互化、頂點坐標以及開口朝向與大小（由什么決定）等知識后，筆者讓學生解決這道中考題。本題以二次函數相關知識為載體，新定義“衍生拋物線”的概念，分層設問，充分體現了從特殊到一般的抽象過程：不僅從第（1）問到第（3）問體現了解析式與對稱中心逐漸一般化的過程[第（3）問的第①小問還有一個逆向設計]，而且第（3）問的第②小問的解答也需要經歷一個從特殊到一般的過程（先求A1、A2，類推An、An+1）。多解決這類新定義、分層設問的問題，十分有利于學生提升閱讀理解能力以及數學抽象能力。