素養立意·創新取材·導向實踐

諸士金

摘? 要：“綜合與實踐”的題目可以考查學生所積累的數學活動經驗，數學應用意識和創新意識是評價數學學科核心素養的重要和有效載體. 文章從關注數學知識與方法的綜合、數學文化與知識的結合、數學思維與實驗的融合、數學與其他學科知識之間的聯系和數學與社會生活的聯系五個方面梳理了2021年各地“綜合與實踐”的典型中考試題，嘗試解讀了試題的命制意圖，并對2022年“綜合與實踐”中考復習提出適當建議.

關鍵詞：綜合與實踐;命題分析;核心素養

一、內容分析

2021年全國各地中考試題中“綜合與實踐”的考查內容和題型在延續往年試題風格的同時，稍有創新. 這里的創新源于近年來發展學生數學學科核心素養的理念滲透，也源于《義務教育數學課程標準（2011年版）》（以下簡稱《標準》）即將修訂的各種解讀. 從評價的角度來看，信度與效度較好的“綜合與實踐”的題目可以考查學生所積累的數學活動經驗，數學應用意識和創新意識是評價數學學科核心素養的重要和有效載體. 有利于引導一線教學導向不唯題做題，而要實實在在地開展以理解教學為基礎、以理解學生為主體、以理解數學為本質的數學教學活動. 讓學生親歷實踐、探究、體驗、反思、合作、交流等學習過程，綜合運用數學學科和跨學科的知識與方法解決現實世界的數學問題.

2021年各地“綜合與實踐”的中考試題突出關注數學知識與方法的綜合、數學文化與知識的結合、數學思維與實驗的融合、數學與其他學科知識之間的聯系，以及數學與社會生活的聯系. 綜合考查了學生的直觀想象與數學抽象、邏輯推理與數學運算、數學建模與數據分析這六個方面的核心素養. 下面結合部分試題從考查內容的角度進行分類，對“綜合與實踐”與核心素養評價的立意進行分析.

二、命題思路分析

1. 關注數學知識與方法綜合的考查

從概念到判定，從判定到性質，從性質到應用，數學知識之間有著知識結構前后一致、思想方法邏輯連貫的特征. 因此，數學知識的學習是一種學生在已有認知結構的基礎上主動認識數學知識結構，并重新建構形成新認知結構的過程. 因此，對學生在數學知識、數學方法上的學習效果和建構的認知程度的評價需要設置結構優良、信度與效度較好的綜合試題. 2021年的中考試題中這樣的試題秉承了以往的特色，或以代數為主綜合考查數學概念、數學運算和建模能力;或以幾何為主綜合考查幾何直觀、空間觀念和推理能力. 在數學內部從“式”結構到“形”結構，從歸納到推理，從特殊到一般，突出考查分類與模型、數形結合等數學思想與創新意識.

（1）以代數知識為主考查數學概念、數學運算.

例1 （江蘇·南通卷）定義：若一個函數圖象上存在橫、縱坐標相等的點，則稱該點為這個函數圖象的“等值點”. 例如，點（1，1）是函數[y=12x+12]的圖象的“等值點”.

（1）分別判斷函數y = x + 2，y = x2 - x的圖象上是否存在“等值點”？如果存在，求出“等值點”的坐標;如果不存在，說明理由.

（2）設函數[y=3x]（x > 0），y = -x + b的圖象的“等值點”分別為點A，B，過點B作BC⊥Ox，垂足為點C. 當△ABC的面積為3時，求b的值.

（3）若函數y = x2 - 2（x ≥ m）的圖象記為W1，將其沿直線x = m翻折后的圖象記為W2. 當W1，W2兩部分組成的圖象上恰有2個“等值點”時，直接寫出m的取值范圍.

【評析】命題者從所熟悉的一次函數出發，關注到函數圖象上的特殊點“等值點”，并由具體的一次函數[y=12x+12]上的等值點聯想到其他函數是否存在這樣的等值點. 因此，所設計的問題涵蓋了一次函數、反比例函數和二次函數. 概念的理解是為了明確研究對象，在明確研究對象的基礎上，命題者從概念出發設置問題，考查學生對等值點的深度理解. 在第（2）小題中探究反比例函數和一次函數的等值點的關系. 在第（3）小題中研究二次函數的等值點的個數與函數圖象變化之間的關系，皆是對這一概念外延的相關知識的考查. 該題立意開闊，呈現簡潔，以一聯三，從特殊到一般，數形結合，自然而然.

（2）以幾何知識為主考查幾何直觀、空間觀念.

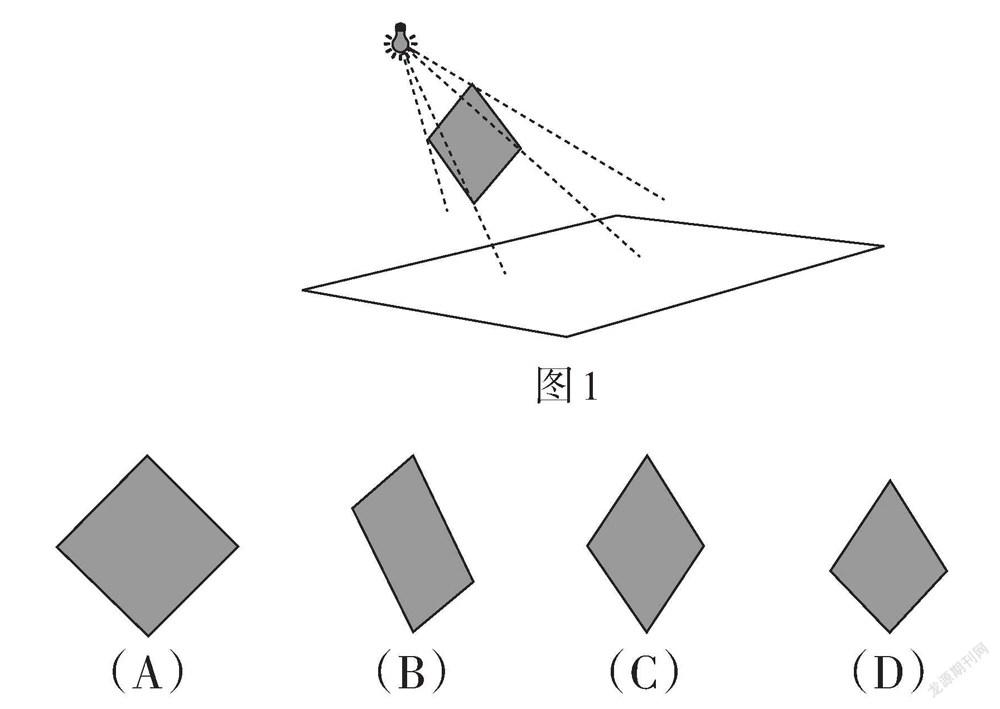
例2 （江蘇·南京卷）如圖1，正方形紙板的一條對角線垂直于地面，紙板上方的燈（看作一個點）與這條對角線所確定的平面垂直于紙板. 在燈光照射下，正方形紙板在地面上形成的影子的形狀可以是

（? ? ）.

【評析】此題綜合考查了特殊四邊形的性質、中心投影的相關知識，關注幾何直觀和空間觀念. 試題從“投影”中取材，結合四邊形的相關性質成題，背景熟悉而公平，豐富而簡潔. 試題四個選項的設計各有特色：A是基于原題中燈光照射對象本身的形狀而呈現;B是基于所給平面視角下的正方形紙板的形狀而呈現;C是基于正方形與菱形的關系，在“可能”處選擇菱形而呈現.

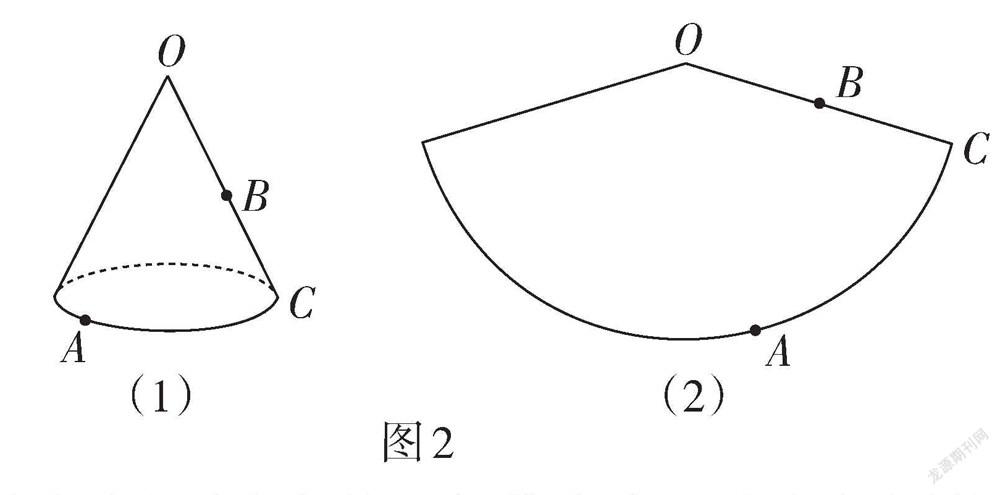
例3 （江蘇·南京卷）在幾何體表面上，螞蟻怎樣爬行路徑最短？

（1）如圖2（1），圓錐的母線長為12 cm，B為母線OC的中點，點A在底面圓周上，[AC]的長為4π cm. 在如圖2（2）所示的圓錐的側面展開圖中畫出螞蟻從點A爬行到點B的最短路徑，并標出它的長（結果保留根號）.

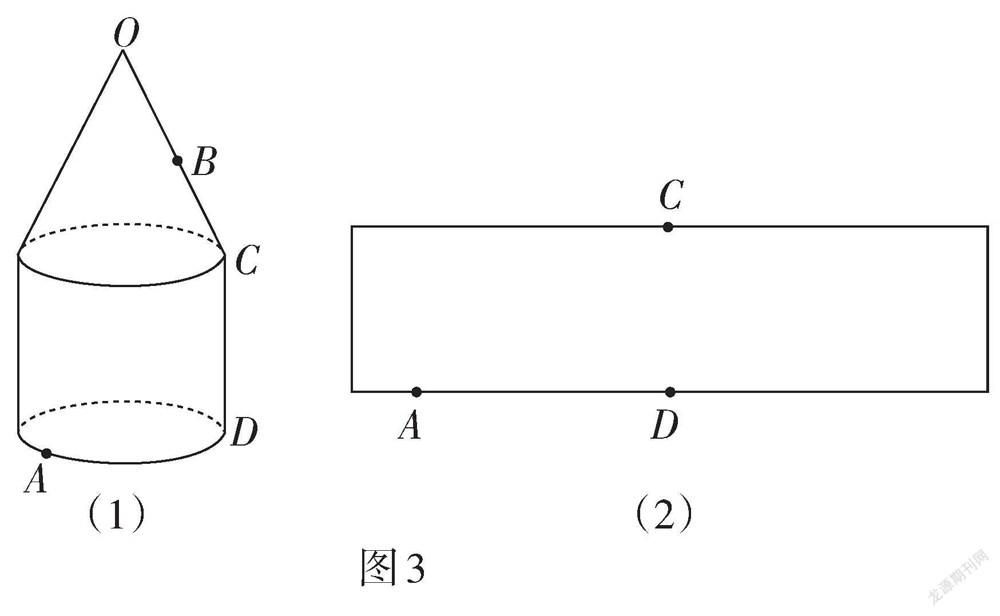
（2）圖3（1）中的幾何體由底面半徑相同的圓錐和圓柱組成. O是圓錐的頂點，點A在圓柱的底面圓周上. 設圓錐的母線長為l，圓柱的高為h.

① 螞蟻從點A爬行到點O的最短路徑的長為

（用含l，h的代數式表示）.

② 設[AD]的長為a，點B在母線OC上，OB = b. 圓柱的側面展開圖如圖3（2）所示，在圖中畫出螞蟻從點A爬行到點B的最短路徑的示意圖，并寫出求最短路徑的長的思路.

【評析】此題綜合考查了圓柱和圓錐的展開與折疊、勾股定理、相似三角形的判定與性質、三角函數和方程思想等相關知識. 關注直觀想象、數學建模、數學運算等素養，需要學生先通過想象大致感知最短的狀態. 其中，寫思路來描述思維過程的呈現方式獨具一格，目的是跳出機械的運算，重點關注思維的方向和路徑. 題目的三道小題之間有一定的層次性. 第（1）小題是圓錐上的最短路徑，第（2）小題是特殊化點B的位置. 這兩道小題都是第（3）小題的特殊情況. 而學生解答第（3）小題時有困難，但解題思路一脈相承，將立體圖形的“最短”轉化為平面圖形的“最短”，通過讓學生畫圖、寫思路，更好地保證試卷的信度和效度.

（3）綜合代數幾何考查分類討論、數形結合.

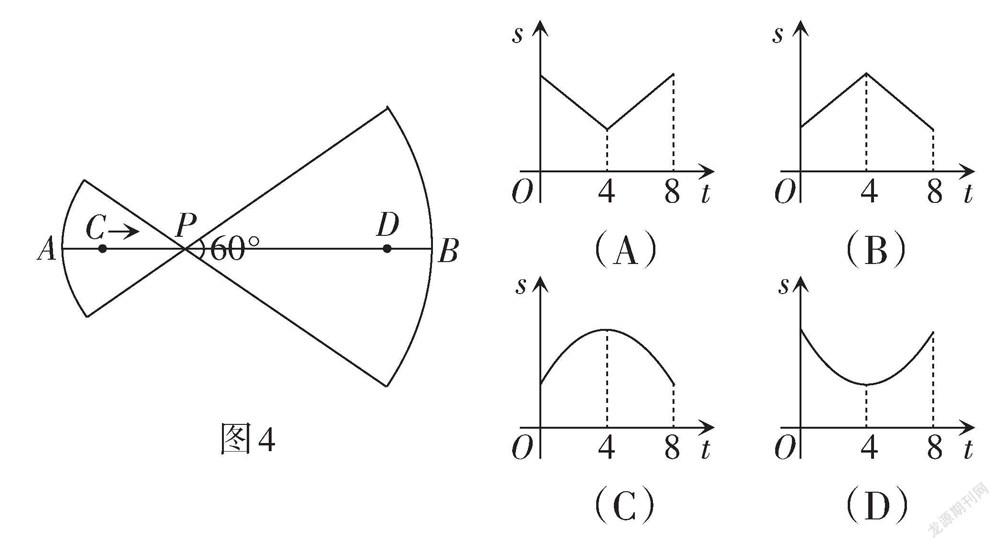
例4 （江蘇·蘇州卷）如圖4，線段AB = 10，點C，D在AB上，AC = BD = 1. 已知點P從點C出發，以每秒1個單位長度的速度沿著AB向點D移動，到達點D后停止移動. 在點P的移動過程中，做如下操作：先以點P為圓心，PA，PB的長為半徑分別作兩個圓心角均為60°的扇形，再將兩個扇形分別圍成兩個圓錐的側面，設點P的移動時間為t（單位：秒），兩個圓錐的底面面積之和為S，則S關于t的函數圖象大致是（ ? ）.

【評析】此題是動點圖象問題，綜合考查扇形、圓錐及函數的相關知識. 題目呈現輕巧，由點動到線動，由線動到形變，關注數形結合思想、函數模型思想. 在這一變化中，可研究的變量眾多，命題者則是選擇了圓錐的底面積之和與運動時間之間的關系進行研究. 一方面，是考查知識的覆蓋面所需;另一方面，也是由變量之間關系式的可表達而定.

例5 （江蘇·常州卷）【閱讀】

通過構造恰當的圖形，可以對線段長度、圖形面積大小等進行比較，直觀地得到一些不等關系或最值，這是數形結合思想的典型應用.

【理解】

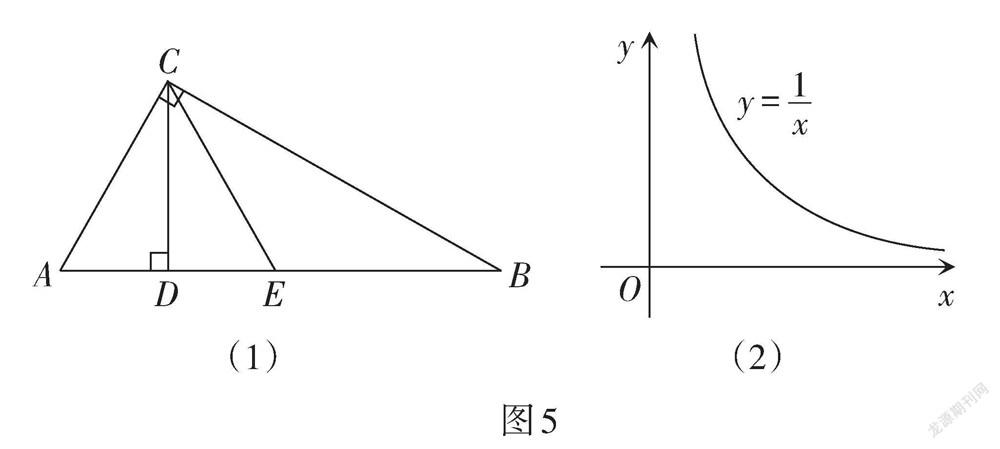
（1）如圖5（1），AC⊥BC，CD⊥AB，垂足分別為點C，D，E是AB的中點，連接CE. 已知AD = a，BD = b（0 < a < b）.

① 分別求線段CE，CD的長（用含a，b的代數式表示）;

②比較大小：CE? ? CD（填“<”“=”或“>”），并用含a，b的代數式表示該大小關系.

【應用】

（2）如圖5（2），在平面直角坐標系xOy中，點M，N在反比例函數[y=1x]（x > 0）的圖象上，橫坐標分別為m，n. 設p = m + n，[q=1m+1n]，記l =[14]pq.

① 當m = 1，n = 2時，l = ? ? ;當m = 3，n = 3時，l = ? ? .

② 通過歸納猜想，可得l的最小值是 ? ? . 試利用圖5（2）構造恰當的圖形，并說明你的猜想成立.

【評析】此題屬于反比例函數綜合題，綜合考查了反比例函數的性質、相似三角形的判定和性質、直角三角形斜邊中線的性質等知識. 命題者從“數缺形時少直觀，形缺數時難入微”進行立意，以閱讀理解的形式呈現問題，直指“數形結合”，從簡入繁，從三角形中特殊線段長度的研究到反比例函數k的幾何意義的理解，從歸納猜想到驗證說理，將以數定形、以形助數的價值凸顯出來，關注到直觀想象、邏輯推理等數學學科核心素養的考查.

2. 關注數學文化與知識結合的考查

在近年來的各地中考試題中，出現了一些數學文化融入評價中的導向，這一嘗試促使數學的學習更具開闊的視野，凸顯了數學文化的育人價值. 在具體的試題命制中呈現的特色主要體現在兩個方面：與數學趣味素材相結合、與數學史相結合. 這些試題對命題的要求極高，命題者既要關注到素材的公平性，保障試題的信度，又要關注到素材的取舍和處理，體現較好的效度. 因此，多數試題的嘗試還有待進一步研究和創新.

例6 （貴州·安順卷）（1）閱讀理解.

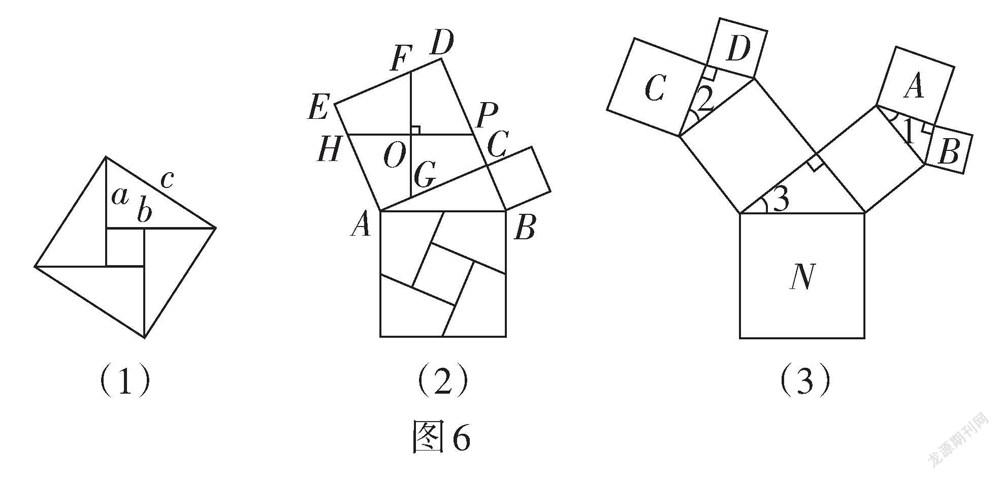
我國是最早了解勾股定理的國家之一，它被記載于我國古代的數學著作《周髀算經》中. 漢代數學家趙爽為了證明勾股定理，創制了一幅如圖6（1）所示的“弦圖”，后人稱之為“趙爽弦圖”.

根據“趙爽弦圖”寫出勾股定理和推理過程.

（2）問題解決.

勾股定理的證明方法有很多，圖6（2）是古代的一種證明方法：過正方形ACDE的中心O，作FG⊥HP，將它分成4份，所分成的四部分和以BC為邊的正方形恰好能拼成以AB為邊的正方形. 若AC = 12，BC = 5，求EF的值.

（3）拓展探究.

如圖6（3），以正方形一邊為斜邊向外作直角三角形，再以該直角三角形的兩直角邊分別向外作正方形，重復這一過程就可以得到“勾股樹”的部分圖形. 設大正方形N的邊長為定值n，小正方形A，B，C，D的邊長分別為a，b，c，d.

已知∠1 = ∠2 = ∠3 = α，當角α（0° < α < 90°）變化時，探究b與c的關系式，并寫出該關系式及解答過程（b與c的關系式用含n的式子表示）.

【評析】此題從“趙爽弦圖”出發，綜合考查了正方形的性質、全等三角形的性質、勾股定理的證明、相似三角形的判定與性質等知識. 需要學生先明白根據“趙爽弦圖”推理勾股定理的方法，再以此為基礎進行拓展探究. 這里的拓展探究體現命題者對“勾股樹”特征研究的獨特見解，將相似三角形的知識藏于其中，引導學生發現c + b = n這樣的規律，彰顯了數學文化的影響力. 此題關注了對學生幾何直觀、空間觀念和邏輯推理能力的考查.

3. 關注數學思維與實驗融合的考查

基于數學實驗進行評價一直是“綜合與實踐”考查的主要方式. 試題呈現往往需要學生經歷觀察、操作、探索、驗證、反思來體現數學思考的過程. 既注重外顯的操作表達，更注重頭腦中的內隱認知、思想領悟和意義建構. 這些試題的特征大體以幾何素材為背景，需要學生運用直觀感知、操作確認、推理論證、度量計算等認識圖形，并探索圖形的性質，確定圖形的形狀、大小和位置關系. 常常以剪拼、折疊及旋轉等變化方式呈現.

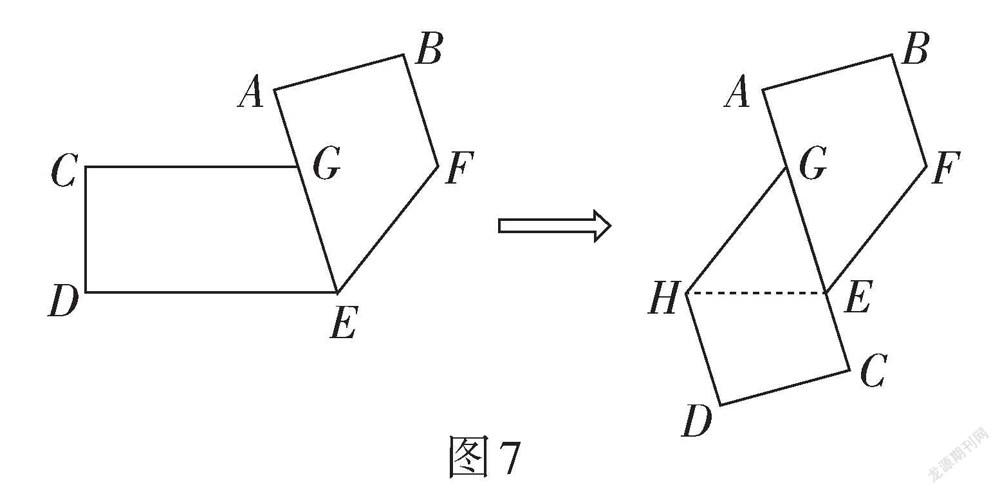
例7 （山東·威海卷）如圖7，先將矩形紙片ABCD沿EF折疊（邊AB與DE在CF的異側），AE交CF于點G;再將紙片折疊，使CG與AE在同一條直線上，折痕為GH. 若∠AEF = α，紙片寬AB = 2 cm，則HE = ? ? ? ? .

【評析】此題是常見的折紙問題，綜合考查了軸對稱的性質、平行四邊形的判定與性質、矩形的性質、銳角三角函數，需要學生在感知圖形變化中確定研究對象. 命題者將折疊的紙片從一次折疊突破到二次折疊，是折紙問題的延伸. 兩次折疊后的要求是“使CG與AE在同一條直線上”，這里給予了問題建構的空間. 命題者在這一特定要求下賦予角度和線段長度，引出關于HE長度與∠AEF角度關系的思考. 這里采用α表示，并沒有給出具體度數，避免特殊角度影響試題的效度，更體現了這個角度與HE長度的一般關系. 此題關注了幾何直觀、空間觀念和邏輯推理能力的考查.

例8 （黑龍江·齊齊哈爾卷）數學實踐活動是一種非常有效的學習方式，通過活動可以激發我們的學習興趣，提高動手、動腦能力，拓展思維空間，豐富數學體驗，讓我們一起動手來折一折、轉一轉、剪一剪，體會活動帶給我們的樂趣.

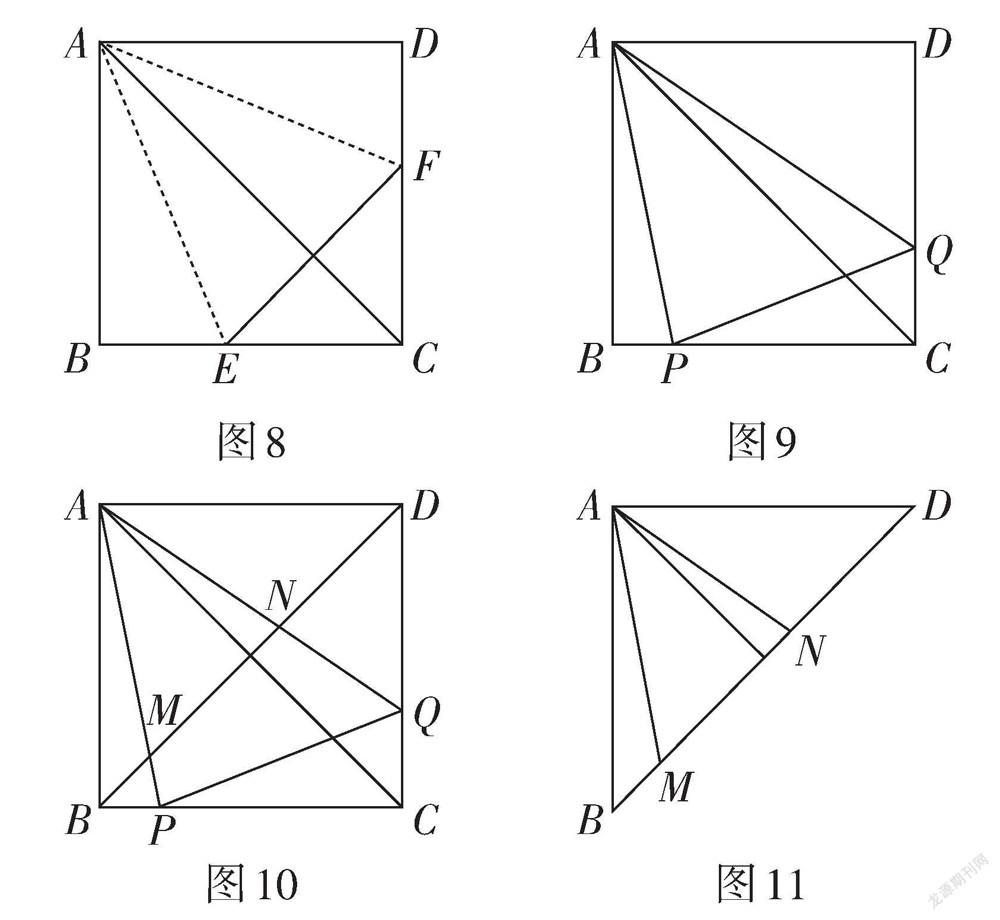
折一折：將正方形紙片ABCD折疊，使邊AB，AD都落在對角線AC上，展開得折痕AE，AF，連接EF，如圖8所示.

（1）∠EAF = ? ? ? ，寫出圖中兩個等腰三角形 ? ? （不需要添加字母）.

轉一轉：將圖8中的∠EAF繞點A旋轉，使它的兩邊分別交邊BC，CD于點P，Q，連接PQ，如圖9所示.

（2）線段BP，PQ，DQ之間的數量關系為? ? .

（3）連接正方形對角線BD，若圖9中的∠PAQ的邊AP，AQ分別交對角線BD于點M，N，如圖10所示，則[CQBM]= ? ? .

剪一剪：將圖10中的正方形紙片沿對角線BD剪開，如圖11所示.

（4）求證：BM2 + DN2 = MN2.

【評析】此題從“折一折、轉一轉、剪一剪”的角度綜合考查了正方形的性質、全等三角形的判定和性質、勾股定理、相似三角形的判定和性質等知識，需要學生在各種實驗操作的基礎上經歷觀察、想象、操作與思考. 此題從折紙開始，關注到對折到正方形紙片對角線處所形成的角和圖形的形狀的特殊性. 這一步引入是學生比較熟悉而且容易理解的操作，學生可以借助手中的素材直接操作驗證得到. 在“折一折”之后，命題者從運動的角度切入，以折得的角為研究對象，進行“轉一轉”，引發線段之間關系的探究. 兩道小題，一道小題考查全等三角形，一道小題考查相似三角形，相得益彰.“剪一剪”跳出了正方形框架，以獨特的視角看圖形變化. 一方面，是常見數學實驗操作的必然呈現，從折、轉到剪，豐富了實驗操作的內容;另一方面，是圖形生長的自然趨勢，從圖8到圖9是由特殊到一般，由定到變;從圖9到圖10是基于圖形元素之間的關聯，逐步“枝繁葉茂”;從圖10到圖11則是分解重組，推陳出新，構建新的圖形結構. 此題的整體立意巧妙，內部關聯緊密，關注了對學生幾何直觀、空間觀念、邏輯推理等能力的考查，滲透數形結合、特殊到一般的數學思想，體現“做中學”這一綜合與實踐開展的價值.

4. 關注數學與其他學科聯系的考查

跨學科主題是培養學生的創新意識、合作精神、實踐能力和社會責任感的一種綜合性探究學習方式. 近年來，從《標準》修訂到教材修改，從教學到評價，都在關注數學與其他學科之間的聯系. 評價什么、如何評價及學科聯系之間的程度如何確定等問題成為了評價嘗試的重點和創新點. 因此，需要命題者從學科整合的情境出發設計合理的問題，考查學生綜合運用數學學科和跨學科的知識與方法來解決問題的能力. 當前跨學科的評價試題還不夠多，內容涉及其他學科還不夠豐富，常與物理、化學、生物、體育、信息等學科進行聯系，與其他學科乃至多個學科關聯的綜合型問題有待開發.

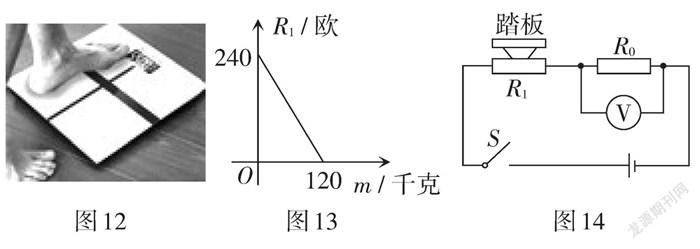
例9 （浙江·臺州卷）如圖12所示的電子體重秤讀數直觀又便于攜帶，為人們帶來了方便. 某綜合實踐活動小組設計了簡易電子體重秤：制作一個裝有踏板（踏板質量忽略不計）的可變電阻R1，R1與踏板上人的質量m之間的函數關系式為R1 = km + b（其中k，b為常數，0 ≤ m ≤ 120），其圖象如圖13所示;圖14的電路中，電源電壓恒為8伏，定值電阻R0的阻值為30歐，接通開關，人站上踏板，電壓表顯示的讀數為U0，該讀數可以換算為人的質量m.

溫馨提示：① 導體兩端的電壓U，導體的電阻R，通過導體的電流I，滿足關系式I =[UR];

② 串聯電路中電流處處相等，各電阻兩端的電壓之和等于總電壓.

（1）求k，b的值;

（2）求R1關于U0的函數解析式;

（3）用含U0的代數式表示m;

（4）若電壓表量程為0 ～ 6伏，為保護電壓表，試確定該電子體重秤可稱的最大質量.

【評析】此題以物理中的電路問題為背景，綜合考查了一次函數、反比例函數等相關知識，關注到數形結合思想，體現了對數學運算、數學建模能力的考查. 試題需要學生在理解物理知識的基礎上，確定函數關系式. 第（4）小題可以應用反比例函數的增、減性，也可以將m與U0的關系式轉化為關于m的不等式，再代入0 ≤ U0 ≤ 6中，求出電子體重秤可稱的最大質量m. 此題與物理學科知識緊密聯系，其中“溫馨提示”具有人文性，也避免了學生對個別物理知識的理解不同對數學綜合應用考查的效度影響.

5. 關注數學與社會生活聯系的考查

數學知識與現實世界是緊密聯系的，在現實世界中用數學眼光觀察問題，用數學思維思考問題和解決問題是數學學科的素養體現，是認識、理解、表達現實世界的工具、方法和語言. 因此，結合數學課程內容和問題解決的真實需要，設計恰當的綜合主題和探究任務進行評價，考查學生親歷實踐、探究、體驗、反思、合作、交流等學習過程所獲取的數學經驗是各地中考長久以來的評價重點. 多年來，創設問題情境體現應用意識的試題層出不窮，涵蓋了我們生活的方方面面，但設計的評價試題如何能考查學生綜合運用數學知識與方法解決現實世界的數學問題一直是所有人追求的方向.

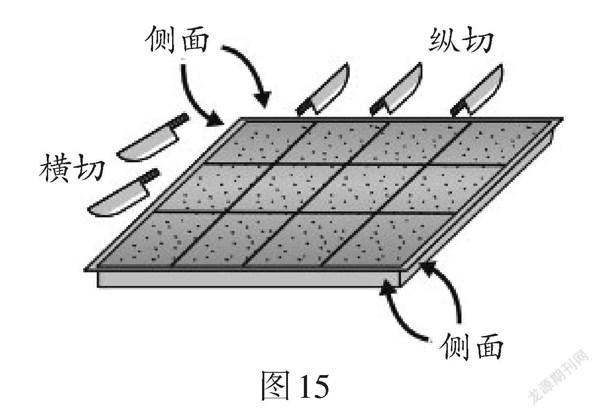
例10 （臺灣卷）凱特平時常用底面為矩形的模具制作蛋糕，并以平行于模具任一邊的方式進行橫切或縱切，橫切都是從模具的左邊切割到模具的右邊，縱切都是從模具的上邊切割到模具的下邊. 用這種方式，可以切出數個大小完全相同的小塊蛋糕. 在切割后，他發現小塊蛋糕接觸模具的地方外皮比較焦脆.? 以圖15為例，橫切2刀，縱切3刀，共計5刀，切出（2 + 1） × （3 + 1） = 12個小塊蛋糕，其中側面有焦脆的小塊蛋糕共有10個，所有側面都不焦脆的小塊蛋糕共有2個.

試根據上述切割方式，回答下列問題，并詳細解釋或完整寫出你的解題過程.

（1）若對一塊蛋糕切了4刀，則可切出幾個小塊蛋糕？試寫出任意一種可能的蛋糕塊數即可.

（2）今凱特根據一場聚餐的需求，打算制作出恰好60個所有側面都不焦脆的小塊蛋糕，為了避免勞累并加快出餐速度，在不超過20刀的情況下，試問凱特需要切幾刀，才可以達到需求？寫出所有可能的情形.

【評析】此題以“制作蛋糕”的實際生活背景為素材，綜合考查規律探究、方案設計等知識，需要學生積累生活經驗，將實際問題數學化，滲透了對幾何直觀、數形結合和分類討論思想的綜合考查. 試題素材貼近學生，問題的呈現由易到難，凸顯真實性.

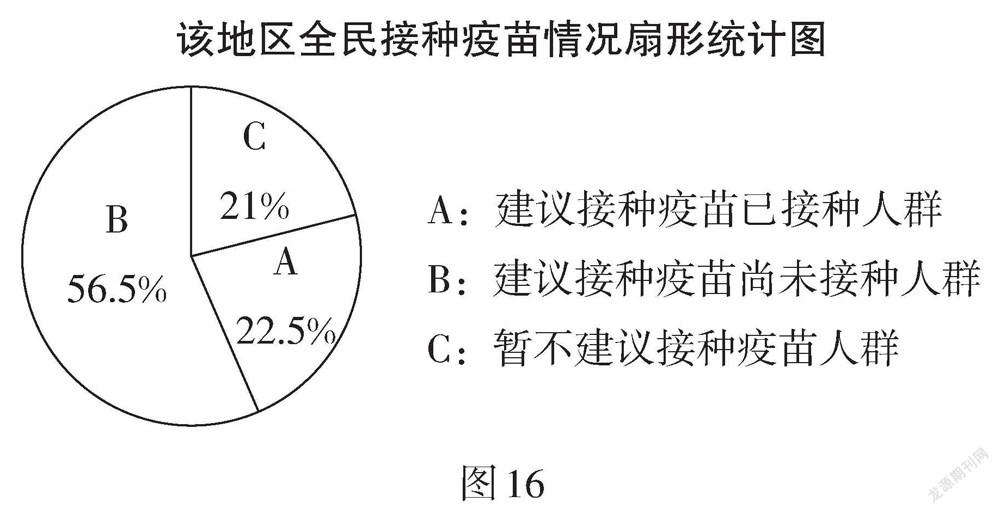
例11 （江蘇·鹽城卷）為了防控新冠肺炎疫情，某地區積極推廣疫苗接種工作，衛生防疫部門對該地區八周以來的相關數據進行收集整理，繪制得到對應圖表如圖16、表1所示.

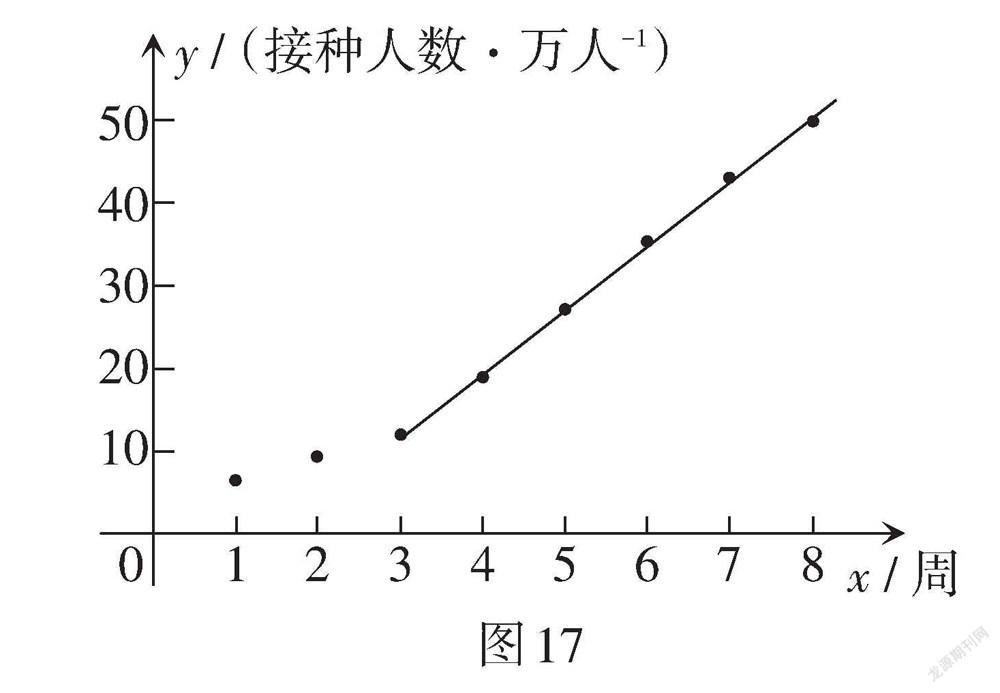
根據統計表1中的數據，建立以周次為橫坐標，接種人數為縱坐標的平面直角坐標系，并根據以上統計表中的數據描出對應的點，發現從第3周開始這些點大致分布在一條直線附近，現過其中兩點（3，12），（8，42）作一條直線（如圖17，該直線的函數表達式為y = 6x - 6），那么這條直線可近似反映該地區接種人數的變化趨勢.

試根據以上信息，解答下列問題：

（1）這八周中每周接種人數的平均數為 ? ? ? ;該地區的總人口約為 ? ? ? .

（2）若從第9周開始，每周的接種人數仍符合上述變化趨勢.

① 估計第9周的接種人數約為 ? ? ? ;

② 專家表示：疫苗接種率至少達60%才能實現全民免疫. 那么，從推廣疫苗接種工作開始，最早到第幾周，該地區可達到實現全民免疫的標準？

（3）實際上，受疫苗供應等客觀因素影響，從第9周開始接種人數將會逐周減少a（a > 0）萬人，為了盡快提高接種率，一旦周接種人數低于20萬人時，衛生防疫部門將會采取措施，使得之后每周的接種能力一直維持在20萬人. 如果a = 1.8，那么該地區的建議接種人群最早將于第幾周全部完成接種？

【評析】此題關注社會熱點問題，以防控新冠肺炎疫情推廣疫苗接種為背景取材，立意積極向上，數據科學真實. 綜合考查了一次函數的應用、平均數、不等式等相關知識. 對平均數的考查需要學生理解并提取表格信息，關注學生信息提取能力的考查;第（2）小題的設計則是基于已有的表格信息，結合擬合的一次函數考查一次函數的應用，體現以數據說話進行“估計”的價值;第（3）小題則是進一步在一次函數理解的基礎上融入不等式，考查不等式模型的建立. 命題者將這些素材的數學立意圍繞“疫苗接種”進行設計，既有梯度，又有效度，考查了學生解決實際問題的能力，體現了對“會用數學眼光觀察世界，會用數學思維思考世界，會用數學語言表達世界”的數學學科核心素養的評價.

三、復習建議

綜合與實踐是幫助學生積累數學活動經驗、培養應用意識和創新意識、提升數學學科核心素養的重要和有效載體. 多年來，一直是全國中考試題關注的重點，更是落實立德樹人、進行學科育人評價的難點. 各區域的命題在不斷改革和創新，呈現出更具綜合性、真實性、科學性和時代性的特征. 綜合與實踐的試題主要評價學生在理解數學知識結構的基礎上，重新建構數學認知的完善程度、方法路徑以及經驗獲取的轉化、遷移能力;考查學生通過運算、推理進行歸納、演繹得到新的結論，解決與其他學科、與生活緊密聯系的問題;引導學生在學習和評價中體會數學知識的價值，以及與其他學科知識的關聯. 基于此，針對2022年中考，關于綜合與實踐的復習提出以下幾點建議.

1. 整體把握課程目標，系統復習綜合實踐

為了使每名學生都受到良好的數學教育，數學教學不僅要使學生獲得數學知識技能，而且要把“知識技能”“數學思考”“問題解決”“情感態度”四個方面有機結合，整體實現課程目標. 因此，綜合與實踐能力的提升不在于做多少試題，而在于解決問題的能力，需要細化分解，有針對性地進行專題復習，夯實基礎運算、基本技能. 例如，針對函數綜合試題，可以選擇一個有效的載體串起多類型函數知識，將函數圖象與性質進行關聯;在綜合復習中可以嘗試以“模塊化”進行設計. 例如，圍繞“垂直”串起初中所有與這一特殊位置關系有關聯的知識;在綜合與實踐中常見的分類思想、模型思想和數形結合思想可以選擇方案設計、圖形變化、問題解決等類型試題進行鞏固……所以，教師要重視對教學內容的整體分析，了解數學知識的產生與來源、結構與關聯、價值與意義，并以此進行中考復習. 因此，中考復習需要系統設計，從整體課程目標出發，合理安排時間，科學選擇專題.

2. 深挖數學文本資源，拓寬學生數學視野

理解數學從理解《標準》、深讀教材文本開始. 一線數學教師有必要深度理解數學教材的編寫意圖，關注數學文本中豐富的資源. 在教材中，綜合與實踐的內容多數是融入課時學習中進行的，也有一部分是以課題學習、數學活動、數學實驗室等形式突出體現. 在平時教學和中考復習中要將這些綜合與實踐的素材理解到位，分析各地區綜合與實踐的試題與文本資源的關聯程度，選擇有效的同類型載體，進一步挖掘文本資源可拓展的空間. 例如，探尋勾股數組中所體現出來的代數推理的價值，折紙活動中所體現出來的幾何直觀和邏輯推理能力，等等. 在深挖文本資源的同時，建議適當拓寬學生的數學視野，選擇貼近學生生活的素材培養其數學的眼光，有利于他們經歷從現實情境中抽象出數學知識與方法. 所選擇的素材要關注到生活現實、數學現實和其他學科現實. 這些素材應考慮到學生的最近發展區，應揭示學科知識的內在聯系，體現數學學科的整體性;應盡量選擇來源于生活、社會中的現象和問題，體現數學學科的應用性;應巧妙地與其他學科之間建立聯系，體現數學學科的基礎性. 具體呈現方式則在符合學生認知需求的同時，更有助于學生理解數學的本質，引發學生深入思考，以使學生感受到數學的趣味、價值和意義.

3. 創新數學教學方式，重視學生主體地位

數學知識的形成及逐漸完善的過程中往往蘊含著一定的數學思想. 好的教學方式有利于促進學生自主探索，引發學生認知沖突，激發學生學習動機. 在綜合與實踐的復習教學中，不宜文本化教學，不宜題海式解題、講題. 需要引發學生積極的數學思考，讓學生在問題解決中體驗成功的快樂. 例如，組織可操作的折紙實驗、測量活動、閱讀欣賞等形式促進學生共同進行設疑、質疑、釋疑的數學活動，幫助學生養成良好的學習習慣，促進學生學會學習.

多年來，綜合與實踐的評價如何更好地落實立德樹人、學科育人的任務是所有命題者的不懈追求. 正確看待評價的測量功能，認識到評價的價值導向才能更有利于一線教學關注學生的數學理性精神的培育，促進學生數學學科核心素養的發展.

四、模擬題欣賞

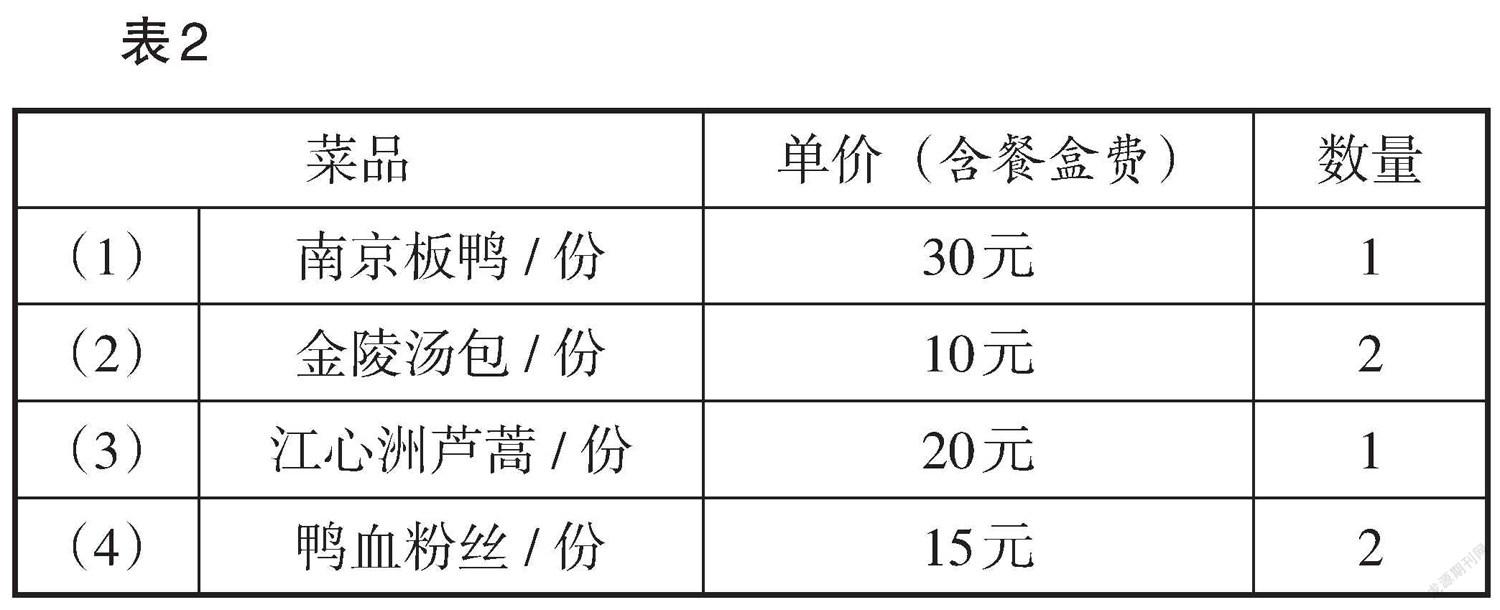
1. 小寧計劃在某外賣網站下單購買如表2所示的菜品. 已知每份訂單的配送費為3元，商家為了促銷，對每份訂單的總價（不含配送費）提供滿減優惠：滿30元減15元，滿60元減35元，滿80元減40元，滿100元減45元. 如果小寧在購買表2中的任意三項菜品時，采取適當的下訂單方式，那么他點餐的總費用優惠幅度最大可為? ? ? ? ?.

答案：44元.

2.【學習理解】

定義：平面上與已知線段兩個端點連接而形成直角三角形的點我們稱為已知線段的“勾股點”. 若一個點是兩條已知線段的“勾股點”，則該點為這兩條線段的“公共勾股點”.

【概念鞏固】

（1）如圖18，已知在Rt△ABC中，AC = 3，BC = 4，∠C = 90°. 試借助尺規在邊BC所在直線上確定點P，使得點P為AB的“勾股點”，并求PC的長.

（2）若點P為（1）中Rt△ABC兩邊AB，BC的公共“勾股點”，則PC的最大值為 ? ? ?.

【深入研究】

（3）如圖19，已知△ABC，P為AB和BC的公共“勾股點”. 連接PB交AC于點Q，若點Q恰好是AB和BC的另一個公共“勾股點”. 求證：△ABC為等腰三角形.

【直觀猜想】

（4）是否存在一個點P和△ABC，使得P為△ABC三邊的公共“勾股點”. 如果存在，畫出示意圖;如果不存在，說明理由.

答案：（1）如圖20所示;PC =[94].

（2） 5.

（3）證明略.

（4）存在，如直角三角形（如圖21）.

3. 定義：一般地，對兩個封閉圖形甲、乙，若甲的頂點都在乙的邊界上，則稱甲是乙的內接圖形，乙是甲的外接圖形（圖形甲的邊可以和圖形乙的邊重合）.

已知，在△ABC中，∠ACB = 90°，AC = 2，BC = 3. 如圖22，矩形DEFG是△ABC的外接矩形，正方形BCHI是△ABC的外接正方形，等邊三角形JKL是△ABC的外接等邊三角形.

顯然，一個圖形的外接多邊形不唯一，我們可以探索△ABC的最小外接多邊形.

（1）試在圖23中分別畫出△ABC的最小外接矩形、最小外接正方形、最小外接等邊三角形的示意圖，并直接寫出它們的邊長.

（2）類似地，用一張等邊三角形紙片剪一個直角邊長分別為1 cm和3 cm的直角三角形紙片，等邊三角形紙片的邊長最小是多少？畫出示意圖，并寫出這個最小值.

答案：（1）① 如圖24（1），矩形ACBE是△ABC的最小外接矩形，AC = 2，BC = 3;

② 如圖24（2），正方形MNBQ是△ABC的最小外接正方形，邊長為[91010];

③ 如圖24（3），等邊三角形ABP是△ABC的最小外接等邊三角形，邊長為[13].

（2）如圖25，等邊三角形AMN即為所求，邊長為[3010+91010]cm.

參考文獻：

[1]中華人民共和國教育部制定. 義務教育數學課程標準（2011年版）[M]. 北京：北京師范大學出版社，2012.

[2]教育部基礎教育課程教材專家工作委員會. 《義務教育數學課程標準（2011年版）》解讀[M]. 北京：北京師范大學出版社，2012.