以變式教學育核心素養

林鴻德

摘? 要：在復習課教學中，以變式教學研析“銳角三角函數及其應用”，對于數學學科核心素養的培養有著很強的專業性和針對性，能有效引導學生多角度、多方位思考問題，通過總結反思，提煉解決問題的通性、通法，揭示數學問題的本質，發展學生的數學建模和邏輯推理素養，拓展學生的思維，有利于學生的思維品質和關鍵能力的形成和發展，有效提高學生的數學學科核心素養.

關鍵詞：變式教學;核心素養;思維品質

數學學科核心素養是以數學課程教學為載體，基于數學學科的知識技能而形成的重要的思維品質和關鍵能力.《普通高中數學課程標準（2017年版）》（以下簡稱《標準（2017年版）》）首次提出數學學科六大核心素養，分別為數學抽象、邏輯推理、數學建模、直觀想象、數學運算和數據分析.《義務教育數學課程標準（2011年版）》（以下簡稱《標準（2011年版）》）明確提出要重視十個核心關鍵詞，分別為數感、符號意識、空間觀念、幾何直觀、數據分析觀念、運算能力、推理能力、模型思想、應用意識和創新意識. 可以看出，《標準（2017年版）》的核心素養與《標準（2011年版）》中提出的核心關鍵詞是一脈相承的，關鍵要素的表達是基本一致的. 因此，培養數學學科核心素養是新時代對教師的要求.

變式教學是對學生進行數學技能和思維訓練的重要方式，是培養學生數學學科核心素養的重要平臺. 通過變式教學引導學生多角度、多方位思考問題，讓學生從“變”的現象中發現“不變”的本質，從“不變”的本質中探索“變”的規律，優化學生的思維品質，有效提升學生的數學學科核心素養. 本文以復習課“銳角三角函數及其應用”的四個教學片斷為例，闡述以變式探究培育學生數學學科核心素養的認識與思考.

一、復習目標

“銳角三角函數及其應用”復習目標設置如下.

（1）能利用銳角三角函數、勾股定理、角角關系等知識解決直角三角形中的有關問題;會將斜三角形有關問題轉化為直角三角形問題來求解;應用銳角三角函數知識解決相關實際問題.

（2）通過變式探究的過程，感受知識之間的聯系，體驗解決問題的方法，滲透轉化與化歸、分類討論等數學思想，提高學生分析問題、解決問題的能力，優化數學思維品質，提升數學學科核心素養.

二、教學片斷

片斷1：探究邊角關系.

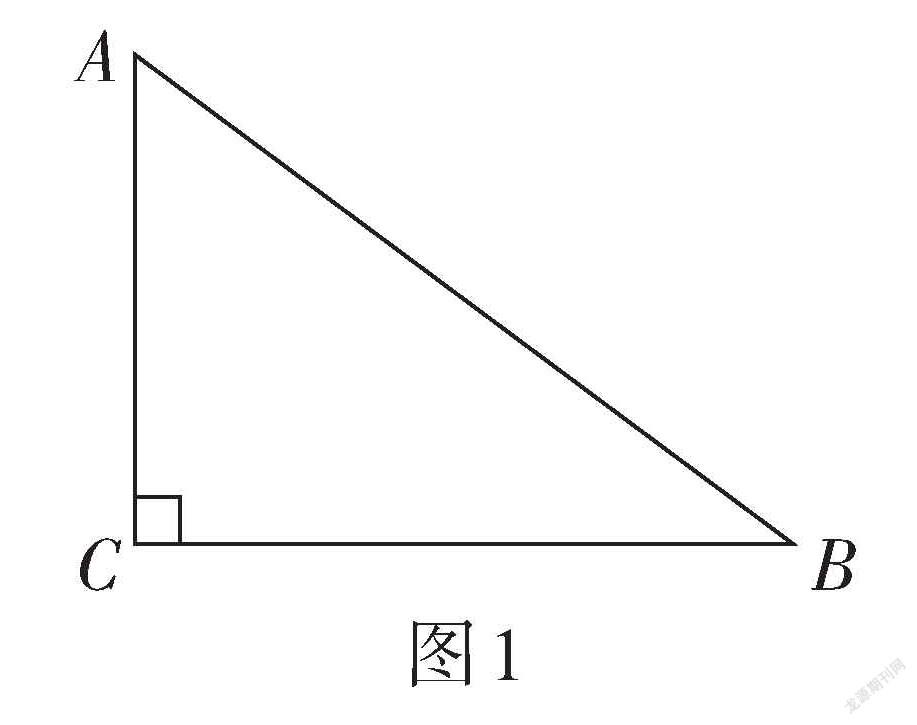
例1? 如圖1，在[Rt△ABC]中，[∠C=90°].

（1）若[AB=10，] [sinA=45，] 則[BC=_______;] [AC=][________;] [tanA=_________;] [cosA=_________.]

（2）若[AC=6，] [cosA=35，] 則[AB=_______;] [BC=][________;] [sinA=________;] [tanA=________.]

（3）若[AC=6，] [sinA=45，] 則[AB=______;] [BC=][________;] [cosA=________;] [tanA=________.]

（4）若[AC=3，] [AB=6，] 則[BC=_________;∠A=][________;] [∠B=________.]

【設計意圖】第（1） ～ （3）小題是已知一邊一角（三角函數），可利用邊角關系或勾股定理求其余的邊和角. 這三道小題剛好是三個不同類型，只要找準關系即可快速解題. 第（4）小題是已知兩邊，可利用勾股定理求第三邊，進而利用三角形的邊角關系求出對應的角. 此題通過一個圖形，把本節課的基礎知識串聯起來，以題點知，既讓學生回顧所學知識，又幫助學生形成良好的認知結構.

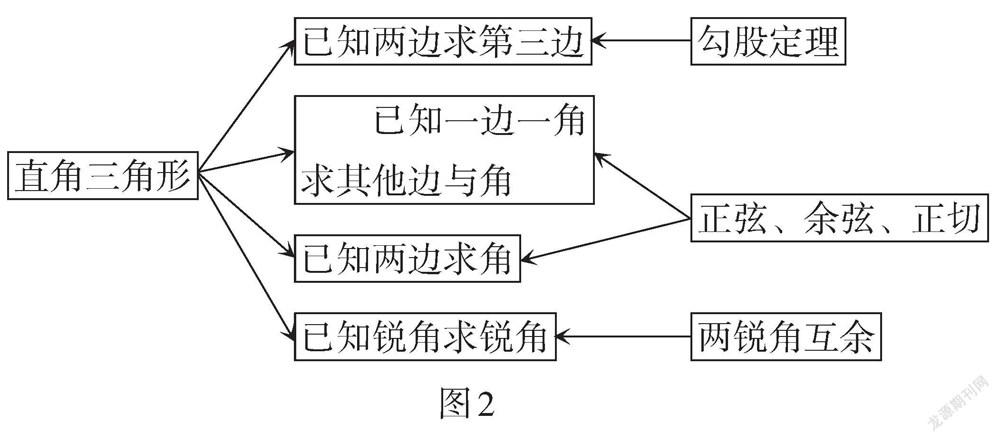
教師引導：通過以上變式，引導學生思考并領悟解決問題的策略. 在教師的引導下，形成以下知識結構，如圖2所示.

片斷2：探究三角函數值的求解.

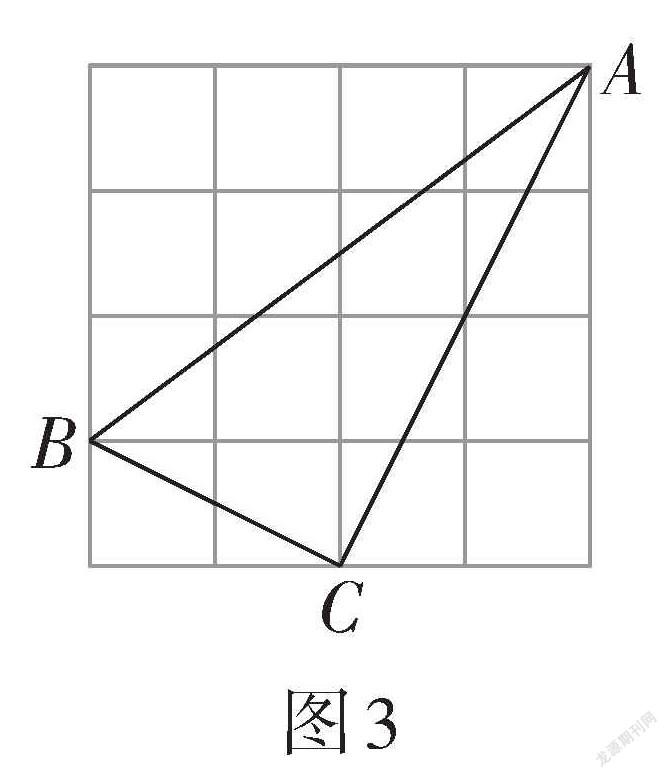
例2? 如圖3，△ABC的頂點都在格點上，則[tan∠BAC=]___________.

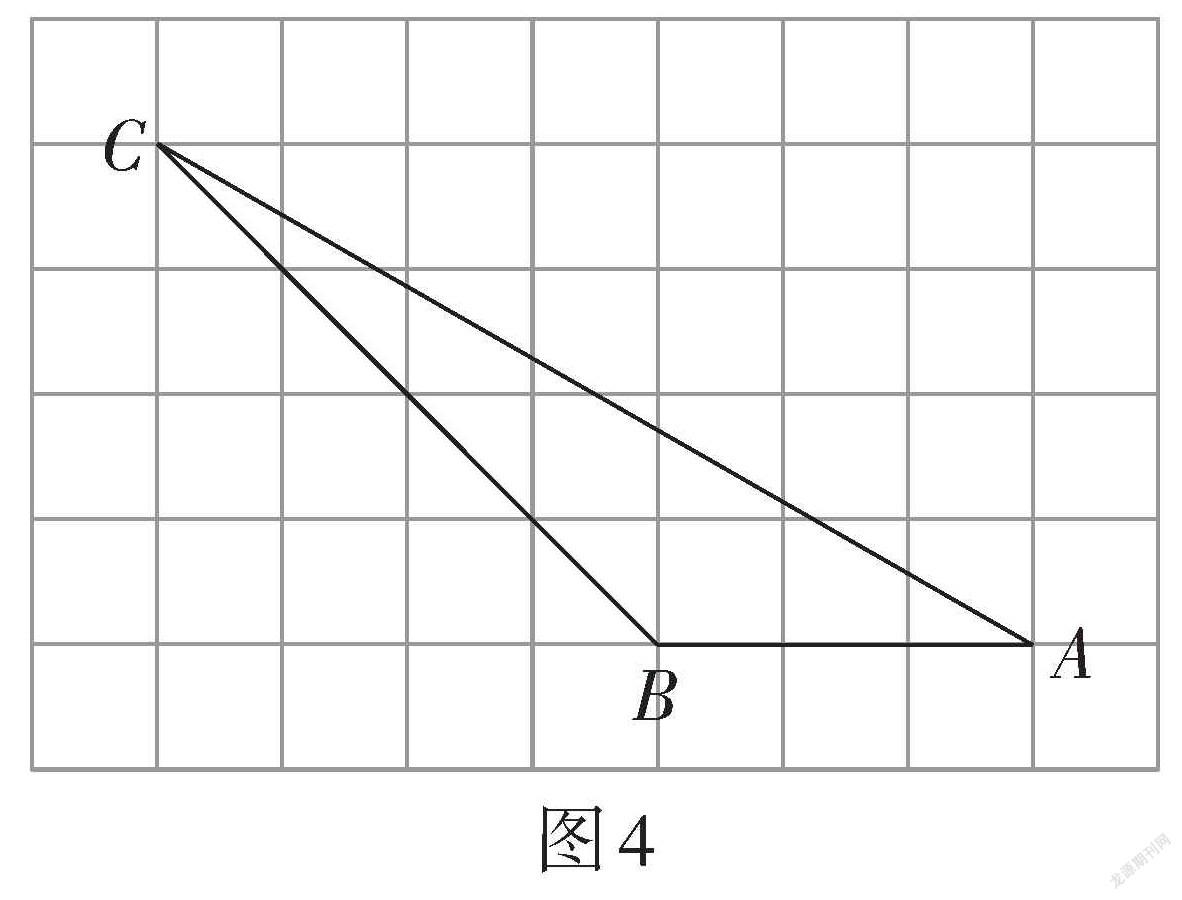
變式1：如圖4，△ABC的頂點都在格點上，則[tan∠BAC=]___________.

變式2：如圖5，△ABC中只有點A和點B在格點上，則[tan∠BAC=]___________.

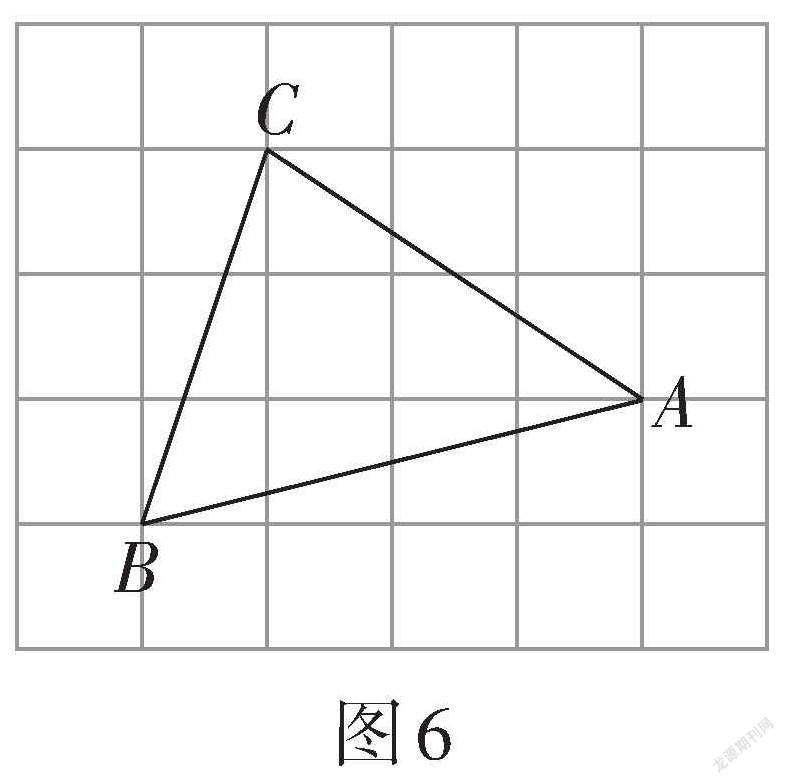
變式3：如圖6，△ABC的頂點都在格點上，則[tan∠BAC=]___________.

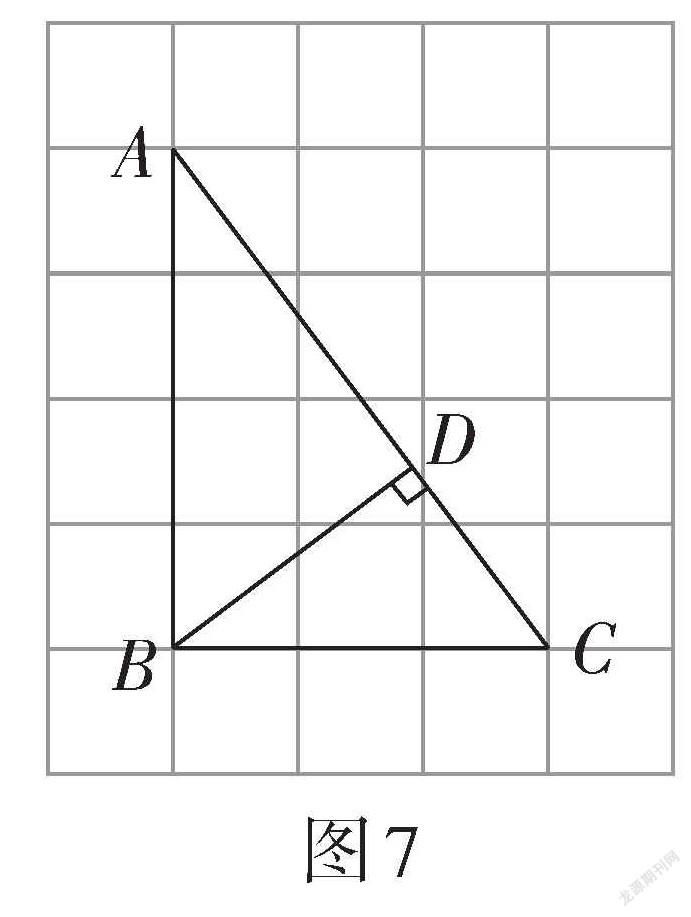
變式4：如圖7，△ABC的頂點都在格點上，則[tan∠BCD=]___________.

【設計意圖】例2的求解要先通過勾股定理的逆定理證明△ABC是直角三角形，進而求出三角函數值. 變式1 ～ 變式3都是給出斜三角形，學生需要構造直角三角形，才能利用邊角關系求出相應值. 不同點是變式1三個頂點都在格點上，直接過點C構造直角三角形. 而變式2只有兩個頂點在格點上，需要在直線AC上尋找落在網格點上的點才能構造出便于求解的直角三角形. 這兩個變式都有一條邊在網格線上，學生構造直角三角形后能快速得到相應邊的長. 變式3所有的邊都不在網格線上，學生在構造直角三角形時需要作出三角形的高，利用面積法求高，進而求出三角函數值. 對于變式4，學生容易重復變式3的解法進行求解，而實際上利用轉化思想，將所求角進行等角轉化，再求三角函數值，極大地優化了解題過程. 通過一題多變，引導學生多角度、多渠道思考問題，激發學生的學習興趣，培養學生的邏輯思維能力.

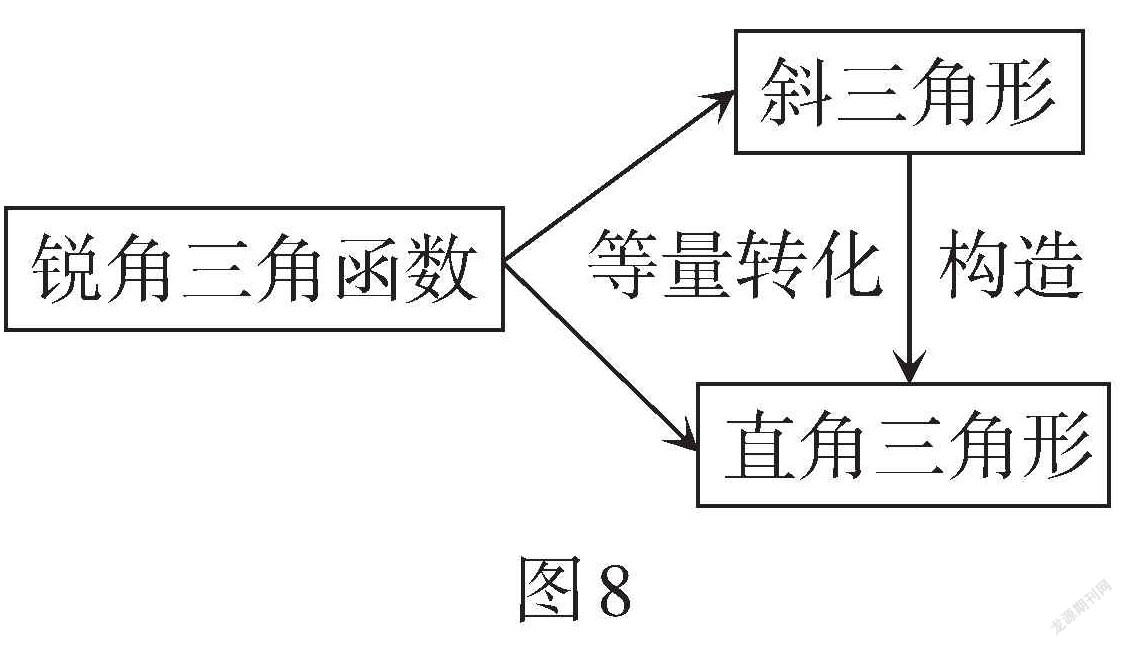
教師引導：通過以上變式，可以引導學生形成以下解決問題的策略（如圖8）. 如果所求的角在直角三角形內，可以直接利用三角函數的定義求出三角函數值. 如果所求的角在斜三角形中，可以直接構造直角三角形或等量轉化為直角三角形中的角. 另外，部分所求角雖然已在直角三角形中，有時為了簡化計算，也可以將其轉化到另一直角三角形進行求解.

片斷3：探究三角形面積.

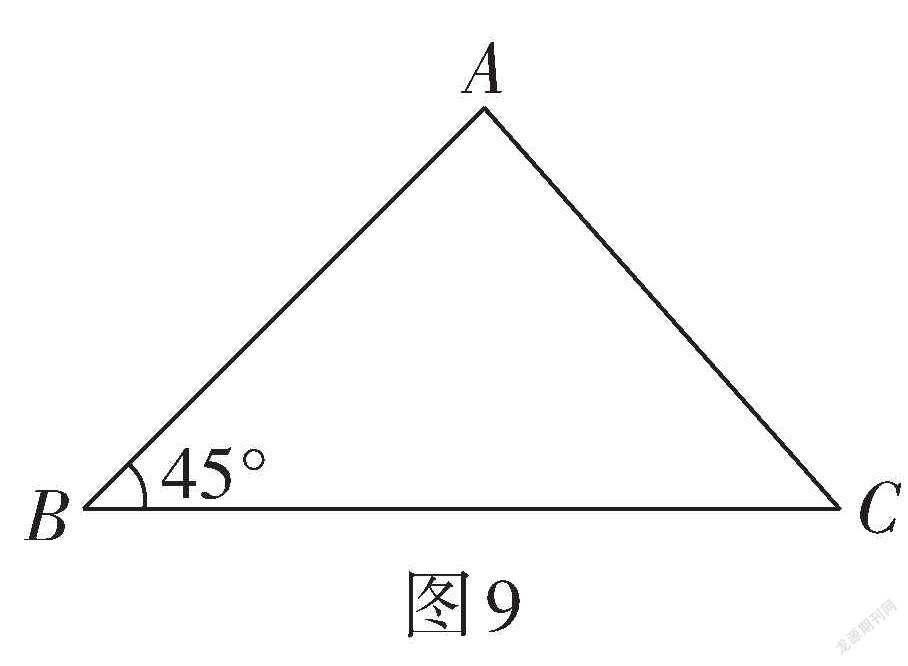
例3? 如圖9，在△ABC中，[AB=6，BC=8，∠B=][45°]，求[S△ABC].

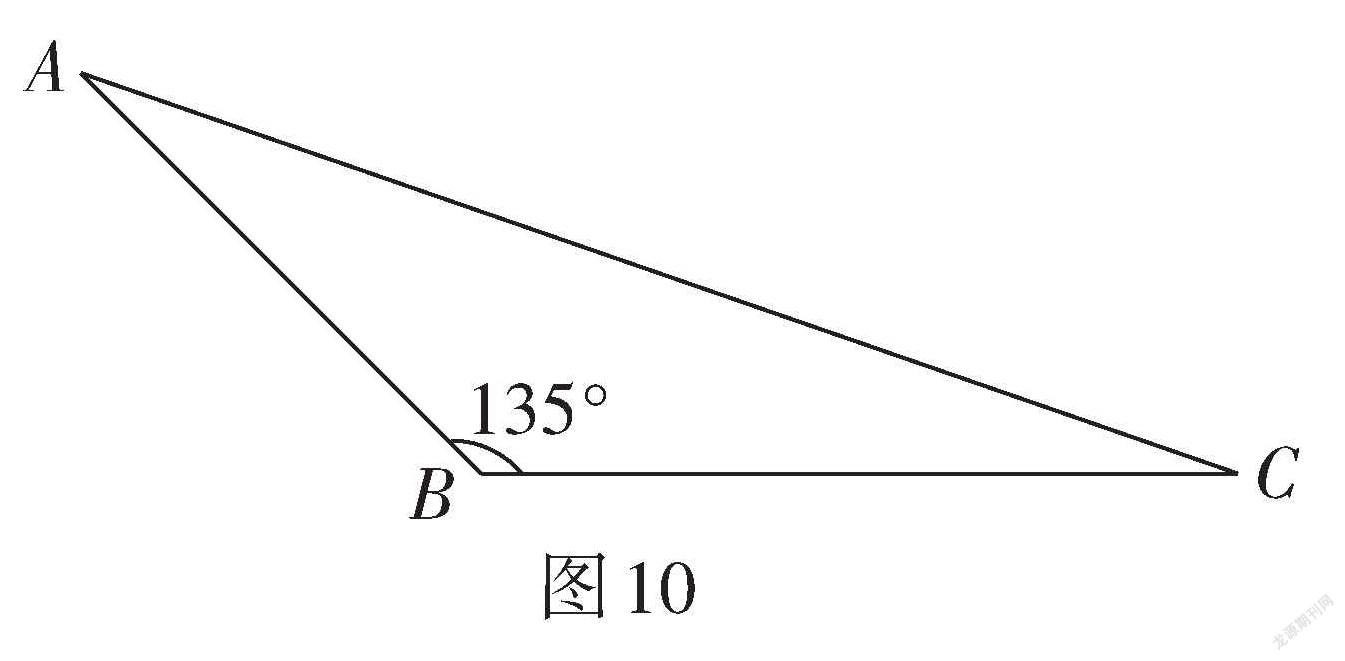
變式1：如圖10，在△ABC中， [AB=6，] [BC=8，][∠B=135°]，求[S△ABC].

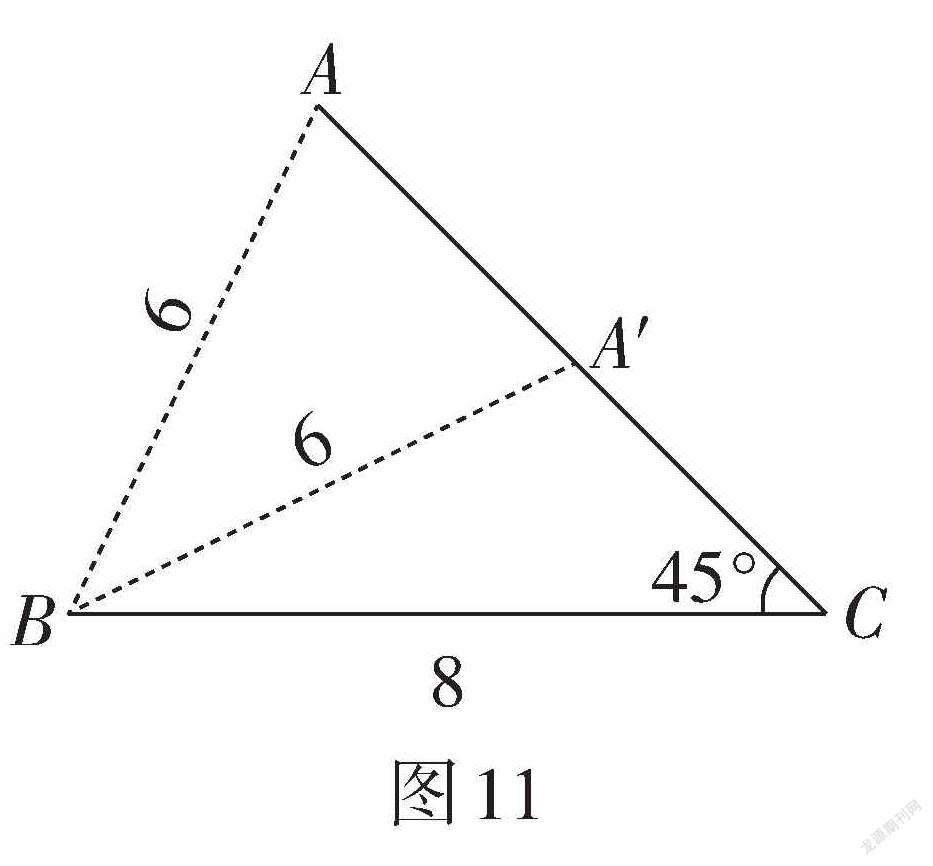
變式2：在△ABC中，[AB=6]，[BC=8]，[∠C=45°]，求[S△ABC].

變式3：在△ABC中，[AB=5]，[BC=8]，[AC=41]，求[S△ABC].

【設計意圖】例3已知兩邊及其夾角求三角形面積，可過點A或點C作三角形的高，利用三角函數求出高的值，進而求出三角形的面積. 變式1將銳角三角形改成鈍角三角形，解法與例3類似. 變式2已知兩邊及一邊的對角，求三角形面積，這時需分類討論（如圖11）. 變式3已知三邊求三角形面積，要構造直角三角形運用方程思想求解三角形的高，從而求得三角形的面積.

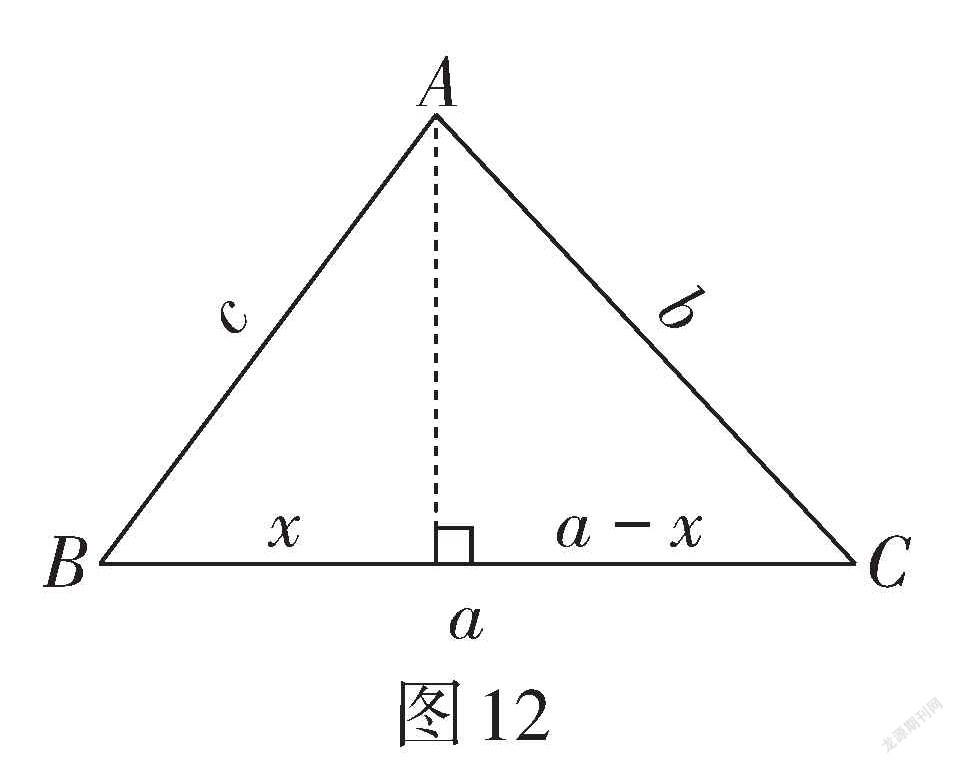
教師引導：本環節需要引導學生思考和解決在斜三角形中，已知三個元素求解其他邊、角及周長和面積等問題，解題時要充分利用特殊角. 可通過添加高線，把特殊角放到直角三角形中去. 而變式3需要先借助勾股定理知識求解有關邊，解題方法如下（如圖12），可列方程[c2-x2=b2-a-x2]，求得[x]，進而可得到三角形其他元素或面積.

片斷4：銳角三角函數的應用.

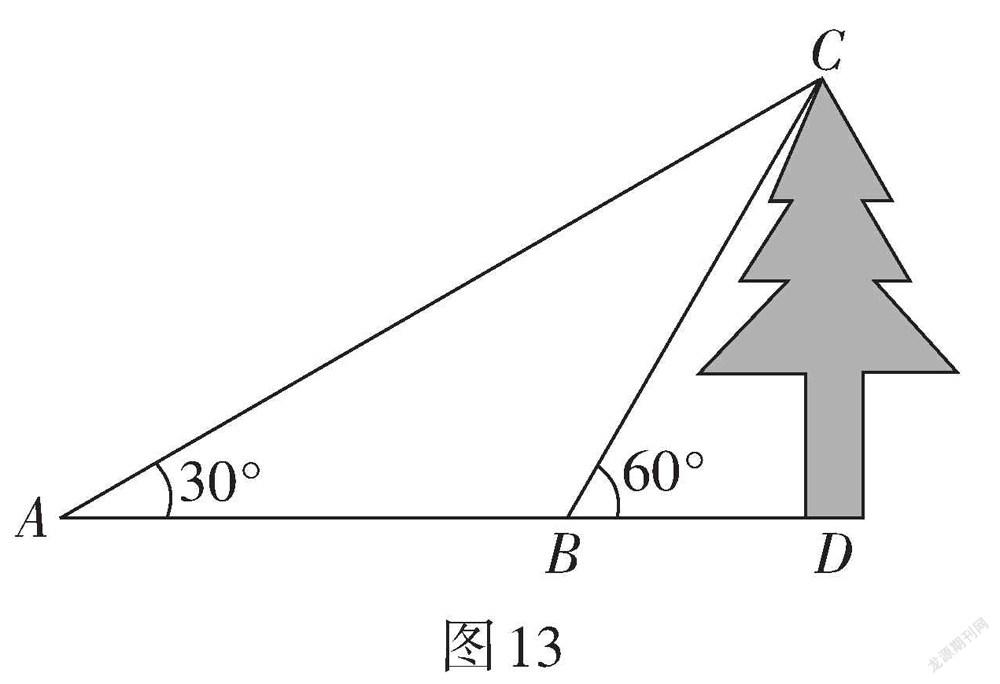
例4? 如圖13，某數學興趣小組想測量一棵樹CD的高度，他們先在點A處測得樹頂C的仰角為[30°]，然后沿AD方向前行10 m，到達點B，在點B處測得樹頂C的仰角為[60°]（A，B，D三點在同一直線上），試根據他們的測量數據計算這棵樹的高度.

變式1：如圖14，某數學興趣小組想測量一棵樹CD的高度，他們先在點A處測得樹頂C的仰角為[30°]，然后沿AD方向前行8 m，到達點B，在點B處測得樹頂C的仰角為[45°]（A，B，D三點在同一直線上），試根據他們的測量數據計算這棵樹的高度.

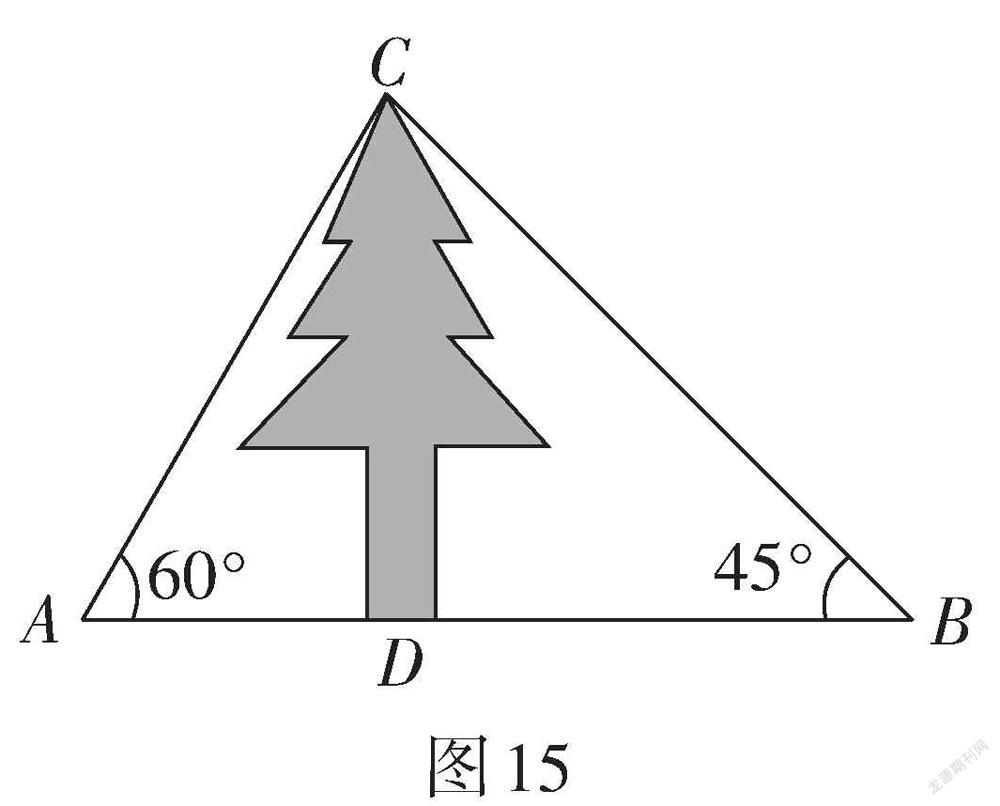
變式2：如圖15，某數學興趣小組想測量一棵樹CD的高度，他們先在點A處測得樹頂C的仰角為[60°]，然后沿AD方向前行15 m，到達樹的另一側點B，在點B處測得樹頂C的仰角為[45°]（A，B，D三點在同一直線上），試根據他們的測量數據計算這棵樹的高度.

【設計意圖】例4已知兩個仰角分別為[30°]和[60°]，可以利用外角性質得到[∠ACB=30°]. 從而得到[AB=][BC=10]. 再利用三角函數可求得樹高. 變式1將兩個仰角改為[30°]和[45°]時，直接求解樹高較為困難，可以運用方程思想，先設出樹高，則AD，BD的距離可以表示出來，再利用兩者關系即可列出方程求解. 變式2將觀測點改為樹的兩側，給學生提供另一種測量樹高的方法，也是銳角三角函數應用中的另一重要模型，經常可以用來測量樓高等問題，進一步拓展學生的思維，培養學生發現問題、提出問題、分析問題、解決問題的能力，解法上與變式1類似. 這幾道題看似相同，實則蘊含著不同的數學模型，有著不同的解題方法，通過一個簡單的測量樹高的問題，把零散的數學知識串聯起來，讓學生形成良好的知識結構，有效提高課堂教學效率.

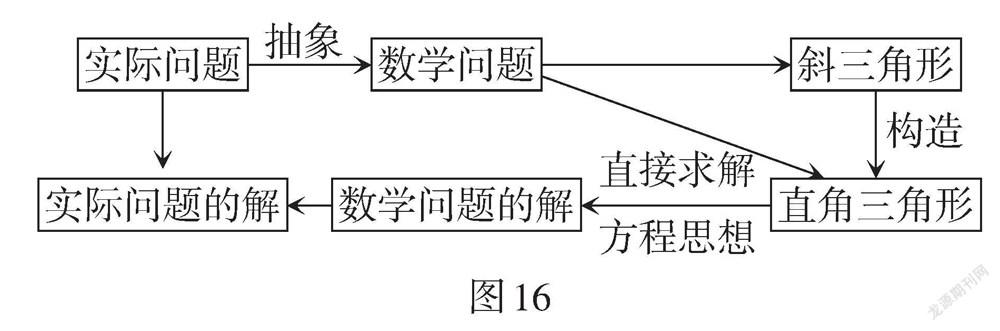
教師引導：通過以上變式，引導學生在利用銳角三角函數求解實際問題時，需先將實際問題抽象為數學問題，通過數學方法求解數學問題的解，再還原成實際問題的解. 同時，在求解時需正確理解仰角、俯角、坡角、方位角等相關概念. 在教師引導下，形成以下認知結構（如圖16）.

三、教學反思

在初三備考復習教學中，教師容易讓學生陷入“題海戰術”，讓課堂變得枯燥無味，缺乏對學生思維能力的培養，導致復習效率低下，學生學習的積極性下降. 而變式教學通過一圖多用、一題多變、多題重組，給人一種新鮮、生動的感覺，激發學生的學習興趣，提高學生學習的積極性.

變式教學由一個問題進行變式而衍生出相互關聯的問題鏈，引導學生多角度、多方位思考問題，通過總結反思，提煉解決問題的通性、通法，揭示問題本質，發展學生的數學建模和邏輯推理素養，拓展學生的思維，從而讓學生學會舉一反三、融會貫通、知識遷移，使原有孤立、零散的知識整體化，形成較為完整的認知結構，有效提高學生的學習效率.

對于數學學科核心素養的培養，變式教學有著很強的專業性和針對性，需要教師在數學教學中抓住問題的本質，創設合理的問題情境，啟發學生思維，滲透數學思想、數學方法，培養學生發現問題、分析問題、解決問題的能力，從而形成有助于學生終身和未來發展的核心素養.

參考文獻：

[1]黃悅軍. 關注基本模型? 形成解題程序? 提升核心素養：對一道中考題及其變式的解法探究[J]. 中學教研（數學），2019（1）：35-38.

[2]毛東良. 基于培養學生核心素養下的變式教學（二）[J]. 數學教學通訊（下旬），2016（6）：15-16.

[3]劉永東. 銳角三角函數及應用[J]. 中學數學教學參考（中旬），2019（1 / 2）：65-68.