“數學方法論”指導下的數學教學

摘? 要：做好數學教學，特別是幫助學生學會思考，十分重要的兩個環節是：（1）教師的“言傳身教”，用數學思維的分析帶動具體數學知識的教學;（2）解題教學，由單純的“就題論題”上升到“就題論法”和“就題論道”.

關鍵詞：數學方法論;數學教學;就題論法;就題論道

相對于其他論題而言，“數學方法論指導下的數學教學”應是大多數中學數學教師都較為熟悉的. 由于我國著名數學家徐利治先生的倡導，“數學方法論”早在20世紀80年代就已經走進了中學數學教師的視野，并已成為很多師范院校數學專業的一門專業課程. 更重要的是，中國的數學方法論研究從一開始就表現出了密切聯系實際數學教學這樣一個特點，即應當用數學思考的分析帶動具體數學知識（包括數學基礎知識與基本技能，下同）的教學，從而將數學課真正“教懂，教活，教深”，即向學生展現“活生生的”數學研究工作，而不是“死的”數學知識，并能幫助他們很好地理解相關內容，而不是囫圇吞棗，死記硬背. 使學生不僅能夠掌握具體的數學知識，也能夠很好地領會內在的思想方法.

筆者還有這樣一個具體建議：數學思維方法的學習，不應求全，而應求用. 從教學的角度來看，這就是指，無論是就“數學方法論”而言還是就“數學思維研究”而言，都不應成為借題發揮、紙上談兵的空洞學問，而應對實際教學工作發揮促進作用. 只有這樣，我們才能使學生真切地感受到數學思維的力量，從而真正起到“言傳身教”的作用.

總之，這方面工作最重要的一條原則是我們不應將數學思維的學習與具體數學知識的教學絕對割裂開來，而應十分重視用數學思維的分析帶動具體數學知識的教學，即應當特別重視數學思維在具體數學知識教學過程中的滲透與指導;我們還應通過這一途徑幫助學生逐步學會數學地思考，特別是使得相應的思維過程或方法對學生而言真正成為“可以理解的、可以學到手的和加以推廣應用的”.

當然，上面的論述并不排斥這樣一點：必要時我們也應適當進行數學思維的專門教學. 就現實而言，這也可被看成“解題教學”應當發揮的一個重要作用. 特別是相對于單純的“就題論題”，我們應當進一步上升到“就題論法”和“就題論道”.

應當強調的是，這里所說的“就題論道”有這樣一個含義，即我們應由單純強調“幫助學生學會數學地思考”過渡到“通過數學學會思考”. 相對于“用數學思考的分析帶動具體數學知識的教學”，后者可以說體現了一個更高的要求. 對此我們將在下一篇文章中圍繞“數學深度教學”做出具體論述.

最后，強調“解題教學”也反映了這樣一個認識：無論是就數學思維而言或是就一般性思維策略的學習而言，主要目標都是“能用”“會用”. 也正因如此，除去教師的直接示范外，我們應特別重視實踐中的學習. 特別是應當清楚地認識“問題解決”在這方面的重要作用. 例如，主要是在這樣的意義上，著名數學家哈爾莫斯指出，學習數學的唯一方法是做數學. 另外，正如曹廣福教授所指出的，就數學教育而論，思想當然是最重要的，但思想需要載體，領會一種思想更需要載體，否則思想就變成了虛無縹緲、不著邊際的夸夸其談……掌握一種思想更要親自實踐，看別人演示與自己實操是完全不同的，有時你聽起來似乎明白的東西，真正做起來就一籌莫展了，這就是缺少實踐的結果.

當然，又如先前的文章中已指出的，即使我們僅僅著眼于學生解決問題能力的提升，也不可能單純憑借大量練習實現，而是主要依靠主體的自覺總結、反思與再認識，包括教師的必要指導. 顯然，從這一角度我們可以更好地理解切實做好“解題教學”的重要性. 特別是我們應超越“就題論題”，從而上升到“就題論法”和“就題論道”，包括對于“總結、反思與再認識”的特別重視. 例如，從后一角度我們顯然可以更好地理解為什么應將“題后反思”看成“解題教學”十分重要的一環.

再者，“問題解決”當然又不應被看成“數學活動”（“數學實踐”）的唯一形式，而事實上這也就直接關系到了“問題解決”這一曾在世界范圍內廣泛實施的數學教育改革運動的局限性. 特別是我們是否應將“問題解決”看成學校數學教學的主要形式. 顯然，就目前的論題而言，這也更清楚地表明了切實做好以下工作的重要性，即我們不僅應當用數學思維的分析帶動具體數學知識的教學，也應通過教學幫助學生逐步學會學習，即由主要是在教師指導下進行學習逐步過渡到自主學習（后者正是“數學深度教學”的又一重要含義）.

由于“數學方法論指導下的數學教學”在我國已提倡多年，就這方面的具體工作而言，在此僅僅強調這樣幾點.

（1）正確處理數學思維與具體數學知識學習之間的關系，即應當用數學思維的分析帶動具體數學知識的教學，而不應將兩者絕對地割裂開來，或是始終停留于具體數學知識的學習中，卻未能上升到“思維與方法”這一更高層次，更不用說如何幫助學生逐步養成相應的“情感、態度與價值觀”.

（2）從同一角度我們也可更好地認識“問題引領”對于數學教學的特殊重要性，包括這樣一點：除去“知識的問題化”以外，后者還有更廣泛的含義與作用.

例如，正如波利亞所指出的，可能任何類型的思維守則都在于掌握和恰當地運用一系列合適的提問. 正因如此，我們就可將若干定型的問題（和建議）看成“數學啟發法”的核心. 這就是指只要問的是地方、是時候，就能起到“思想指南”的指導，可對人們克服面臨的困難提供一定的啟示或指明努力的方向.

進而，正如前面所提及的，除去“解題策略”的學習外，也直接關系到學生“元認知”水平的提升，以及我們又如何能夠通過提出新的問題實現認識的發展與深化.

當然，這也應被看成“認識的發展與深化”的又一重要含義，即我們應由單純的“問題解決”過渡到“就題論法”和“就題論道”，包括我們如何能夠切實提升學生在這方面的自覺性.

例如，在筆者看來，我們就應從上述角度更好地理解這樣一個論述：教師應是學習和問題解決的專家，教師的工作就是通過向學生問他們應當問自己的問題來對學習和問題解決進行指導和建模.

（3）相對于真實的數學發展歷史而言，相關工作主要又應被看成“數學史的方法論重建”，也就是我們如何能夠通過自己的探索，使得相應的發明創造對學生而言真正成為十分自然和可以理解的.

顯然，上述工作可被看成教學工作創造性質的重要體現. 特別是我們應圍繞自己的教學工作積極開展教學研究. 例如，如果我們在閱讀教材或實際教學的過程中發現某一內容的處理（包括教材中采取的途徑、別人設計的教案，以及自己先前使用過的教學設計）不是特別自然，這或許就可看成用思維方法的分析改進教學的一個很好的切入點，即我們應當通過自己的“再創造”，使之真正成為“可以理解的、可以學到手的和可以推廣應用的”.

以下就是這方面的一個具體實例，這也是筆者多年前的一個親身經歷.

案例1：三角形內角平分線的性質的證明.

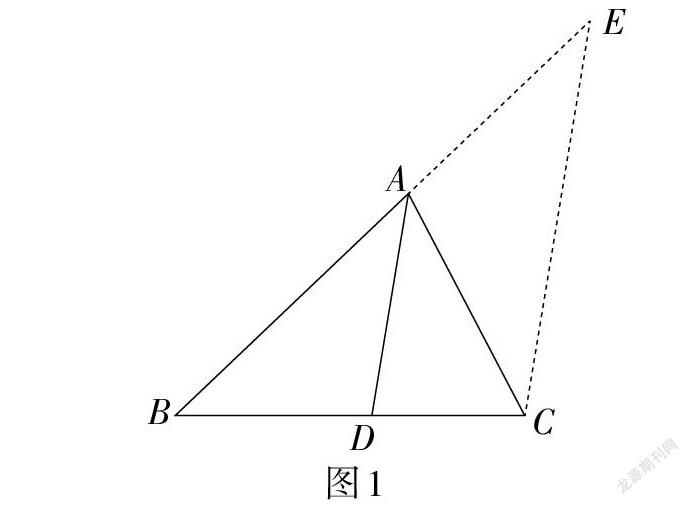
所謂“三角形內角平分線的性質”是指這樣一個定理：三角形中任何一個角的平分線分對邊所得的兩條線段與這個角的兩邊對應成比例. 教材中關于這一定理的證明并不困難（如圖1），但這恰恰又是我們在從事這一內容的教學時應當深入思考的一個問題：相關的證明思路是如何發現的？我們如何能夠使得這一過程對學生而言真正成為十分自然的？因為，不可否認的是，CE這一輔助線的添加是很難想到的，從而就很像波利亞所說的“從帽子中掏出來的兔子”.

圍繞上述問題，筆者進行了長期思考，但始終未能得出令人滿意的答案，直至有一天突然產生了這樣一個想法：既然無法自然而然地引出所說的輔助線，那么我們是否可以不添加任何輔助線直接證明這一定理呢？又由于筆者在此前剛剛接觸到了所謂的“面積法”，即主要通過對圖形面積的分析求解幾何問題. 這樣，以下證明思路的產生就十分自然了.

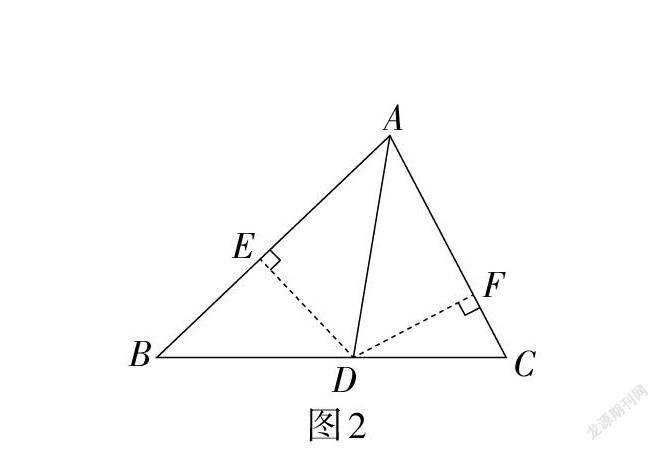
如圖2，作為面積法的直接應用，我們在此集中考查△ABD與△ADC的面積比. 由于這兩個三角形具有同一條高，因此它們的面積比顯然就等于BD∶DC;另外，由于AD是角平分線，所以AD上的任意一點到角兩邊的距離相等. 由此我們可以立即推出：△ABD的面積∶△ADC的面積 = （AB·DE）∶（AC·DF） = AB∶AC. 這樣，相關的定理（BD∶DC = AB∶AC）就得到了證明.

當然，作為教學活動，我們又不應滿足于這一問題的解決，而應引導學生從更一般的角度進行分析、思考，即應當由知識和技能的學習上升到思維的層面. 例如，通過上述解題活動我們顯然可以幫助學生很好地理解“面積法”的具體含義，包括通過這一方法與傳統方法的比較更好地認識它們各自的優點與局限性，從而就可以在應用上實現更大的自覺性.

感興趣的讀者還可對以下問題做出自己的思考和探究.

案例2：“直角三角形斜邊上的中線等于斜邊的一半”的證明.

這是八年級的一項學習內容. 由于學生在先前已經學習了“三角形的全等”和“等腰三角形的性質”，因此面對以下證明在理解上就不會有太大困難.

如圖3，在Rt△ABC中，∠ACB是直角. 在∠ACB內作∠BCD = ∠B，CD與AB相交于點D，可知DB = DC. 依據等角的余角相等，可得∠ACD = ∠A. 于是就有DA = DC. 從而就有DA = DB = DC. 由于CD是斜邊AB上的中線，且CD =[12]（DA +

DB） =[12]AB. 這樣，原來的定理就得到了證明.

現在的問題是：在證明的過程中我們為什么不直接作出斜邊AB上的中線CD，而非要把它看成按照“∠BCD = ∠B”這一要求作的另一條線呢？盡管這樣做后證明不會有任何困難，但從思維的角度來看畢竟很不自然！

筆者的希望是：能否為上述定理找出一個更加自然的證明？

以下再針對我們應當如何做好“解題教學”提出若干具體建議.

（1）這方面工作應當堅持這樣一個立場，即對于“題海戰術”的明確反對. 但是，我們應如何看待“問題的適當分類與辨識”這樣一項工作？由于后者在各方面都有重要應用，我們對此就應持肯定的態度;但在做出這一肯定的同時，我們又應注意防止題型的“泛化”，以及對于“機械記憶與簡單模仿”的不恰當強調，即應當注意題型選擇的“少而精”，并應通過“變式理論”的應用與抽象分析很好地實現“講一題，通一類，得一法”，包括引導學生從多個不同角度進行分析和思考，包括必要的比較、變化與更高層次的綜合等.

進而，從宏觀的角度來看，我們應認真思考是否應在所有的知識點上都要學生做很多作業，乃至各種各樣的難題？恰恰相反，我們應當通過認真的學習和研究很好地弄清楚什么是其中的重點和難點，切實做好作業的整體設計，包括以此作為審題，特別是對于來自各種渠道的題目做出選擇并重新加以組織的主要標準，即真正做好“分清主次，突出重點，以主帶次”.

（2）集中于“解題策略”是國內“解題研究”的一個重要特點. 現實中存在解題策略的“細化”這樣一個普遍傾向，乃至對于“解題活動算法化、程序化”的不恰當強調. 筆者認為，我們應注意糾正這樣一個傾向. 因為，如果缺乏自覺性的話，我們就很可能在不知不覺中重新回到“題海”與“術林”之中;再者，這事實上也可被看成國外的相關研究給予我們的一個重要啟示，即上述方向的努力并不能有效提高人們的解題能力. 相信讀者由以下關于思維活動性質的分析即可很好地認識到這樣一點.

由于數學問題的多樣性和復雜性，更由于思維活動的非邏輯性，即不僅可能表現為純粹的靈感或頓悟，并必然具有一定的或然性與個體性. 因此，盡管我們應當充分肯定“題型分析”的重要性，努力提升學生的辨識能力，很好地掌握相應的“解法”，也應高度重視解題策略與數學思想方法的學習，從而在遇到困難時就可獲得一定的啟示. 但是，單靠這些顯然不足以保證解題活動的成功. 恰恰相反，我們應由具體的數學思想方法和解題策略轉向一般性思維策略與思維品質的提升.

后者事實上也就是“就題論道”的主要含義. 對此，我們也將在下一篇文章中做出進一步的分析和論述.

（3）努力提升學生在這方面的自覺性，包括：我們為什么應當積極從事“解題活動”？這方面的具體實踐應特別重視哪些方面或問題？等等. 例如，正如前面所提及的，我們不僅應當幫助學生很好地認識“題后反思”的重要性，也應努力提升自身的“元認知”水平. 因為，后者不僅是決定人們解題活動能否成功的一個重要因素，更是我們在這方面是否具有較大自覺性的一個重要表現.

還應提及的是，這正是中國“解題研究”的又一重要特色，即對思維活動辯證性質的突出強調. 例如，所謂的以退求進、正難則反;分合并用、進退互化、正反相輔、動靜轉換、數形結合、以美啟真…… 顯然，這事實上十分有益于提升我們在解題活動中的自覺性.

（4）堅持教學的開放性. 這不僅可以被看成充分尊重學生個體特征的一個必然結論，也可被看成辯證思維的又一重要表現. 后者是指我們既應明確肯定教學工作的規范性質，努力幫助學生實現思維的必要優化，也應很好地處理規范性與開放性之間的關系. 因為，歸根結底地說，數學教育的基本目標應是促進學生思維的發展，而不是將此硬性納入任一固定的框架. 這更應被看成發明創造的真諦所在——“以正合，以奇勝”.

最后，應當再次提及的是，無論就“數學方法論指導下的數學教學”而言，或是就“解題教學”而言，“深度教學”都體現了更高的要求. 這正是下一篇文章的直接論題.

參考文獻：

[1]鄭毓信. 數學方法論[M]. 南寧：廣西教育出版社，1991.

[2]曹廣福. 中學數學教育中的若干問題[J]. 教育研究與評論，2020（2）：9-15.

[3]喬治·波利亞. 數學的發現（第二卷）[M]. 劉景麟，曹之江，鄒清蓮，譯. 呼和浩特：內蒙古人民出版社，1980.

[4]戴維·H.喬納森. 學習環境的理論基礎[M]. 鄭太年，任友群，譯. 上海：華東師范大學出版社，2002.

[5]戴再平. 數學習題理論[M]. 上海：上海教育出版社，1991.

[6]羅增儒. 數學解題學引論[M]. 西安：陜西師范大學出版社，1997.