分析重抓手　解題謀策略

蔡世英　陳中峰

摘? 要：“抽樣與數據分析”是運用統計思想解決實際問題的重要一環. 文章摘選了2021年全國各地中考部分“抽樣與數據分析”中考試題進行試題分析、解法分析，梳理題型，分析試題特點，歸納試題解法，凝練統計素養的基本要求，落實應用意識，提升學生的數據分析能力.

關鍵詞：中考試題;試題分析;解法分析;解法賞析

抽樣與數據分析是為了提取有用信息和形成結論而對數據加以詳細研究和概括總結的過程. 2021年全國各地中考“抽樣與數據分析”試題的考查根據《義務教育數學課程標準（2011年版）》（以下簡稱《標準》）的要求，注重在實際生活情境下對數據進行收集、整理、描述、分析和應用，滲透數學問題的應用意識，關注數據分析素養的養成，感悟統計分析的數學理念. 本文摘選了2021年全國各地中考試題中“抽樣與數據分析”部分試題進行分析、歸納與總結，以饗讀者.

一、試題分析

1. 立足概念理解，關注知識遷移

《標準》指出，學好數學知識應在理解的基礎上和知識的應用中不斷鞏固和深化對數學知識的理解，從而達到知識的遷移. 2021年全國各地中考“抽樣與數據分析”試題能注重基本概念的考查，對平均數、眾數、中位數和方差的意義等基本概念進行考查，此類試題解題的關鍵是能精準掌握概念，精確使用公式，綜合運用統計知識解題.

例1 （湖南·衡陽卷）為了向建黨一百周年獻禮，某市中小學生開展了紅色經典故事演講比賽. 某參賽小組6名同學的成績（單位：分）分別為：85，82，86，82，83，92. 關于這組數據，下列說法錯誤的是（? ? ）.

（A）眾數是82 （B）中位數是84

（C）方差是84 （D）平均數是85

【評析】此題考查了平均數、眾數、中位數和方差的意義. 平均數是指在一組數據中所有數據之和除以數據的個數;眾數是指一組數據中出現次數最多的數據;中位數是指將一組數據從小到大（或從大到小）重新排列后，最中間的那個數（或最中間兩個數的平均數）;方差是指一組數據中各數據與它們的平均數的差的平方的平均數. 若能理解平均數、眾數、中位數和方差的意義，則容易得到答案，此題答案為選項C.

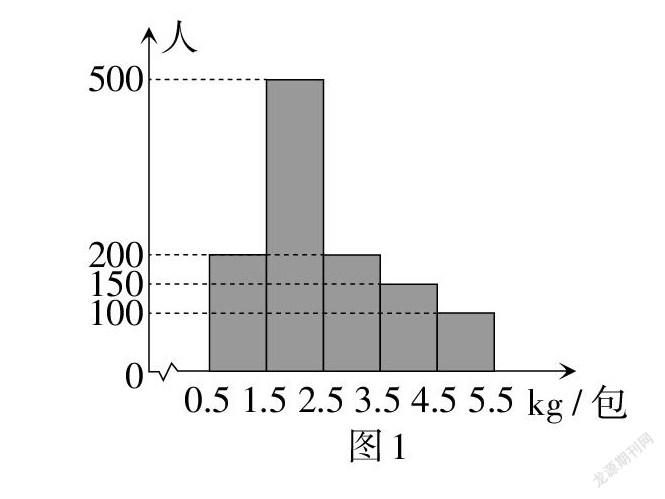
例2 （上海卷）商店準備一種包裝袋來包裝大米，經市場調查以后，作出如圖1所示的統計圖，試問選擇什么樣的包裝最合適（? ? ）.

（A）2 kg / 包 （B）3 kg / 包

（C）4 kg / 包 （D）5 kg / 包

【評析】此題考查了條形統計圖及眾數的概念，要求學生具備讀圖能力. 由圖象的信息及眾數的概念容易知道，眾數落入的范圍是1.5 kg～2.5 kg，從選項中容易確定符合題意的答案. 先確定眾數的大致位置，再決定具體哪個數是眾數，此題的考法讓人耳目一新，需要對眾數的知識概念進行遷移，符合“能利用頻數分布直方圖解釋數據中蘊含的信息”的《標準》要求. 故此題答案為選項A.

2. 立足統計方式，關注解法選擇

2021年全國各地中考“抽樣與數據分析”試題考查實際問題情境下統計方式的選擇與使用，以及統計量的現實意義，要求學生能掌握相關統計量的計算方法，并注意解法的歸納.

例3 （福建卷）某校為推薦一項作品參加“科技創新”比賽，對甲、乙、丙、丁四項候選作品進行量化評分，具體成績（百分制）如表1所示.

如果按照創新性占60%、實用性占40%計算總成績，并根據總成績擇優推薦，那么應推薦的作品是（? ? ）.

（A）甲 （B）乙

（C）丙 （D）丁

【評析】此題以“科技創新”比賽為背景命制試題，考查了運用加權平均數解決實際問題，旨在引導學生于“德智體美勞”五育中全面發展. 方法1：通過甲、丙、丁的成績對比可先去掉甲與丁，直接比較乙與丙，由創新性的權重大于實用性的權重，可知乙的總成績必然大于丙的總成績. 方法2：計算出四人的總成績分別為90，93，92，88，易知乙的總成績最高，故此題答案為選項B.

例4 （內蒙古·鄂爾多斯卷）小明收集了鄂爾多斯市某酒店2021年3月1日～3月6日每天的用水量（單位：噸），整理并繪制成如圖2所示的折線統計圖，下列結論正確的是（? ? ）.

下列關于成績的統計量中，與被遮蓋的數據無關的是（? ? ）.

（A）平均數，方差 （B）中位數，方差

（C）中位數，眾數 （D）平均數，眾數

【評析】此題以建黨一百周年黨史知識競賽為背景命制，以缺失部分數據的不完整表格作為已知條件，解題的關鍵是計算出被遮蓋的數據和. 容易發現，表格中成績數據排列已按從小到大的順序排列，被遮蓋的兩個數據91分、92分的人數和為3，成績為100分的人數出現次數最多，因此成績的眾數是100. 成績從小到大排列后處在第25，26位的兩個數都是98，因此中位數是98，中位數和眾數與被遮蓋的數據無關，故此題答案為選項C.

3. 立足“三圖一表”，關注圖表閱讀

初中統計圖表主要體現為“三圖一表”，即折線統計圖、條形統計圖、扇形統計圖，以及統計表. 各種統計圖表都有各自的特點，在實際生活中有不同的應用. 2021年全國各地中考試題在統計圖表方面的考查仍然體現在統計圖表之間的相互聯系，須經過讀圖、識圖獲得信息，畫（補）圖分析數據，經歷收集、整理、描述和分析數據的活動，同時了解數據處理的必要性.

例6 （湖北·隨州卷）圖3是小明某一天測得的7次體溫情況的折線統計圖，下列信息不正確的是（? ? ）.

（A）測得的最高體溫為37.1℃

（B）前3次測得的體溫在下降

（C）這組數據的眾數是36.8

（D）這組數據的中位數是36.6

【評析】此題考查了折線統計圖，眾數與中位數的計算方法，以及學生的讀圖與析圖能力. 從圖中容易知道選項A、選項B正確，且出現次數最多的數據36.8是眾數，故選項C也正確. 中位數是指排序后最中間的數據，即排序后第4個數據36.8是中位數，則選項D不正確，故此題答案為選項D.

例7 （湖北·黃岡卷）高爾基說：“書，是人類進步的階梯.”閱讀可以豐富知識，拓寬視野，給我們帶來愉悅. 英才中學計劃在各班設立圖書角，為合理搭配各類書籍，對全校學生進行抽樣調查，收集整理喜愛的書籍類型（A. 科普，B. 文學，C. 體育，D. 其他），繪制出如圖4、圖5所示的兩幅不完整的統計圖，則下列說法錯誤的是（? ? ）.

（A）樣本容量為400

（B）類型D所對應的扇形的圓心角為36°

（C）類型C所占百分比為30%

（D）類型B的人數為120人

【評析】此題以設立圖書角為背景命制，以統計圖的方式呈現數據，考查樣本容量、頻數、頻率的關系，以及統計數據之間的相互轉換，需要具備一定的讀圖、識圖及分析推理能力. 根據A類100人占25%可計算出樣本容量為400，根據D類占10%可計算其所對扇形的圓心角度數為[36°]，根據C類140人 ÷ 總樣本容量400即可得所占百分比[35%]，故選項C錯誤，總樣本容量減去A，C，D三類人數即可得B類人數120人. 此題答案為選項C.

例8 （湖南·邵陽卷）某社區針對5月30日前該社區居民接種新冠疫苗的情況開展了問卷調查，共收回6 000份有效問卷.經統計，制成如表3所示的數據表格.

小杰同學選擇扇形統計圖分析接種不同針數的居民人數所占總人數的百分比.下面是制作扇形統計圖的步驟（順序打亂）：

① 計算各部分扇形的圓心角分別為[126°]，[136.8°]，[79.2°]，[18°].

② 計算出接種不同針數的居民人數占總人數的百分比分別為35%，38%，22%，5%.

③ 在同一個圓中，根據所得的圓心角度數畫出各個扇形，并注明各部分的名稱及相應的百分比.

如圖6，制作扇形統計圖的步驟排序正確的是（? ? ）.

（A）②①③ （B）①③②

（C）①②③ （D）③①②

【評析】此題考查扇形統計圖的制作步驟，根據制作步驟即可求解. 通過考查抽樣調查中制作圖表的具體制作程序，此類試題具有可操作性的實際意義，此題答案為選項A.

4. 立足實際案例，強化應用意識

數學知識是解決實際問題的工具，尤其是統計知識與實際生活密切相關. 2021年全國各地區中考試題中不乏運用數學知識解決實際問題的試題，而“抽樣與數據分析”知識最能體現數學在日常生活中的應用價值.

例9 （浙江·臺州卷）超市貨架上有一批大小不一的雞蛋，某顧客從中選購了部分大小均勻的雞蛋，設貨架上原有雞蛋的質量（單位：g）平均數和方差分別為[x]，[s2]，該顧客選購的雞蛋的質量平均數和方差為[x1]，[s21]，則下列結論一定成立的是（? ? ）.

【評析】此題以顧客在超市中選購雞蛋為背景命制，顧客所選購的雞蛋大小均勻，即雞蛋質量數據比較整齊，可推斷相應的方差[s21]一定比貨架上原有雞蛋質量數據的方差[s2]小，則一定成立的是[s2>s21]. 故此題答案為選項C.

例10 （湖南·常德卷）舒青是一名觀鳥愛好者，他想要用折線統計圖來反映中華秋沙鴨每年秋季到當地避寒越冬的數量變化情況，以下是排亂的統計步驟：① 從折線統計圖中分析出中華秋沙鴨每年來當地避寒越冬的變化趨勢;② 從當地自然保護區管理部門收集中華秋沙鴨每年來當地避寒越冬的數量記錄;③ 按統計表的數據繪制折線統計圖;④ 整理中華秋沙鴨每年來當地避寒越冬的數量并制作統計表.正確統計步驟的順序是（? ? ）.

（A）②→③→①→④

（B）③→④→①→②

（C）①→②→④→③

（D）②→④→③→①

【評析】此題考查制作折線統計圖的實際操作步驟，具有現實意義. 根據數據的收集、整理、制作折線統計圖及由統計圖分析結果等步驟可得答案. 此題答案為選項D.

例11 （黑龍江·綏化卷）近些年來，移動支付已成為人們的主要支付方式之一. 某企業為了解員工某月A，B兩種移動支付方式的使用情況，從企業2 000名員工中隨機抽取了200人，發現樣本中A，B兩種支付方式都不使用的有10人，樣本中僅使用A種支付方式和僅使用B種支付方式的員工支付金額a（元）分布情況如表4所示.

下面有四個推斷：

① 根據樣本數據估計，企業2 000名員工中，同時使用A，B兩種支付方式的為800人;

② 本次調查抽取的樣本容量為200人;

③ 樣本中僅使用A種支付方式的員工，該月支付金額的中位數一定不超過1 000元;

④ 樣本中僅使用B種支付方式的員工，該月支付金額的眾數一定為1 500元.

其中正確的是（? ? ）.

（A）①③ （B）③④

（C）①② （D）②④

【評析】此題考查數據的簡單隨機抽樣，體會抽樣的必要性. 涉及的統計知識有樣本容量、中位數、眾數等核心內容. 在①中，體會用樣本估計總體的思想，需具備推斷能力，先求得樣本中同時使用A，B兩種支付方式的有80人;在②中，由已知可知樣本容量為200，但樣本容量無單位;在③中，利用中位數的定義可以直接判斷;在④中，根據眾數的定義可以直接判斷.此題答案為選項A.

二、解法分析

中考有關“抽樣與數據分析”部分的試題大都比較容易，但由于要以實際生活背景設置試題，這就要求學生要有一定的閱讀能力，要有讀圖、識圖、析圖、分析與應用知識的能力. 如何突破這一難點？靈活運用統計的相關知識準確地找到解題的切入點顯得尤為重要. 在解題方面，筆者認為應該重視以下三“從”，即“從概念理解入手，掌握基本題型”“從讀圖、識圖切入，突破閱讀障礙”“從培養數據推斷著手，提升決策能力”.

1. 從概念理解入手，掌握基本題型

統計概念是數學思維的細胞，它是進行數學推理、判斷及說理的依據. 2021年全國各地中考試題中，對統計部分的考查比較注重貼近生活實際. 在解決此類問題時，要注意結合實際背景理解基本的統計概念原理，選擇合適的數據調查方式、采用貼切的數據描述手段，選用合理的數據統計量，掌握基本的統計試題類型.

例12 （山東·臨沂卷）實施鄉村振興計劃以來，我市農村經濟發展進入了快車道，為了解梁家嶺村今年一季度經濟發展狀況，小玉同學的課題研究小組從該村300戶家庭中隨機抽取了20戶，收集到他們一季度家庭人均收入的數據如下（單位：萬元）：

0.69? 0.73? 0.74? 0.80? 0.81? 0.98? 0.93? 0.81

0.89? 0.69? 0.74? 0.99? 0.98? 0.78? 0.80? 0.89

0.83? 0.89? 0.94? 0.89

研究小組的同學對以上數據進行了整理分析，得到表5、表6.

【評析】此題考查頻數、中位數、眾數、樣本估計總體等相關統計知識. 在第（1）小題中，根據所給數據計數，即可得[a]，[b]的值. 根據中位數和眾數的定義求解，可得[c]，[d]的值. 在第（2）小題中，采用樣本估計總體的方法，可求出今年一季度梁家嶺村家庭人均收入不低于0.8萬元的戶數所占的百分比，即可得到結論. 在第（3）小題中，根據中位數進行判斷即可.

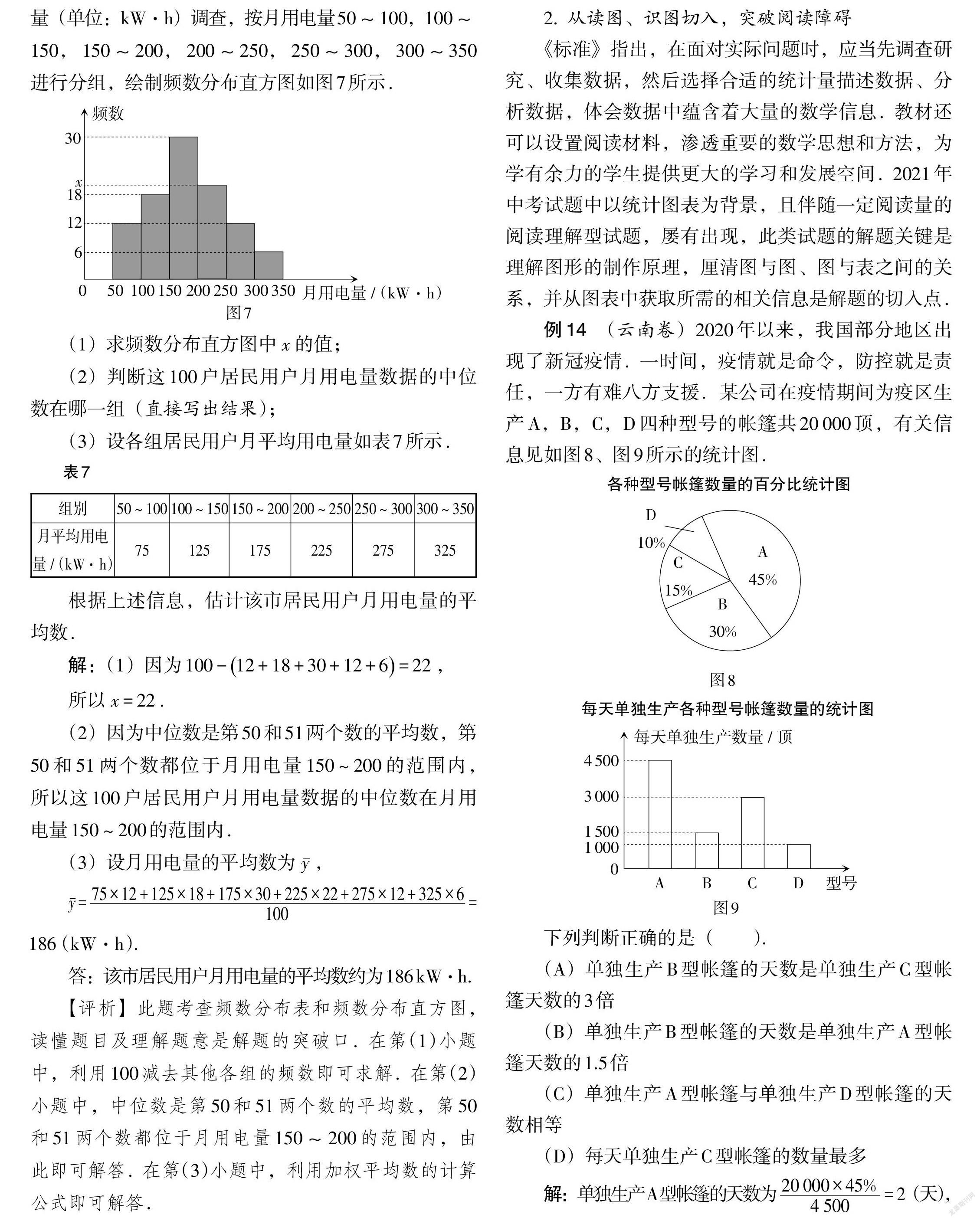
例13 （安徽卷）為了解全市居民用戶用電情況，某部門從居民用戶中隨機抽取100戶進行月用電量（單位：kW·h）調查，按月用電量50～100，100～150，150～200，200～250，250～300，300～350進行分組，繪制頻數分布直方圖如圖7所示.

（1）求頻數分布直方圖中[x]的值;

（2）判斷這100戶居民用戶月用電量數據的中位數在哪一組（直接寫出結果）;

（3）設各組居民用戶月平均用電量如表7所示.

根據上述信息，估計該市居民用戶月用電量的平均數.

解：（1）因為[100-12+18+30+12+6=22]，

所以[x=22].

（2）因為中位數是第50和51兩個數的平均數，第50和51兩個數都位于月用電量150～200的范圍內，所以這100戶居民用戶月用電量數據的中位數在月用電量150～200的范圍內.

（3）設月用電量的平均數為[y]，

答：該市居民用戶月用電量的平均數約為[186]kW·h.

【評析】此題考查頻數分布表和頻數分布直方圖，讀懂題目及理解題意是解題的突破口. 在第（1）小題中，利用100減去其他各組的頻數即可求解. 在第（2）小題中，中位數是第50和51兩個數的平均數，第50和51兩個數都位于月用電量150～200的范圍內，由此即可解答. 在第（3）小題中，利用加權平均數的計算公式即可解答.

2. 從讀圖、識圖切入，突破閱讀障礙

《標準》指出，在面對實際問題時，應當先調查研究、收集數據，然后選擇合適的統計量描述數據、分析數據，體會數據中蘊含著大量的數學信息. 教材還可以設置閱讀材料，滲透重要的數學思想和方法，為學有余力的學生提供更大的學習和發展空間. 2021年中考試題中以統計圖表為背景，且伴隨一定閱讀量的閱讀理解型試題，屢有出現，此類試題的解題關鍵是理解圖形的制作原理，厘清圖與圖、圖與表之間的關系，并從圖表中獲取所需的相關信息是解題的切入點.

例14 （云南卷）2020年以來，我國部分地區出現了新冠疫情. 一時間，疫情就是命令，防控就是責任，一方有難八方支援.某公司在疫情期間為疫區生產A，B，C，D四種型號的帳篷共20 000頂，有關信息見如圖8、圖9所示的統計圖.

下列判斷正確的是（? ? ）.

（A）單獨生產B型帳篷的天數是單獨生產C型帳篷天數的3倍

（B）單獨生產B型帳篷的天數是單獨生產A型帳篷天數的1.5倍

（C）單獨生產A型帳篷與單獨生產D型帳篷的天數相等

（D）每天單獨生產C型帳篷的數量最多

解：單獨生產A型帳篷的天數為[20 000×45%4 500=2 ]（天），

單獨生產B型帳篷的天數為[20 000×30%1 500=4]（天），

單獨生產C型帳篷的天數為[20 000×15%3 000=1]（天），

單獨生產D型帳篷的天數為[20 000×10%1 000=2]（天），

容易知道選項A、選項B均不正確.

每天單獨生產A型帳篷的數量最多，顯然選項D也不正確.

故此題答案為選項C.

【評析】此題考查了扇形統計圖與條形統計圖，須從兩種統計圖中獲取相關信息，再計算出相關的量.

例15 （湖南·株洲卷）目前，國際上常用身體質量指數“[BMI]”作為衡量人體健康狀況的一個指標，其計算公式[BMI=Gh2]（G表示體重，單位：千克;[h]表示身高，單位：米）. 已知某區域成人的[BMI]數值標準為[BMI<16]為瘦弱（不健康）;[16]≤[BMI]<[18.5]為偏瘦;[18.5]≤[BMI][<24]為正常;[24]≤[BMI][<28]為偏胖;[BMI]≥[28]為肥胖（不健康）. 某研究人員從該區域的一體檢中心隨機抽取55名成人的體重、身高數據組成一個樣本，計算每名成人的[BMI]數值后統計如表8和圖10所示.

【評析】此題考查了隨機抽樣、統計表和條形統計圖. 在第（1）小題中，可直接從圖表中獲取數據. 在第（2）小題中，根據公式直接代入求值. 在第（3）小題中，從圖象中獲取“[n<4]”這一信息，結合“[n]≥[2]（[n]為正整數）”，得“[n=2]或[n=3]”是解題的關鍵，再根據抽取人數為55可計算出[m]的值.

3. 從培養數據推斷著手，提升決策能力

《標準》指出，要能解釋統計結果，根據結果做出簡單的判斷和預測，并能進行交流.

學習統計不能僅局限于純粹地讀題、析題與解題，更重要的是，面對實際問題時要有統計意識，用統計的思想方法思考問題，再根據統計知識推斷或幫助我們提升對實際問題的決策能力.

例16 （湖南·永州卷）某初級中學堅持開展陽光體育活動，七年級至九年級每學期均進行體育技能測試. 其中A班甲、乙兩位同學6個學期的投籃技能測試成績（投籃命中個數）折線圖如圖11所示. 為參加學校舉行的畢業籃球友誼賽，A班需從甲、乙兩位同學中選1人進入班球隊，從兩人成績的穩定性考慮，決策A班應該選擇的同學是______.

故甲投籃技能測試成績數據比較穩定.

故填甲.

【評析】此題考查折線統計圖與方差的意義，體會刻畫數據離散程度的統計量在實際中的應用.

例17 （江蘇·南京卷）某市在實施居民用水定額管理前對居民生活用水情況進行了調查，通過簡單隨機抽樣獲得了100個家庭去年的月均用水量數據，將這組數據按從小到大的順序排列，其中部分數據如表9所示.

（1）求這組數據的中位數.已知這組數據的平均數為9.2 t，你對它與中位數的差異有什么看法？

（2）為了鼓勵節約用水，要確定一個用水量的標準，超出這個標準的部分按1.5倍價格收費，若要使75%的家庭水費支出不受影響，你覺得這個標準應該定為多少？

解：（1）由表格數據可知，位于最中間的兩個數分別是6.4和6.8.

故中位數為[6.4+6.82=6.6]（t）.

而這組數據的平均數為9.2 t，它們之間差異較大，主要是由它們各自的特點決定的，主要原因如下.

① 平均數與每一個數據都有關，任何數據的變動都會引起平均數的相應變動;主要缺點是易受極端值的影響，這里的極端值是指偏大或偏小數，當出現偏大數時，平均數將會被抬高，當出現偏小數時，平均數將會降低.

② 將數據按照從小到大或從大到小的順序排列. 如果數據個數是奇數，則處于最中間位置的數就是這組數據的中位數;如果數據的個數是偶數，則中間兩個數據的平均數是這組數據的中位數. 它的求出不需要或只需簡單地計算，不受極端值的影響.

這100個數據中，最大的數據是28，最小的數據是1.3，

因此，平均數受到極端值的影響，造成與中位數差異較大.

（2）因為第75戶用水量為11 t，第76戶用水量為13 t，因此標準應定為11 ≤ a < 13（其中a為標準用水量，單位：t）.

【評析】（1）從中位數和平均數的定義和計算公式的角度分析它們的特點，可找出它們差異的原因;（2）從表中找到第75戶和第76戶家庭的用水量，則可得到應制定的用水量標準數據.

三、試題解法賞析

《標準》指出，要讓學生感受解決問題策略的多樣化與靈活性，并比較不同方法的特點. 2021年全國各地中考試題“抽樣與數據分析”部分有立意新穎的靚麗好題，此類試題有助于拓寬學生的解題思路，培養發散思維. 因篇幅所限，現略舉一二.

1. 解法的多樣性

例18 （河北卷）小明調查了本班每位同學最喜歡的顏色，并繪制了不完整的扇形圖（如圖12）及條形圖（如圖13）（柱的高度從高到低排列）. 條形圖不小心被撕了一塊，圖13中“（ ? ?）”應填的顏色是（? ? ）.

故此題答案為選項D.

（方法2）事實上，只要緊緊抓住“條形統計圖中柱的高度從高到低排列”這個關鍵信息，然后直接量出扇形中各部分圓心角的度數，再找到度數為倒數第二位位置的扇形所對應的顏色，故此題答案為選項D.

【評析】根據柱的高度從高到低排列與扇形所占的百分比，可知藍色是5，且所占的百分比是10%. 可求出調查的總人數，用16除以總人數得出所占的百分比. 從而排除最多人數16的條形是紅色，再根據紅色所占的百分比求出喜歡紅色的人數，用總人數減去其他人數，求出另一組的人數，最后根據柱的高度從高到低排列，可求得答案.

例19 （浙江·溫州卷）某校將學生體質健康測試成績分為A，B，C，D四個等級，依次記為4分，3分，2分，1分.為了解學生整體體質健康狀況，擬抽樣進行統計分析.

（1）以下是兩位同學關于抽樣方案的對話.

小紅：我想隨機抽取七年級男、女生各60人的成績.

小明：我想隨機抽取七、八、九年級男生各40人的成績.

根據學校信息，試簡要評價小紅、小明的抽樣方案. 如果你來抽取120名學生的測試成績，試給出抽樣方案.

（2）現將隨機抽取的測試成績進行整理，并繪制成如圖14所示的統計圖，試求出這組數據的平均數、中位數和眾數.

解：（1）兩人都能根據學校信息合理選擇樣本容量進行抽樣調查.

小紅的方案考慮到了性別的差異，但沒有考慮到年級、學段的差異;

小明的方案考慮到了年級特點，但沒有考慮到性別的差異.

他們的抽樣調查不具有廣泛性和代表性.

抽樣方案1：隨機抽取該校七、八、九年級男、女生各20人的成績.

抽樣方案2：隨機抽取該校各年級學生（男、女生不限）共120人的成績.（答案不唯一.）

（2）平均數為

[4×30+3×45+2×30+1×1530+45+30+15=][2.75]（分）.

抽查的120人中，成績3分出現的次數最多，共出現45次，因此眾數是3分.

將這120人的得分從小到大排列，處在中間位置的兩個數都是3分，因此中位數是3分.

答：這組數據的平均數是2.75分，中位數是3分，眾數是3分.

【評析】通過考查評價抽樣方案樹立審辯式視域下的統計思想，通過考查設計抽樣方案培養創新視角下的統計意識.

2. 試題的綜合性

例20 （江蘇·鹽城卷）為了防控新冠疫情，某地區積極推廣疫苗接種工作，衛生防疫部門對該地區八周以來的相關數據進行收集整理，繪制得到圖15、表10.

根據統計表中的數據，建立以周次為橫坐標，接種人數為縱坐標的平面直角坐標系，并根據以上統計表中的數據描出對應的點，發現從第3周開始這些點大致分布在一條直線附近，現過其中兩點（3，12），（8，42）作一條直線（如圖16），該直線的函數表達式為[y=6x-6]，那么這條直線可近似反映該地區接種人數的變化趨勢.

試根據以上信息，解答下列問題：

（1）這八周中每周接種人數的平均數為? ? ?;該地區的總人口約為? ? ?.

（2）若從第9周開始，每周的接種人數仍符合上述變化趨勢.

① 估計第9周的接種人數約為? ? ?.

② 專家表示：疫苗接種率至少達60%，才能實現全民免疫.那么，從推廣疫苗接種工作開始，最早到第幾周，該地區可達到實現全民免疫的標準？

（3）實際上，受疫苗供應等客觀因素影響，從第9周開始接種人數將會逐周減少[a][a>0]萬人，為了盡快提高接種率，一旦周接種人數低于20萬人時，衛生防疫部門將會采取措施，使得之后每周的接種能力一直維持在20萬人.如果[a=1.8]，那么該地區的建議接種人群最早將于第幾周全部完成接種？

分析：（1）利用平均數的計算公式計算可得結論;用前8周已接種人數的和除以22.5%，可得結論.

（2）① 將[x=9]代入[y=6x-6]中，計算后可得結論.

② 計算出實現全民免疫所需的接種人數為[800×60%;] 設最早到第[x]周，該地區可達到實現全民免疫的標準，依題意列出不等式，通過計算可得結論.

（3）依題意計算出第9周的接種人數，進而計算出第[x]周的接種人數，根據題意列出不等式，解不等式得到從第21周開始接種人數低于20萬，再依據題意列出完成全部接種時，滿足的不等式即可得出結論.

【評析】此題考查了算術平均數、頻數、頻率、數據總數等統計知識，涉及一次函數、一元一次不等式組、分段函數等其他數學核心內容，試題來自身邊的素材“統計接種疫苗人數”，通過借助統計思想及結合統計知識進行分析推斷出今后接種疫苗工作的發展趨勢，具有現實意義，體現了數學來源于生活并應用于生活的基本理念.

在2021年全國各地的中考試題中，“抽樣與數據分析”部分考查的難度相對較小，但以實際生活為背景，“活而不難”的情境類試題仍屢見不鮮，一線教師要明確試題分析中的四個常見的考查“立足”點，還要注重解法分析中的三“從”. 今后在解決實際問題時，要注意引導學生樹立統計意識，運用統計思想，重視數據收集、數據整理、數據描述、數據分析的過程，培養學生解決問題的能力.

參考文獻：

[1]中華人民共和國教育部制定. 義務教育數學課程標準（2011年版）[M]. 北京：北京師范大學出版社，2012.

[2]周啟東，鄭艷. 2020年中考“抽樣與數據分析”專題解題分析[J]. 中國數學教育（初中版），2021（3）：18-25，31.