挖掘教材文本，有效設計“拓展延伸”，提升學生數學素養

張忠

摘 要：有效的數學課堂結構主要包括問題情境、建構活動、數學化認識、基礎訓練和拓展延伸五個部分。我們數學教學關注全體學生在“基礎知識、基本技能、基本思想、基本經驗”方面發展的前提下，還要精心設計“拓展延伸”教學內容，引導學生的思維活動，拓展他們的思維空間，進而提高他們的綜合數學素養。恰當、適度地拓展延伸教學內容，往往就來源于教材文本，本文結合相關案例從不同視角闡述對“拓展延伸”設計的認識。

關鍵詞：拓展延伸;挖掘教材;數學素養

“人人都能獲得良好的數學教育，不同的人在數學上得到不同的發展。”因此，數學教師應認真研讀《標準》和教材，明確每節課的教學目標，從中挖掘出相關素材進行有效設計、優化課堂教學結構。下面，筆者結合相關案例從不同視角闡述對“拓展延伸”設計的認識。

一、數學思想方法的橫向拓展

1.案例1

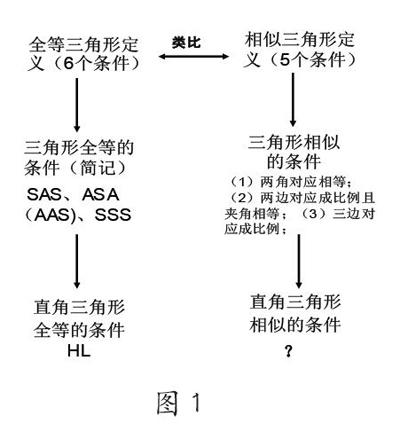
由于三角形全等是三角形相似的特殊情況，所以在設計蘇科版教材九年級下《6.4探索三角形相似的條件》教學時，我沒有完全按照教材的體系進行教學，而是把教學目標由“課時目標”調整為“單元目標”，即類比三角形全等的定義和判定方法的探索進程，將教材內容進行整合，在第一課時就先搭建起“探索三角形相似的條件”的框架，然后在后續的課上再對每一種判定方法進行推理說明、應用，從而使學生對本單元的研究與探索有一個整體的認識。于是，在第一節課我設計了三個問題讓學生思考或討論：

問題1.回憶相似三角形的定義。

問題2.回憶全等三角形的定義，并與相似三角形定義比較有何異同。

問題3.回憶全等三角形的判定方法，由此猜想兩個三角形相似需要具備哪些條件？

然后引導學生猜想并畫出三角形相似與全等之間的結構圖（如圖1）。

2.有效性分析

本案例運用類比的思想方法，很容易引導學生建構起上述的知識體系，同時能感悟到對于三角形全等或相似的判定，定義是最基本的方法，而從定義到一般的判定方法的猜想與探索就是一個條件弱化、減少的過程;而對于直角三角形全等的判定，不僅可用一般三角形全等的判定方法也有它自身的特殊方法;類似地，直角三角形相似的判定是否也有更簡單的方法呢？筆者留了一個問號，讓有興趣的同學在本單元的學習結束后繼續去猜想、探索，以此培養學生要注重新知識的探索方法與形成過程，而不是簡單的結果，這種通過數學思想方法的橫向拓展訓練，可最大化地提高課堂教學效益，引導學生進行有效的數學思考，開闊他們的數學視野。

二、數學知識結構的縱向拓展

1. 案例2

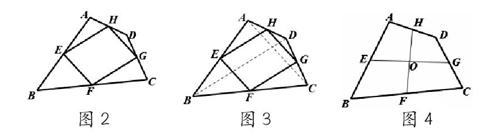
在四邊形的探索研究中，我們得到結論“依次連結一個任意四邊形各邊中點，所得到的四邊形一定是平行四邊形”，即：如圖2，四邊形ABCD中，點E、F、G、H分別為各邊的中點，則四邊形EFGH是平行四邊形。這里綜合地考察了“三角形中位線性質定理”和“平行四邊形的判定定理”。

圖中四邊形EFGH一般稱作“中點四邊形”，它的形狀只與四邊形ABCD的對角線AC、BD的數量、位置有關;同時，它的面積與四邊形ABCD的面積也有關系。因此，在上述基礎上，我們作如下的再探索和思考。

探索一：

如圖3，四邊形ABCD中，點E、F、G、H分別為各邊的中點，四邊形EFGH一般稱作“中點四邊形”。連結AC、BD，容易證明：中點四邊形EFGH一定是平行四邊形。

（1）如果改變原四邊形ABCD的形狀，那么中點四邊形EFGH的形狀也隨之改變，通過探索發現：

當四邊形ABCD的對角線滿足AC=BD時，四邊形EFGH是菱形;

當四邊形ABCD的對角線滿足? ? ? ? ?時，四邊形EFGH是矩形;

當四邊形ABCD的對角線滿足? ? ? ? ?時，四邊形EFGH是正方形;

（2）探索△AEH、△CFG與四邊形ABCD的面積之間的等量關系，請寫出你發現的結論并加以證明;

（3）如果四邊形ABCD的面積為2，那么中點四邊形EFGH的面積為多少？

探索二：

如圖4，在四邊形ABCD中，點E、F、G、H分別是AB、BC、CD、DE的中點，EG與FH相交于O點。

（1）猜想EG與FH有怎樣的關系？并證明你的結論。

（2）請添加一個條件? ? ? ? ? ? ? ?，使得EG與FH互相垂直。（3）若四邊形AEOH、BEOF、CFOG的面積分別為15、17、16，求四邊形DGOH的面積;若四邊形AEOH、四邊形BEOF、四邊形CFOG、四邊形DGOH的面積分別為S1、S2、S3、S4，利用（3）的計算結果;直接寫出S1、S2、S3、S4它們之間的關系。

2.有效性分析

本案例是對教材文本內容的再思考、再探索，深層次地進行了“挖掘”，并與相關問題進行了適當的聯系，是對數學知識結構的縱向拓展。這個問題有較強的探究性，思維要求較高，故對不同的學生應加以分層要求，可以放到課后讓學生思考、探究，甚至合作完成，這樣即有助于學生對“中點四邊形”的全面理解，起到舉一反三、觸類旁通的效果，又能引導學生形成動態、全面地思考認識問題的習慣，教師平時應該多引導學生多進行這樣的總結和反思，反思題目的條件與結論之間的關系及分析思路、結論是否能推廣，反思如何引導學生從中進行創造性思維的活動、多角度思考問題及多種方法解決問題，從而提高學生的思維能力及學習數學的興趣。

三、數學活動經驗的橫向拓展

1.案例3

在蘇科版數學八年級下冊我們學習了分式的基本性質： 分式的分子和分母都乘以（或除以）同一個不等于0的整式，分式的值不改變，即 =，=（其中B≠0，M為整式且M≠0）。

勤學善思的小明同學對此性質產生了疑問： 分式的分子和分母都加上（或減去）同一個不等于0的整式 ，分式的值會怎樣呢？即? = （其中B≠0，M為整式且M≠0）成立嗎？

我們先來解決一個身邊的問題：

一般地，在水中加入的糖越多，糖全部溶解后糖水就越甜。將A克白糖加水配制成B克糖水（B>A>0），此時糖水中的含糖量為;若再加入M克白糖（M >0），待全部溶解后糖水中的含糖量變為。根據生活經驗，我們可以得到一個不等式： < ，你能說明其中的道理嗎？

實際上， - = = ，因為B>A>0，M>0，則>0，即 <，由此可知，一般地 ≠（其中B≠0，M為整式且M≠0）。

2.有效性分析

上述案例是對分式性質的再思考，所產生的問題是對學生原有的數學知識、經驗的一個橫向拓展，部分學生很自然產生一個疑問。而問題的探索與解決，則先是在生活經驗的基礎上去思考，然后主要通過“作差”、分式的運算來比較分式值的大小，其中的“作差”、分式的運算是學生已有的數學活動經驗，這樣較直觀地用所學的知識解決了小明的疑問，從而對分式的性質有了更深的理解。這種有效性設計，就是讓學生感悟到數學的學習不能只停留在對教材的理解和掌握上，而應有更開闊的視野和認識。

利用上述結論，我們還可以解決下面的問題。

如圖5，矩形草坪的長為a米，寬為b米（a>b>0），沿草坪四周外圍有條寬為x米（x>0）的環行小路。

（1）草坪的寬與長的比值m=? ? ? ? ，外圍寬與長的比值n=? ? ? ? ? ?（用含有a、b、x的代數式表示）;

（2）請比較m與n的大小;

（3）圖中的兩個矩形相似嗎？為什么？

分析：（1）m=，n=;

（2）由上述材料可知：<即m < n;

（3）圖中兩個矩形不相似，理由：雖然這兩個矩形的4個角都對應相等（都是直角），但由<可知，它們的4條邊不對應成比例，所以它們不相似。

以上是從三個不同方面簡要地介紹了從教材文本中挖掘素材進行有效的拓展延伸設計，這些只是有效教學設計的一個環節。其實有效的課堂教學設計還有很多課題值得研究，我們數學教師要認真鉆研教材，創造性地運用教材，把握教材的編寫意圖及結構框架，讓教學設計逐漸完善、有效，讓學生的學習更加主動、富有個性化，學生的學習活動應是拓展延伸的集散地，這就要求我們在數學本質上聚焦教學活動[2]，從而實現人人都有不同的發展，最終會學數學，提高綜合數學素養。

參考文獻：

[1]中華人民共和國教育部.義務教育數學課程標準[S].北京師范大學出版社.2011

[2]卜以樓.生長數學：卜以樓初中數學教學主張[M] .西安：陜西師范大學出版社.2018.137