用心共情創優課
勞榮旦
摘?要:本文主要以活動課“探究四點共圓的條件”教學為例,以廣西特級教師戴啟猛的四度六步教學法的教學主張為主體框架進行設計,希望開展一節有趣,有深度的活動課,也讓本節課的各個環節都落實好,讓學生學有所獲。
關鍵詞:初中數學;四度六步教學法;探究四點共圓
魏書生老師的課堂講究少講多讀,精講才能讓學生記得住,多讀才可能提高學生閱讀的能力,近年中考的某些題型也重點考查了閱讀能力。六步教學法打破了傳統的單純傳授知識、填鴨式、滿堂講的課堂模式,有效解決了教學中教與學的關系中存在的問題,以學生為主體,把更多時間留給學生.
一、何為“四度六步”教學法
“四度六步”教學法,是指教師以追求 “四度” ,即有溫度、有梯度、有深度和有寬度。課堂為教學主張,依照 “溫故” ,即復習提問,溫故孕新, “引新”,即創設情境,引入課題,“探究”,即合作探究,活動領悟,“變式”,即師生互動,變式深化、“嘗試”,即嘗試練習,鞏固提高,、“提升”,即適時小結,興趣延伸等六個環節展開知識教學,此教學法的目標就是為了創造更優質生動的課堂,并且通過這六個環節,可以更扎實滲透教授內容.
二、教學過程精記
(一)溫故
問題1:在前面的學習中,我們學習了如何確定一個圓?
追問1:探究此結論的一般過程是什么?
追問2:經過一點A可以作多少個圓?
追問3:經過兩點A、B可以作多少個圓?
追問4:經過三點呢?
問題2:經過四個點呢?這四個點有什么位置關系?
追問:那不共線的有多少種情況?
師生活動:教師提出問題,學生思考并回答問題.
設計意圖:從經過一個點的圓、經過兩個點的圓、經過不共線的三個點的圓,再到經過任意三點都不共線的四個點的圓,從學生已有的學習經驗、學習方法出發,激發學生探索的動力、以及明確探索的方向和方法.
(二)引新
類比探究,引出課題,讓學生感知類比學習的應用.
探究:過任意四邊形的四個頂點能作一個圓嗎?動手試一試.
(給出三類四邊形讓學生畫,分別是矩形、對角互補的四邊形、對角不互補的四邊形)
問題:四邊形的哪些元素決定了過它的四個頂點可以作一個圓?請觀察猜想并通過測量驗證.
師生活動:教師給出幾個圖形,讓學生畫圖,學生類比作不共線三點的圓的方法獨立完成畫圖,然后觀察發現,得到猜想并測量驗證,學生在畫圖時出現可能的方法一般有兩種:
(1)作四(三)條邊的垂直平分線看是否交于一點,由圓的定義可以說明此方法可行;
(2)作出任意三點的圓,看第四個點是否在該圓上.
設計意圖:學生動手探究,自己獲得猜想,經歷知識的形成過程,引導學生從四邊形的邊或角等方面去猜想,進而探究.
(三)探究
問題:如何證明過對角互補的四邊形的四個頂點能作一個圓?
師生活動:教師提出問題,師生共同寫出已知、求證.
學生先獨立思考,然后再分組討論,提出想法嘗試回答.
追問1:已知任意不共線的三點一定能作一個圓,即證明四邊形的四個點共圓,就只需要證明第四個點是否在圓上即可,那如何證明第四點在這個圓上呢?
師生活動:學生可能嘗試證明這第四個點與圓心的距離等于半徑,但是這種方法是存在困難的.
追問2:假設點D不在過三點A,B,C的圓上,那點D與這個圓有怎樣的位置關系?
師生活動:師生一起分析點D在圓內的情況,利用圓的內接四邊形對角互補進行證明.
追問3:對于點D在圓外的情況,你能自己完成嗎?
設計意圖:讓學生在動手活動的過程中對反證法進行鞏固并感受到數學的嚴謹性,以及數學結論的確定性和證明的必要性,也培養了學生的推理能力.
(四)變式
變式:平面上四個點連成共底邊的兩個三角形,且兩三角形都在這條底邊的同側,若底邊的對角相等,請問:四點共圓嗎?
學生的回答是肯定的,此時再用幾何畫板對猜想進行驗證,讓學生初步明確該變式的結論后,師生共同寫出已知、求證,讓學生獨立嘗試推理論證.
設計意圖:變式題是鞏固反證法的應用,提升邏輯推理能力.
(五)嘗試
課堂練習:
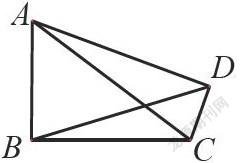
1、如圖,在四邊形ABCD中,∠ABC=∠ADC=90°,∠CAD=23°,則∠ABD的度數為?.
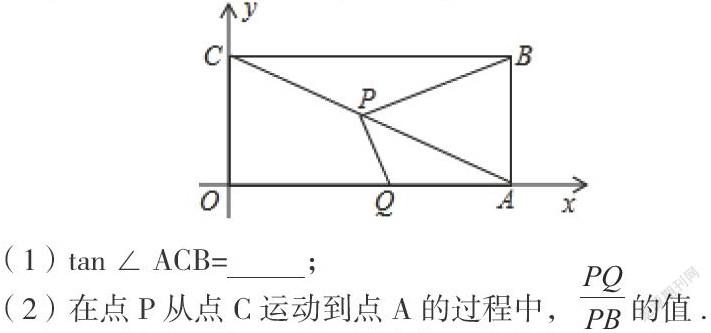
2、如圖,在平面直角坐標系中,已知矩形OABC的頂點A在x軸上,頂點C在y軸上,OA=8,OC=4,點P為對角線AC上一動點,過點P作PQ⊥PB,PQ交x軸于點Q.
(1)tan∠ACB=?;
(2)在點P從點C運動到點A的過程中,的值.
是否發生變化?如果變化,請求出其變化范圍;如果不變,請求出其值.
歸納:得到四點共圓可用于證明或求解角或線段的關系.
設計意圖:對新知的鞏固提升,練習2第(2)問可以用相似的知識解決,也可以證明四點共圓后,利用圓的性質解決.學生會感受到后者的方法較簡便.即體現了利用四點共圓的判定,將四邊形的問題轉化為圓的問題來解決的優勢.
(六)提升
教師與學生一起回顧本節課所學的主要內容,并回答以下問題:
(1)本節課你學到了什么知識?學到的知識能解決什么問題?
(2)回顧本節課的學習過程,你是怎么得到上述知識的?
設計意圖:通過課堂小結,讓學生總結提煉本節課學習的知識、技能以及研究方法,增強學生的數學學習能力.
三、教學反思
在傳授知識時,讓學生經歷知識的形成過程,有利于學生“懂數學”和“用數學”.在課堂中,盡量給學生表達自我的舞臺,特別是練習環節方面是比較放開給學生去表達的,目的就是為了提升學生的學習數學的自信心.本節課為活動課,但是在探究活動環節時沒有完全地放開給學生,給學生探究活動的時間還不夠充足,而我想到的解決方式是可以適當再減少練習,或者是在前面的引導環節中能夠更緊湊,語言更精煉些.
總之,為了創造更優質的課堂,我會繼續努力探索,學習一直在路上……
參考文獻:
[1]戴啟猛.基于初中數學 “四度六步”教學法的理論基礎與實踐架構[J].中小學課堂數學研究,2020(3).
[2]溫春紅、農學寧.緊扣核心知識,精準指導備考——以一節中考應用題復習專題研究課為例[J].廣西教育,2020(7).

