例談思維導圖在初中數學高效課堂中的應用

張錦理

【摘要】初中數學，對很多初中學子來說是一個難學的學科。這主要是因為初中數學的內容比較枯燥、抽象，題型更是千變萬化，靈活性較高。而初中階段，學生的抽象思維、邏輯思維都還沒得到很完整健全的發展。這就造成初中生的數學成績整體較差，學生望“數”生畏。因此，如何利用數學教學培養學生的思維能力，使課堂教學的效率最大化，是教師需要重點探索的問題。而思維導圖在初中課堂的應用，可以提高學生的學習興趣，發展學生的邏輯思維能力。研究思維導圖在初中數學課堂中的實踐應用，對于初中數學教學的改革與創新具有很重要的意義。

【關鍵詞】思維導圖;初中數學;課堂教學;實踐應用。

一、思維導圖提出

“思維導圖”是由英國著名的心理學家東尼·博贊最先提出并命名的。思維導圖是通過清晰的紋路和線條、有趣的圖形、豐富的色彩，來吸引人們的注意力，從而使人們對導圖里的圖案產生興趣，加深對知識的理解和記憶。思維導圖的本質是以立體的方式思考文本，即整體把握，又聯系局部，幫助學生更好地聯系新舊知識，加深對新知識的理解和記憶。

二、思維導圖應用于初中數學課堂的價值

思維導圖在初中數學課堂的應用，主要可以起到怎樣的作用呢？從學生層面上來看，主要體現在三個方面。一是思維導圖的形象生動性可以提高學生學習的積極性，活躍課堂氣氛;二是幫助學生構建數學思維結構;三是提高學生解決數學問題的能力。

從教師層面上來看，主要體現在四個方面。一是教師可以利用思維導圖優化知識結構，使教學更加嚴謹，提高學生的自學能力;二是教師可以利用思維導圖突出教學的重點和突破教學難點（如概念教學），提高學生自主認知能力和辨析能力;三是教師可以利用思維導圖對知識點進行整合和延伸，提高學生的總結能力和知識拓展能力;四是教師以思維導圖為媒介，加深師生間的交流，幫助學生提高解決問題能力，從而提高課堂教學的效率。

三、對思維導圖在初中課堂中應用的困惑

“思維導圖在初中數學課堂教學的實踐研究”，在科組決定要研究這個課題時，筆者對思維導圖的了解并不深入。在筆者的求學生涯中，也有用過思維導圖幫助梳理知識點和加深對所學內容的理解與記憶，但是這多半用于語文、政治等文科科目的學習，在像數學這類理科科目中并沒有使用思維導圖去解題的習慣，最多在章末復習時，把本章的知識框架利用思維導圖梳理出來，以幫助了解知識之間的聯系，同時加深對知識點的記憶和理解。但是在數學的新課或習題課，并不會使用思維導圖去展開。難道說，我們只能傳統地將思維導圖應用到數學復習課的課型里嗎？那么新授課呢？習題課呢？又該如何用思維導圖去展開新課的教學呢？

四、高效地將思維導圖應用于數學的新授課

在和科組成員的交流討論下，筆者借鑒其他幾位課題組老師的實施方案，再加入自身對思維導圖的理解，我們一致認為除了復習課外，思維導圖也可以應用于新授課和習題課。數學是一門很講究思維和方法的學科，學生在探究新課知識點和做習題時，可以應用思維導圖去做分析和推導，以找到解題的思路和突破口。在教學中，我們可以引導學生應用色彩豐富的思維導圖去分析、研究，從知識點的研究背景和題干條件出發，結合所學知識去推導初步的結論，接著在從初步結論出發，繼續得出二次結論，層層遞進，最后綜合觀點，得到所要得出的結論和答案。

根據筆者的構想，下面以“利用‘邊邊邊判定三角形全等”一課為例，將思維導圖應用于新授課的課堂教學中。以下是筆者的教學設計和課堂實錄：《利用“邊邊邊”判定三角形全等》是新北師大版七年級下冊第四章第三節的內容，分為三個課時，這節課設計的是第一課時。探究三角形全等的條件是在學生初一階段學完三角形的相關概念基礎上對三角形全等的進一步深入學習，《探究三角形全等的條件——邊邊邊公理》這是這一章的重點內容，起到承上啟下的作用，所以學好這節課是至關重要的。判定三角形全等是初中階段很重要的一種幾何證明題，它的難點在于如何很清晰準確的找出判定兩個三角形全等的邊、角有關的條件，題目的意圖是利用哪一種判定方法去證明兩個三角形全等——三角形全等的判定定理。為了讓學生做這一類題目的思路更清晰，答題更準確、快速，筆者覺得這個難點的突破口是我們在講課的時候可以加入思維導圖去分析解題思路。

在和學生一起探究了判定三角形全等的條件需要幾個，并最終得出了“邊邊邊”公理之后，就開始應用這個定理。如何用思維導圖去分析做題的思路呢？筆者用以下的例題為大家說明：

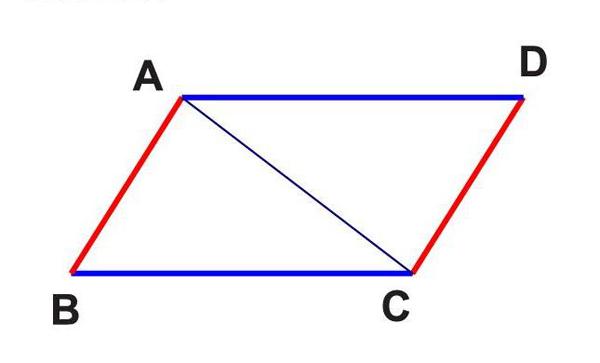
例1：如圖，當 AB=CD，BC=DA時，圖中的△ABC與△CDA是否全等？并說明理由。

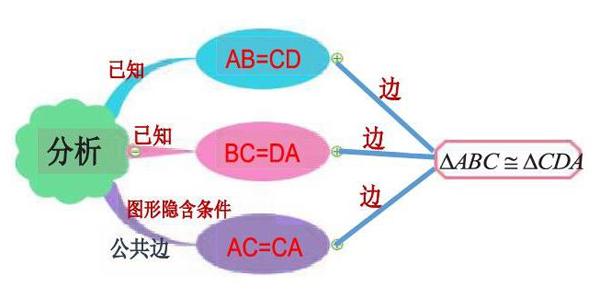
師：同學們，要判斷這兩個三角形全等，我們得先從題目和圖形出發，找出判定兩個三角形全等的邊、角有關的條件。下面我們一起利用思維導圖來分析。

接下來，筆者讓學生Z根據思維導圖的分析，上臺板演這題的詳細解答過程，其解答大致如下：

解：▲ABC≌▲CDA，理由如下：

因為AB=CD，BC=DA，AC=CA

所以▲ABC≌▲CDA

學生Z的解答雖然格式略顯粗糙，但基本已是正解，筆者肯定了他的解答，并以他的解答為基礎，跟學生強調做這類證明題的基本格式如下：

解：▲ABC≌▲CDA，理由如下：

在三角形▲ABC與▲CDA中：

∵ AB=CD（已知）

BC=DA（已知）

AC=CA（公共邊）

∴▲ABC≌▲CDA（SSS）

這就是將上面思維導圖中的枝干也加進去，學生很快就能理解以上思維導圖所傳遞的所有信息，環環相扣，互為因果，印象深刻。學生也能夠很快地掌握解題方法和格式，不易出錯。利用思維導圖分析證明的思路，學生就不會再出現一看到證明題就大腦一片空白，找不到思路的情況。

然后，筆者布置了對應的練習題，讓學生自己試著利用思維導圖去分析題目，并解答。題目如下：

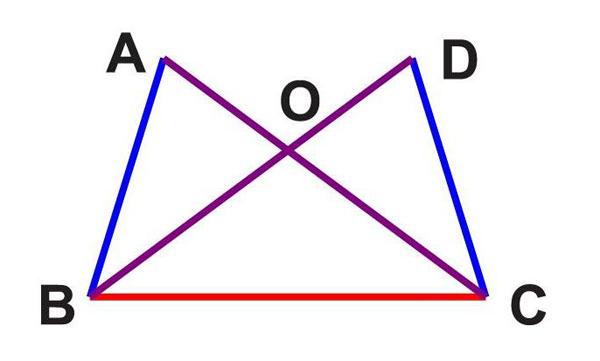
已知：AC、BD相交于點O，且AB=DC，AC=DB，那么△ABC全等于△DCB嗎？∠A=∠D嗎？為什么？

在學生做完之后，筆者展示了每個小組學生代表的解答成果，這里筆者向大家展示下J同學的分析和解答過程，如下圖：

從J同學的分析和解答來看，他十分高效地運用了思維導圖分析去題目傳達的信息，解題思路清晰，解答到位。可見，思維導圖的運用，提高是學生的解題效率，同時也提高了課堂教學的質量，活躍了課堂的氛圍。

這節課的最后，筆者用思維導圖幫助學生總結了這節新課的知識點，并啟發學生下節課的學習內容。

整一節課，思維導圖都是絕對的主角。學生在老師的演示下學習到我們可以用思維導圖去分析題目，揭開題目神秘的面紗，豁然開朗。它提高了學生學習新課內容的興趣和分析數學問題的能力。學生在老師的指導下，用彩色的筆，畫出一個個色彩鮮明、脈絡清晰的屬于自己的思維導圖，加強師生的交流，以及學生對題目的深入理解和動手能力。最后筆者以思維導圖小結課堂學到的知識點，并提出困惑，啟發學生下節課的知識點，提高學生學習下節課的積極性，優化整體的知識結構。

五、思維導圖在初中數學習題課中的應用

應用題是初中學生們最害怕的題型之一，因為數學中的應用題一般在最后兩道，綜合性比較強，一般設置在考試的最后幾道題里面。考試的應用題往往令許多學生摸不著所考的知識點，無從下手，沒有思路。而思維導圖可以幫助學生理清解題的思路，剝絲抽繭，提取題干中的主要信息，去除其次要信息，幫助學生找到解題切入點。以一道習題課的應用題為例，具體如下：小明爸爸騎著摩托車帶著小明在公路上勻速行駛，下圖是小明每隔1小時看到的里程情況.你能確定小明在12：00時看到的里程碑上的數嗎？

12：00 里程碑上是一個兩位數，它的兩個數字之和為7。

13：00 里程碑上的數字十位與個位數字與12：00時所看到的正好顛倒了。

14：00 里程碑上的數字比12：00時看到的兩位數中間多了個0。

【分析】設小明在12：00時看到的兩位數的十位數字為x，個位數字為y。

等量關系：（1）數字和為7：x+y=7

（2）路程差相等

（10y+x）-（10x+y）= （100x+y）-（10y+x）。

用思維導圖一分析，這道比較難理解的題目的思路漸漸就十分清晰明了，答案也呼之欲出。在分析的同時也提高學生的邏輯思維能力。

之后，筆者將這一方法進行拓展延伸，引導學生將思維導圖應用到其他類型題目的解題分析中去，對“思維導圖”分析法解題進行深入推廣。學生做題的效率得到了很大的提高。同時，也讓學生意識到思維導圖模式是一種解決數學問題的高效思維模式，它可以將復雜的數學問題變得簡單、具體，幫助學生理解題目意思，并找到解題的思路。

六、結束語

筆者認為，用思維導圖分析數學問題是一種效率好、準確性高的解題方法。從學生層面來說，思維導圖可以幫助學生克服了對數學解答題的畏懼心理，激發學生學習數學的興趣、提高學生的解題能力，培養學生梳理知識點和提取題目要點的實踐動手能力。從教師層面來說，思維導圖增加了師生的課堂交流，讓學生變成了課堂的主人，去圈畫、描繪一幅幅生動而又不失色彩的導圖，優化了教師的教學知識結構，大大地提高了初中數學課堂教學的效率。希望更多的初中數學教學工作者能將思維導圖融入自己課堂教學中去，豐富課堂教學的色彩和內容。

盡管思維導圖在初中數學課堂中的應用還不是很廣泛，但這也不能否認它在初中課堂教學中的價值。為此，以上我們探究了思維導圖在初中數學新授課和習題課課堂中的高效應用，接下來研究應用思維導圖幫助學生進行初中數學自主預習是我們努力的方向。

[本文系河源市2018年中小學（幼兒園）教學研究課題“思維導圖在初中數學課堂教學的實踐研究”（課題編號：hy18062）的階段性成果]

參考文獻：

[1]鐘進均.基于信息不對稱理論的高中“說數學”[J].數學通訊，2016（11）.

[2]戚美群.基于思維導圖的初中數學高效課堂的構建[J].教育咨詢·教育科研，2020（02）.

[3]王偉基.淺談思維導圖在初中數學中的應用[J].教學·信息·課程教育研究，2019（39）.

[4]馬憲蓉.思維導圖在數學課堂教學中的應用[J].報刊薈萃（上），2018（05）.

[5張艷.例談思維導圖在小學數學教學中的應用[J].學術研究，2014（12）.

[6]甄玉蓮.思維導圖模式在初中數學課堂中的運用[M].中學教學參考·理科版，2016（06）.