運(yùn)用轉(zhuǎn)化思想提升學(xué)生的數(shù)學(xué)核心素養(yǎng)

周月容

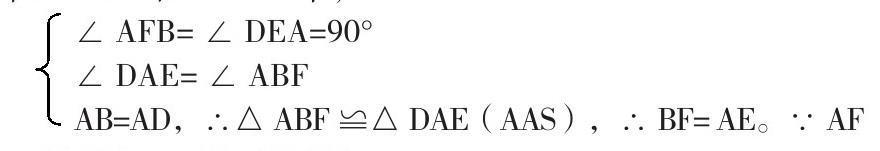
【摘要】核心素養(yǎng)是指學(xué)生應(yīng)具備的適應(yīng)終身發(fā)展和社會發(fā)展需要的必備品格和關(guān)鍵能力。數(shù)學(xué)思想是對數(shù)學(xué)知識的本質(zhì)認(rèn)識和數(shù)學(xué)規(guī)律的理性認(rèn)識，是建立數(shù)學(xué)和用數(shù)學(xué)解決問題的指導(dǎo)思想。在教學(xué)中，引導(dǎo)學(xué)生運(yùn)用數(shù)學(xué)思想解決和處理數(shù)學(xué)問題，對于提升學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)意義重大。其中，轉(zhuǎn)化思想引領(lǐng)學(xué)生在解決有關(guān)數(shù)學(xué)問題時對數(shù)學(xué)命題進(jìn)行等價轉(zhuǎn)化或非等價轉(zhuǎn)化，使問題在轉(zhuǎn)化中得到解決。

【關(guān)鍵詞】數(shù)學(xué)核心素養(yǎng);轉(zhuǎn)化思想;線段的和差關(guān)系

數(shù)學(xué)思想是對數(shù)學(xué)知識的本質(zhì)認(rèn)識和數(shù)學(xué)規(guī)律的理性認(rèn)識，是從某些具體的數(shù)學(xué)內(nèi)容和對數(shù)學(xué)的認(rèn)識過程中提煉上升的數(shù)學(xué)觀點(diǎn)。中學(xué)階段的數(shù)學(xué)思想主要有：數(shù)形結(jié)合思想、函數(shù)和方程思想、分類討論思想、集合對應(yīng)思想、轉(zhuǎn)化思想，化歸思想以及邏輯思想等。在數(shù)學(xué)教學(xué)中，引導(dǎo)學(xué)生運(yùn)用數(shù)學(xué)思想解決和處理數(shù)學(xué)問題，對于提升學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)意義重大。其中，轉(zhuǎn)化思想是最常見的數(shù)學(xué)思想方法，其最基本思路是在解決有關(guān)數(shù)學(xué)問題時對數(shù)學(xué)命題進(jìn)行等價轉(zhuǎn)化或非等價轉(zhuǎn)化，使問題在轉(zhuǎn)化中得到解決。現(xiàn)以“線段的和差關(guān)系探究”教學(xué)中的一道習(xí)題的教學(xué)為例，對如何運(yùn)用轉(zhuǎn)化思想引導(dǎo)學(xué)生掌握知識，培養(yǎng)學(xué)生良好數(shù)學(xué)素養(yǎng)進(jìn)行論述。

在復(fù)雜多變的幾何圖形中，探究線段的和差關(guān)系的“變”與“不變”是數(shù)學(xué)解答題中最富有活力的一類題型。這種題型通常是已知在一個較為簡單（或特殊）情況下，求證3條線段之間的和、差關(guān)系。學(xué)生通過思考與探索比較容易得證，然后再設(shè)計一個題設(shè)、圖形變化的數(shù)學(xué)環(huán)境，進(jìn)一步探索原結(jié)論是否成立。在此過程中，讓學(xué)生逐步形成猜想、推理論證、應(yīng)用解決問題的能力等良好的數(shù)學(xué)學(xué)科素養(yǎng)。下面以八年級下冊第62頁習(xí)題18.2第15題為例。

四邊形ABCD是正方形，G是線段BC上的任意一點(diǎn)，DE ⊥AG于點(diǎn)E，BF∥ DE，且交AG于點(diǎn)F，求證：AF - BF=EF。（圖1）

思路： 筆者引導(dǎo)學(xué)生觀察圖形：由圖形可知AF - AE=EF，而題目要求證AF - BF=EF，即只需要證明AE=BF，也就是只要△ABF≌△ADE，問題即可得證。也就是將不在同一條直線的兩條線段轉(zhuǎn)化到同一直線上，這就是運(yùn)用了數(shù)學(xué)的轉(zhuǎn)化思想。線段的和差問題的探究常常借助于全等三角形的對應(yīng)邊相等， 將不在同一條直線的兩條線段轉(zhuǎn)化到同一直線上。

證明：∵DE⊥AG且DE∥BF，

∴BF⊥AG，

∴∠AFB=∠DEA=90°。在正方形ABCD中，AB=AD，∠BAD=90°，即∠BAF+∠DAE=90°，在Rt△ABF中，∠BAF+∠ABF=90°，∴∠DAE=∠ABF。在△ABF和△DAE中，

∠AFB=∠DEA=90°

∠DAE=∠ABF

AB=AD，∴△ABF≌△DAE（AAS），∴BF= AE。∵AF - AE=EF，∴AF - BF=EF。

本引例的解答過程主要借助于全等三角形的對應(yīng)邊相等，將不在同一條直線的兩條線段轉(zhuǎn)化到同一直線上，學(xué)生在探究的過程中運(yùn)用了轉(zhuǎn)化思想，將證線段和差轉(zhuǎn)化為證三角形全等。在解決這類問題的過程中，筆者注重引導(dǎo)學(xué)生體會知識的形成過程，培養(yǎng)學(xué)生解決問題的能力，提升學(xué)生數(shù)學(xué)的核心素養(yǎng)。

接著，筆者對題目的已知條件進(jìn)行改變。變形題：“點(diǎn)G是線段BC上的任意一點(diǎn)”改為“點(diǎn)G是線段CB延長線上一點(diǎn)”，其它條件不變，請在圖2中畫出圖形。猜想：線段EF、 BF、 AF之間的關(guān)系，并說明理由。

引導(dǎo)分析：

師：點(diǎn)G的位置變了，圖形也跟著變了，大家能畫出圖形嗎？（學(xué)生試畫）師：你覺得AF - BF還等于EF嗎？生：不會（觀察圖形可得到）。師：那可能會有怎樣的關(guān)系呢？師：猜想它們可能存在的關(guān)系？生：EF=AF+BF。師：仿照引例的思路，本題能否也借助證兩個三角形全等得出線段相等？還是△ABF和△DAE全等嗎？生：是的。師：∠BAF+∠DAE還等于90°嗎？角的位置變化了沒有？生：角的位置變化了，但是∠BAF+∠DAE還是等于90°。

至此，老師可要求學(xué)生仿照引例的方法，獨(dú)立完成證明過程。

本題首先提供圖1的位置情況下三條線段AF、 BF、 EF滿足的數(shù)量關(guān)系，并且給出了結(jié)論成立的邏輯推理過程，然后改變G點(diǎn)的位置，使問題中的幾何元素之間的相對位置發(fā)生變化，進(jìn)一步探究結(jié)論的“變”與“不變”，事實(shí)上也檢測了學(xué)生的類比猜想的推理能力。要驗證猜想的正確與否，就必須抓住問題證明過程中的關(guān)鍵——運(yùn)用轉(zhuǎn)化思想把證線段的和、差關(guān)系轉(zhuǎn)化為證明△ABF≌△DAE。

下面，用上面的方法再引導(dǎo)學(xué)生進(jìn)行此類型題的探究。

例：正方形ABCD中，∠MAN=45°，∠MAN繞著點(diǎn)A順時針旋轉(zhuǎn)，它的兩邊分別交CB，DC（或它們的延長線）于點(diǎn)M、N;當(dāng)∠MAN繞點(diǎn)A旋轉(zhuǎn)到BM=DN時，如圖1，易證BM+DN=MN。

（1）當(dāng)∠MAN繞點(diǎn)A旋轉(zhuǎn)到BM≠DN時，如圖2，線段BM，DN和MN之間有怎樣的數(shù)量關(guān)系？寫出猜想，并加以證明。

（2）當(dāng)∠MAN繞著點(diǎn)A順時針旋轉(zhuǎn)到如圖3的位置時，線段BM，DN和MN之間又有怎樣的數(shù)量關(guān)系？請直接寫出你的猜想。

小題（1）思路分析：觀察圖形，可以猜想BM+DN=MN。由于線段BM、DN不在同一直線上，可以考慮將它們轉(zhuǎn)移在同一直線上（線段DN轉(zhuǎn)移到線段BM所在的直線或是線段BM轉(zhuǎn)移到線段DN所在的直線）。在這里，將線段DN轉(zhuǎn)移到線段BM所在的直線的方法來分析（另一轉(zhuǎn)移法讓學(xué)生課后完成）。證明過程略。

小題（2）思路分析：觀察圖形，可以猜想：DN–BM=MN。仿照（1）小題在線段CB的延長線上取BF=DN，易證△ABF≌△ADN（SAS），所以BF=DN;AF=AN;∠BAF =∠DAM ;由于BF-BM=MF，那么只需證明MF=MN，即證明△AMF≌△AMN;跟小題（1）有變化的是證明全等的角關(guān)系變化了，因為∠MAN=45°，即∠BAM+∠BAN=45°①，由正方形的性質(zhì)知∠DAN+∠BAN=90°②，②-①得： ∠DAN -∠BAM=45°，所以∠BAF -∠BAM=45°（等量代換），即∠FAM=45°，所以∠FAM=∠NAM，易得△AMF≌△AMN，所以MF=MN，由等量代換得DN – BM=MN，結(jié)論得證。證明過程略。

課堂反思：解答本題的關(guān)鍵是構(gòu)造全等三角形，運(yùn)用轉(zhuǎn)化思想將線段DN轉(zhuǎn)移到線段BM所在的直線上，同時為下面要證△AMF≌△AMN創(chuàng)造條件。

事實(shí)證明，在教學(xué)過程中，引導(dǎo)學(xué)生重視數(shù)學(xué)思想的滲透，可以深化學(xué)生對基礎(chǔ)知識的理解，進(jìn)一步完善學(xué)生的認(rèn)知結(jié)構(gòu)，優(yōu)化學(xué)生思維品質(zhì)，提高學(xué)生認(rèn)識問題，解決問題的能力，提升學(xué)生的數(shù)學(xué)素養(yǎng)。

總之，數(shù)學(xué)學(xué)習(xí)過程是一個數(shù)學(xué)認(rèn)知結(jié)構(gòu)的發(fā)展變化過程，數(shù)學(xué)思想不僅提供思維策略，而且提供實(shí)施目標(biāo)的具體手段。教學(xué)時，積極進(jìn)行數(shù)學(xué)思想方法的滲透，將極大地促進(jìn)學(xué)生的數(shù)學(xué)學(xué)科核心素養(yǎng)的發(fā)展與提升。

參考文獻(xiàn)：

[1]王鋒 .一類變化圖形中線段和差關(guān)系的探究[J].試題與研究：中考版， 2011.

[2] 肖德好.全品大講堂[M].北京：開明出版社，2014.