挖掘習題價值 促進思維發展

沈良國

摘 要：教材是編者結合學生的思維發展特點與數學知識的規律經過仔細推敲、反復修改編定的，因此教材習題是最佳的練習資源。教師在備課時，鉆研各類練習題的配備情況是十分重要的。教師要充分挖掘習題的內涵，透析習題的設計意圖，并巧妙地結合學生的實際學情進行靈活運用。文章就如何挖掘教材的習題價值，從而有效促進學生思維發展進行了具體的闡述。

關鍵詞：習題價值;思維發展;數學課堂

中圖分類號：G623.5 文獻標識碼：A 收稿日期：2019-06-25 文章編號：1674-120X（2019）33-0085-02

一、挖掘習題本質，培養學生思維的縝密性

課堂練習是一種有計劃、有指導的教學活動，要通過有針對性的習題更好地鞏固學生所學的新知。因此，在設計習題時，必須要緊扣教學目標，每一道習題的練習意義都要明確，既要明確怎樣通過習題練習促進學生深化理解、掌握技能與發展能力，更要揭示習題本質。

例如，在教學蘇教版四年級下冊“乘法”一課時，教材第6頁編排了這樣的一道習題，就是讓學生在□里填上合適的數字，促使等式成立，即□□×□□=1600，□□×□□=2400。直覺思維促使學生很快根據乘法口訣表而想到“兩個整十數相乘”的想法，有的學生說：“20×80=1600。”有的學生說：“40×40=1600。”有的學生說：“30×80=2400。”有的學生說：“40×60=2400。”顯然，這道題兩個等式均是兩位數乘兩位數而積為四位整百數，學生的思維也僅僅局限于一種簡單式的條件反射。因而教師要揭示習題的本質，促使學生進行縝密性思考。教師要適時根據學生的思路進行引導：“這幾種想法的共同點是兩個乘數都是整十數，那么還能不能有不一樣的填法？”于是將學生的思維推向了深度，有的學生馬上反應過來：“可以將1600寫成16×100，但100是三位數，所以可以將16乘以2變成32，而100除以2變成50，那么這道算式還可以寫成32×50=1600。”對于這樣的思路，教師要進行即時性的贊賞評價，以進一步喚醒學生的思維。很快，一石激起了千層浪，有的學生說道：“可以將16乘以4，100除以4，所以也可以寫成64×25=1600。”有的學生這樣想：“我們同樣也可以將2400分成24×100，然而通過24分別進行擴大，將100分別進行縮小，所以同樣也可以得出這樣的算式：32×75=2400 ，48×50 =2400，96×25=2400。”這位學生一下子將所有的答案都說了出來。顯然，在教師的不斷追問與啟發下，學生的思維逐漸地從直覺性走向了縝密性。因此，教材中的習題是死的，而習題背后隱含的數學思想、數學方法與思維方法卻是深刻而鮮活的。教師要充分揭示習題的本質特點，從而有效地培養學生的縝密思維。

二、挖掘習題價值，培養學生思維的深刻性

大部分教師對于教材習題的使用缺乏深究意識，更多的聚焦點就是讓學生動手做一做，做完之后也只停留在答案的校對上。顯然，這樣的做法就無法觸及教材習題背后真正的教學價值，而對于學生思維深刻性的培養就難以得到落實。教師應致力于對教材習題價值進行深度開發，并借助教材習題，以一題而觸及一類問題，讓學生進行觸類旁通，這不但能促使學生有效地鞏固新知，更能培養學生思維的深刻性。

例如，筆者聽過一位教師執教的人教版五年級“長、正方體體積練習課”一課，這位教師整節課通過對教材中的一道習題進行充分的挖掘，并二度開發其習題背后的價值，從而有效地促進學生思維深刻性發展。教材練習八的第2題（如圖1），乍一看文字信息，這道題并不難。有的學生由于定勢思維的負干擾，通常能想到的就是用包裝盒的容積和玻璃器皿的體積做比較，如果玻璃器皿的體積比包裝盒長方體的容積小，就可以裝得下。看似順理成章，解題思路毫無破綻，如果只是以題講題，顯然這道題很快就過了。然而，在實際生活中，這種思維定式會導致學生思考問題的片面性。

正是基于這樣的認識，這位教師對這道教材中的習題進行了充分的開發與利用。在課堂教學中，教師將本題創編成了三道不同思維層次的題目。

先是出示基礎題（如圖2），題目出示之后，大部分學生直接認定可以裝下，但也有個別學生表示不解。教師及時地發覺了疑問，有位學生說道：“玻璃器皿的體積是比包裝盒的容積小，但也有可能人家玻璃器皿的長特別長，而寬特別窄，那么就不可能裝得下。”這個想法激起了全班學生火熱思考，大家紛紛贊同這位學生的看法。于是學生在一次次的舉例中達成了共識：要判斷到底能不能裝得下，不能單單只考慮它們的體積，而必須要考慮它們各自的長、寬、高。只有包裝盒的長、寬、高都比玻璃器皿的長、寬、高都大的前提下，才可以裝得下。

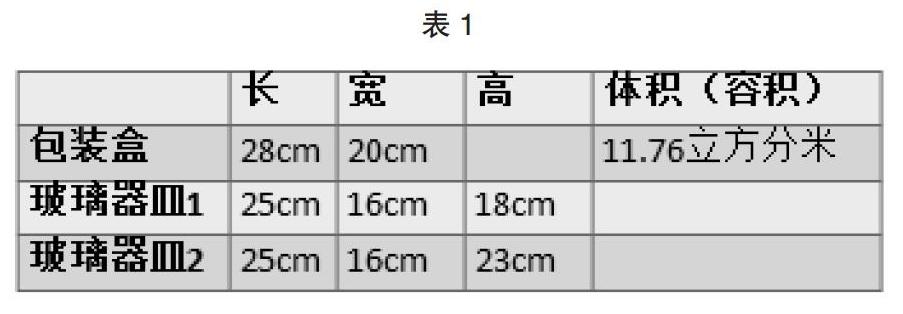
接著教師出示了對比題目，也就是教材中的原題。為了便于學生比較，教師引導學生把題目中的信息整理成一個表格。至此，學生不再急著計算玻璃器皿的體積，說明其思維的發展得到了有效提升，考慮問題更加全面了。為了進一培養學生思維的深刻性，這位教師又將這個玻璃器皿的高更改為23厘米，而其他信息都不變（如表1）。通過對比，學生馬上發現第二玻璃器皿的高比包裝盒的高要高，因而是裝不下的。最終學生通過思辨歸納得出結論：要判斷包裝盒能不能裝得下，有兩個層次，一是如果包裝盒的容積比長方體物體的體積小，那一定裝不下;二是如果包裝盒的容積比長方體物體的體積大，也未必裝得下，必須要考慮它們的長、寬、高。只有保證長寬高都大的前提下才裝得下。

此外，教師還設計了這樣一道拓展題：“有這樣一個包裝盒，從里面量長28cm，寬20cm，它的容積是9.52立方分米。而有一個玻璃器皿，它的長、寬和高分別是25cm、16cm和18cm，這個包裝盒能裝得下嗎？”教師同樣讓學生將題目中的信息整理成以下表格（如表2）。學生有兩種意見，一是有的學生認為雖然包裝盒的長和寬大于玻璃器皿的長和寬，而包裝盒的高卻比玻璃器皿的高矮，所以裝不下;二是有的學生認為可以裝得下，做法就是將玻璃器皿的寬和高轉換擺放的位置即可。然而教師沒有就此止步，而是引導學生繼續進行歸納發現：要判斷包裝盒能否裝得下，可以分別將玻璃器皿和包裝盒長、寬、高三組數據分別從大到小進行排列，并進行一一對應比較。如果玻璃器皿的長、寬、高的數據都比較小，則包裝盒一定能裝得下，反之則裝不下。

三、挖掘習題內涵，培養學生思維的靈活性

在實際教學中，大部分教師只重視例題的教學，對教材習題卻不屑于深究，如果缺少對習題的深度挖掘，必然會弱化教材習題的價值。作為教師，要充分挖掘教材習題自身的內涵價值。

例如，在教學“圓”的面積與周長之后，教材在練習十五第10題安排這樣的一道題（如圖3），題目要求學生算一個不規則圖形的周長。顯然，教材編者的意圖是要讓學生不但鞏固前面所學的圓周長的知識，而且是要滲透轉化數學思想的方法。基于這樣的認識，為了進一步挖掘習題內涵，筆者對這道教材習題進行了改動（如圖4），其目的一是為了讓枯燥的數學知識進行生動化的表達，“圓”宛如一個句號，出示改編后的圖形，則仿佛又是一個逗號;二是原題中是要求算出周長，而改編后則不但要求周長，還要求出面積，充分利用資源，豐富了習題的內涵。這樣的改編，讓學生在有趣的習題下進行多樣化算法的探索，不但能讓學生直觀理解各種算法的依據，而且有效地發展了學生思維的靈活性。

四、結語

綜上所述，教師應認識到習題對學生數學學習的重要價值，需利用現有的教材資源，充分挖掘教材習題價值，不斷培養學生的數學思維，進而有效提升學生的數學素養。

參考文獻：

[1]王 坤.運算律教學，不能止步于簡便運算——小學階段運算律的教學現狀、內涵及教學策略[J].小學數學教育，2018（12）：18-19.

[2]陳先波.關于學生數學差異性作業的應用[J].考試周刊，2012（34）：61-62.