注重思維訓練 促進分層教學
湯雙


[摘? 要] 分層走班制教學模式下如何培養C層(優秀)、D層(更優秀)學生的數學思維能力,挖掘潛力,關鍵是教學策略的選擇. 本文從課本一道引題入手,深入淺出地描述了“自主思考,重點展開,分步推進”策略在數學教學中的運用.
[關鍵詞] 數學教學;數學思維;分層教學;教學策略
2015年,筆者所在的學校積極響應《國家中長期教育改革和發展規劃綱要(2010-2020年)》中提出的注重因材施教的教育方針,結合學校實際,率先進行了基礎教育前瞻性教學改革,開展分層走班制教學活動,力求每位學生在最適合自己的環境中獲得基礎性學力、發展性學力、創造性學力的最佳發展.
本文以新人教版七年級下冊課本第65頁“平面直角坐標系”中一道練習題為引,簡述開展分層走班制教學模式后,筆者對C層(優秀)、D層(更優秀)學生數學思維能力培養的教學策略.
教學案例
原題:如圖1,甲處表示2街與5巷的十字路口,乙處表示5街與2巷的十字路口. 如果用(2,5)表示甲處的位置,那么“(2,5)→(3,5)→(4,5)→(5,5)→(5,4)→(5,3)→(5,2)”表示從甲處到乙處的一種路線. 請你用這種形式寫出幾種從甲處到乙處的路線.
課例解讀:著名的數學大師G·波利亞在探討教學論時曾經說過:“學習動機的形成有各種各樣的原因,其中最重要的是學生‘在學習中尋得快樂.”本題難度低、易理解、發散性強,多數學生能結合圖形找到路線,并通過有序數對將路線描述出來. 在解題過程中,每個層次的學生都享受到成功的快樂,激發出他們研究知識內在聯系的欲望.
教學變題
師:如果將引題變為:如圖1,若行走路線只能沿線向下和向右運動,則從甲處到乙處有多少種不同的路線?
師:(C層、D層學生)先獨立思考2分鐘,再以小組為單位,合作完成解答過程.
生1:我們組把滿足條件的路線一條條數出來,一共找出18條.
師:這種方法在數學中稱為“枚舉法”或“窮舉法”.
生2:我們組用的也是枚舉法,但是我們一共數出20條路線.
師:是嗎?兩個小組都用了枚舉法,結果卻不一樣. 這是什么原因?
生3:因為枚舉法適用于簡單問題的求解.
師:很好!本題還有其他解法嗎?
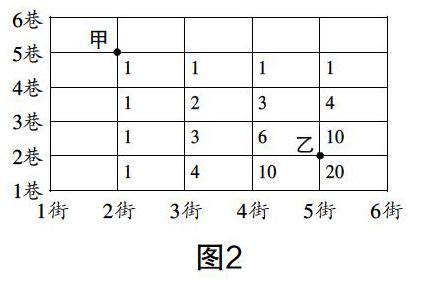
生4:首先,我找出經過每個點的路線,那么能從甲處到乙處的所有路線就是直接到達乙處的各點路線數之和. 詳細解法如圖2.
師:思考:在這個過程中,解題的關鍵是什么?
生4:確定能直接從甲處到乙處的點.
師:你的回答真棒!
課例解讀:著名的數學大師G·波利亞說:學東西最好的途徑是親自發現它,也就是說最富有成效的學習是學生自己去探索、發現.
變題的起點提高,需要團隊合作,思維的火花在合作與碰撞間綻放. 在學生討論出結果后,教師“畫龍點睛”,將學生的回答升華到理論層次,完成新知建構. 這種“自主思考,重點展開,分步推進”的策略成功引領學生在組內、組間開展思考、探究活動,讓每個人的注意力都集中在解題中,深刻體驗思維結晶.
教學拓展
分層教學的目的是滿足不同層次學生的學習需求,讓每個層次的孩子“吃飽”“吃好”,最終實現學生的學力提升. 面對C層、D層的學生,教學中,更需要我們精準備課,甄選題目,充分挖掘孩子的學習潛力.
師:如果將引題中“街與巷”的范圍擴大,你能找出每列每個節點處滿足條件的路線數的規律嗎?(要求:C層選做,D層必做)
生5:我們發現,2街一列相鄰兩個節點間路線都是1,3街越往下走,相鄰節點處路線依次增加1,4街越往下走,相鄰節點處路線依次增加2,3,4,…5街越往下走,相鄰節點處路線依次增加3,6,10,…
師:如果到第n行,各街節點處滿足條件的路線分別有多少條?
(大家各自思考1分鐘,然后小組討論)
生7:3街第n行節點的數字是n.
課例解讀:著名數學家華羅庚曾說:“就數學本身來說,是壯麗多彩、千姿百態、引人入勝的……”入迷才能叩開思維的大門,智力和能力才能得到發展. 拓展后的引題,難度更大,此時,C層學生已無力招架,D層學生不由自主地沉迷變題,不能自拔. 解答中,同學們圍繞變題在組內、組間展開了激烈的討論,學生的數學素養在激情和體驗中得到升華,課堂上呈現了一場精彩絕倫的思維盛宴.
師:如果將“教學拓展”中的變題再加一個條件:如圖3,若只能沿線向下和向右運動,則從甲處到乙處的路線中經過丙處的有多少條?
有了剛才一問的鋪墊,同學們對此類變題已駕輕就熟,解法如泉水般涌來:
生10:第一段,觀察圖4,運用加法原理發現從甲處到丙處的路線有3條.
生11:第二段,觀察圖5,運用加法原理發現從丙處到乙處的路線也有3條.
目前,分層走班模式已在我校開展三年. 三年的課改實踐中,我們發現:分層走班模式讓數學課堂教學變得更自由、更靈活. “自主思考,重點展開,分步推進”策略在數學課堂教學中的運用讓學生的數學思維變得更活躍、邏輯變得更清晰. 學生喜歡這樣的課堂,家長認同這樣的課堂,教師愿意參與這樣的課堂. 筆者有理由相信:這樣的教育才是最適合學生的教育,是最好的教育!

