導數(shù)在高中數(shù)學函數(shù)中的應(yīng)用體會探索

黃書龍

【摘 要】導數(shù)屬于一個比較特殊的函數(shù)，同時，導數(shù)的引出以及相關(guān)的定義都涵蓋了函數(shù)的基本思想，新課程的改革中，也對導數(shù)的具體知識內(nèi)容進行了相應(yīng)的深化，同時切線、不等式以及數(shù)列等都帶來了新的解決思路，對眾多數(shù)學理論知識提供了更加便捷的解決方法。本文重點研究的是導數(shù)在高中數(shù)學函數(shù)教學中的具體應(yīng)用，分別從函數(shù)圖像的具體作法，函數(shù)具體單調(diào)性進行討論以及函數(shù)具體的最值求解方法等三個方面進行分析。

【關(guān)鍵詞】導數(shù)；高中數(shù)學；函數(shù)；應(yīng)用；體會與探究

隨著我國對高中課程的不斷改革，高中數(shù)學的相關(guān)教學也逐漸從理論知識教學轉(zhuǎn)化成實用性知識教學。導數(shù)的相關(guān)理論知識在研究曲線具體的切線以及解決實際問題中具有非常廣泛的應(yīng)用，于此同時，導數(shù)對于研究函數(shù)具體的單調(diào)區(qū)間，以及函數(shù)相應(yīng)的最值問題，證明不等式，對方程進行求解，數(shù)列的求和等各個數(shù)學方面的知識都提供了非常便捷的解決方法，因此，導數(shù)的學習在高中數(shù)學的學習中占有非常重要的位置。利用導數(shù)的相關(guān)理論知識能夠深入研究物理運動的具體變化，在如今現(xiàn)代化建設(shè)的眾多領(lǐng)域中都具有非常廣泛的應(yīng)用。導數(shù)對高中數(shù)學的學習也具有非常重要的引導作用。本文主要研究的是導數(shù)在高中數(shù)學函數(shù)學習中的具體應(yīng)用。

一、函數(shù)圖像的具體作法

在高中數(shù)學的教材中，利用描點的方法作出各種函數(shù)圖像，但是作圖的過程以及效果都比較粗糙，并且并不十分準確，一般情況下，這種描點的方式只適用于一些非常簡單的函數(shù)圖像，對于一些非常復雜的函數(shù)，利用描點的方式很難做出相應(yīng)的圖像。現(xiàn)在利用導數(shù)的相應(yīng)理論知識能夠非常容易地做出比較準確的函數(shù)圖像，同時方法比較方便簡單。利用導數(shù)的相關(guān)內(nèi)容分析整個函數(shù)具有的基本性質(zhì)，判斷函數(shù)呈現(xiàn)的單調(diào)性，最后求出函數(shù)的最值等內(nèi)容，得出比較準確的函數(shù)圖像。

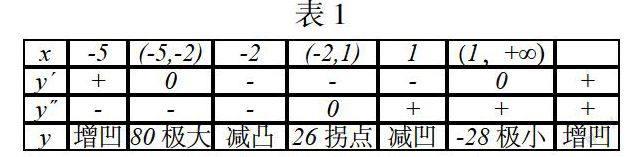
例1：做函數(shù)圖像y = x3+6x2?15x?20.

解：

得出函數(shù)具體的定義域為（?∞，+∞）。

（2）其中曲線與x以及y軸之前的交點為，（-1，0），（0，-20）。

（3）設(shè)y′=3x2+12x?15=0，最后解得數(shù)值x=?5或者x=1。

設(shè)y′′=6x+12=0，最后解得數(shù)值x=?2。

（4）通過列表的方式討論函數(shù)具有的單調(diào)區(qū)間，函數(shù)的極值點，函數(shù)的凸性區(qū)間以及函數(shù)的拐點，如表1。

（5）不存在漸進線。

（6）根據(jù)具體數(shù)值做出最終的圖像。

二、函數(shù)具體單調(diào)性進行討論

函數(shù)具有單調(diào)性是所有函數(shù)自身具有的最基本的性質(zhì)，也是對函數(shù)進行研究需要了解的基本的數(shù)學理論知識。單調(diào)性具體的定義對于處理各種單調(diào)性相關(guān)的問題具有非常強的技巧性，并且掌握起來并不容易，利用導數(shù)的相關(guān)知識內(nèi)容判斷函數(shù)具有的單調(diào)性，非常簡短便捷，并且容易掌握，理解起來比較容易。

例2：函數(shù)f（x）=x3-3x，確定這一函數(shù)具體在哪一個區(qū)間呈現(xiàn)的是增函數(shù)，在哪一個區(qū)間呈現(xiàn)的是減函數(shù)。

分析：對上述函數(shù)進行求導，并且，求不等式f′（ x）<0以及f′（x）>0具體的解，其中，f′（x）<0具體的解就是整個函數(shù)的單調(diào)區(qū)間。

解：由于函數(shù)具體的導數(shù)函數(shù)為f′（x）=3（x+1）（x-1），設(shè)f（x）′>0，最終可以得出x<1或者是x>1，因此上述函數(shù)具體的單調(diào)增區(qū)間是（?∞，?1）以及（1，+∞）。

函數(shù)具體的最值的求解方法

函數(shù)最值的相關(guān)問題也屬于高中數(shù)學學習中的一個非常重要的知識內(nèi)容，也屬于高中數(shù)學的重點難點，函數(shù)的最值問題涉及到高中數(shù)學中各個方面的理論知識，涉及的面非常廣泛，利用導數(shù)解決函數(shù)的最值問題，能夠有效地簡化整個解題的過程，并且整個過程也非常廣泛，步驟比較清晰明確，方便學生理解，并能更加清楚地掌握相應(yīng)的知識內(nèi)容。

一般情況下，函數(shù)的閉區(qū)間在[a，b]屬于可導區(qū)間，那么，函數(shù)在[a，b]這一區(qū)間具體的最值求法為，首先，需要求出函數(shù)在（a，b）上具體的駐點，其次，計算出函數(shù)在駐點以及端點內(nèi)具體的函數(shù)值，通過比較可以得出，其中最大的一個數(shù)值及時最大值，其中最下的一個數(shù)值就是最小值。實際上，這一解決的方案可以利用本文中的第一個性質(zhì)進行解答，也就是利用作圖的方式解答。因此，在進行作圖的整個過程中，需要求出具體的極值點以及函數(shù)的最值點，因此，利用作圖的方式或者是利用求最值的方法都存在一些非常相似的步驟以及相同的數(shù)學思維方法。

例3：函數(shù)f（x）=x3-x2/2-2x+c2，如果，x∈[?1，2]，那么f（x）

分析：面對這樣的數(shù)學題目，想要找出解題的方法最重要就是要深刻地理解函數(shù)的相關(guān)理論知識，并學會靈活的運用，上題中，問題的實質(zhì)就是確定函數(shù)y=g（x）具體的最大值是多少。

解：設(shè)g（x）=x3-x2/2-2x，因此任意的x都有x∈[?1，2]，并且g（x）?c2-c恒成立，其中g(shù)′（x）=（x?1）（3x+2），如果x發(fā)生一定的變那么g（x）以及g′（x）也會同時發(fā)生變化，由于g（2）=2，因此，對于任意的x，并且x∈[?1，2]，函數(shù)最大值為g（2）=2。最終得出，c∈（?∞，?1）∪（2，+∞）。

三、結(jié)束語

綜上所述，導數(shù)是解決數(shù)學眾多問題的一個關(guān)鍵工具，利用導數(shù)的數(shù)學思想對解決眾多數(shù)學問題都具有非常重要的意義，也提供了一些非常方便簡單的解題方法。尤其是利用導數(shù)的相關(guān)知識內(nèi)容解決函數(shù)具有單調(diào)性、極值以及最值等數(shù)學問題中，非常方便并且容易掌握。在利用導數(shù)解決各種數(shù)學問題的整個過程中，能夠引入非常優(yōu)化的數(shù)學思維方法，整個解題過程也非常簡單便捷，掌握了數(shù)學導數(shù)的相關(guān)知識內(nèi)容，為高中學生提供了一種更加方便的數(shù)學解題工具，幫助學生深入地理解函數(shù)的基本概念，并通過導數(shù)直觀地認識與理解函數(shù)的相關(guān)理論知識內(nèi)容。

參考文獻：

[1]丁偉.中學數(shù)學教學參考[J].陜西師范大學中學教學參考雜志社出版，2010

[2]畢明黎，王麗.中學數(shù)學研究[J].華南師范大學數(shù)學科學學院，2011，（3）

[3]高慧明.中學數(shù)學研究[J].華南師范大學數(shù)學科學學院，2011，（9）