學(xué)會(huì)質(zhì)疑，學(xué)會(huì)學(xué)習(xí)

陳英

【摘要】 作為學(xué)生思維習(xí)慣的形成階段，初中時(shí)期是教師們需要特別注意的時(shí)期，尤其是數(shù)學(xué)學(xué)科，它是所有理科的基礎(chǔ)學(xué)科，在數(shù)學(xué)學(xué)習(xí)中，如果能夠讓學(xué)生養(yǎng)成良好的質(zhì)疑習(xí)慣，培養(yǎng)出學(xué)生高質(zhì)量的質(zhì)疑能力，那么，在接下來(lái)各科的學(xué)習(xí)中，學(xué)生都能受益匪淺.所以，教師在教學(xué)過(guò)程中，要想辦法把課堂的質(zhì)疑氛圍與主動(dòng)思考氛圍營(yíng)造起來(lái)，以激發(fā)學(xué)生對(duì)現(xiàn)有知識(shí)提出質(zhì)疑.

【關(guān)鍵詞】 初中數(shù)學(xué)；引發(fā)疑問(wèn)；質(zhì)疑能力

愛(ài)因斯坦說(shuō)：“提出一個(gè)問(wèn)題，往往比解決一個(gè)問(wèn)題更重要.”這個(gè)說(shuō)法在數(shù)學(xué)學(xué)習(xí)中特別適用.數(shù)學(xué)本來(lái)便是一個(gè)探索性的學(xué)科，學(xué)生通過(guò)對(duì)問(wèn)題的鉆研，利用教師教給他們的理論知識(shí)來(lái)進(jìn)行問(wèn)題的解決，從中找到多種解題思路，并從中發(fā)現(xiàn)新的問(wèn)題.而對(duì)于一個(gè)問(wèn)題，學(xué)生能夠迅速地從中提出各種疑問(wèn)，這就是學(xué)生的質(zhì)疑能力.初中是學(xué)生思維模式與思維習(xí)慣定式的階段，培養(yǎng)學(xué)生的質(zhì)疑能力便尤為重要. 當(dāng)前的教學(xué)多數(shù)是以考試為主，以學(xué)生掌握解題方法為最終目的，而這中間，學(xué)生如果遇到難題無(wú)法解決，才向教師提出問(wèn)題，而面對(duì)既定的解決思路，卻沒(méi)有質(zhì)疑的習(xí)慣.作為教師的我們，應(yīng)該從學(xué)生的長(zhǎng)遠(yuǎn)發(fā)展考慮，利用課堂以及習(xí)題來(lái)培養(yǎng)學(xué)生的質(zhì)疑能力，為他們此后更深層次的發(fā)展打下基礎(chǔ).

一、通過(guò)比較，引發(fā)疑問(wèn)

“溫故而知新”是我國(guó)教育千百年來(lái)的至理名言，數(shù)學(xué)的新知識(shí)與舊知識(shí)之間往往存在著諸多關(guān)聯(lián)，當(dāng)然，這些關(guān)聯(lián)的知識(shí)之間肯定是有著諸多不同的.如果在教學(xué)過(guò)程中，教師不提舊知識(shí)，也可能會(huì)有一部分學(xué)生能聯(lián)想到學(xué)過(guò)的知識(shí)，但是，即使聯(lián)想到了，也不一定就會(huì)主動(dòng)將它們之間的區(qū)別與聯(lián)系總結(jié)起來(lái)，無(wú)法形成一個(gè)系統(tǒng)的知識(shí)鏈，而更多的學(xué)生壓根就不會(huì)去想那么多，他們更習(xí)慣接受教師的傳授與引導(dǎo)，教師指到哪兒，他們就學(xué)到哪兒.所以，教師在教學(xué)的過(guò)程中，便可以利用前后知識(shí)的比較，引發(fā)學(xué)生們的疑問(wèn)，從而激發(fā)學(xué)生們的探究欲望，讓他們主動(dòng)去解決問(wèn)題，并在這個(gè)過(guò)程中鞏固了學(xué)過(guò)的知識(shí)，學(xué)到了新的知識(shí)，同時(shí)將它們系統(tǒng)地串聯(lián)在一起，形成一個(gè)知識(shí)鏈.

比如學(xué)習(xí)“相似圖形”這節(jié)課，我便利用之前學(xué)過(guò)的“全等圖形”作為引子來(lái)引出這節(jié)課的內(nèi)容. 我首先畫(huà)了兩組圖形，每組有四個(gè)，第一組是長(zhǎng)方形，兩個(gè)是全等的，一個(gè)是等比例縮小的，還有一個(gè)與它們完全不同；第二組是四角形，兩個(gè)是全等的，一個(gè)是等比例放大的，另外一個(gè)是隨便畫(huà)的三角形.首先，因?yàn)閷W(xué)過(guò)全等圖形，所以，在我畫(huà)出兩個(gè)全等的三角形和兩個(gè)全等的長(zhǎng)方形的時(shí)候，大家都能迅速地說(shuō)出它們的特點(diǎn).然后，我又畫(huà)出等比例縮小的長(zhǎng)方形以及等比例放大的三角形.我將長(zhǎng)方形的長(zhǎng)寬比列出來(lái)，大家發(fā)現(xiàn)比例是一樣的.然后大家又發(fā)現(xiàn)大小、三角形的三個(gè)角度數(shù)是一樣的.顯然，這兩組圖形中，縮小和放大版的，與另外兩個(gè)全等版的，是有著一定的關(guān)聯(lián)的，而隨便畫(huà)的與它們毫無(wú)關(guān)聯(lián)的長(zhǎng)方形或三角形，又是各自一體，我讓大家對(duì)比它們之間的數(shù)據(jù)，發(fā)現(xiàn)了這其中的奧妙，同學(xué)們就會(huì)想，是不是這個(gè)等比例的，跟這兩個(gè)全等的有什么其他的關(guān)系呢？因?yàn)樗煌谌鹊膱D形，同時(shí)又跟它們之間存在著一定的規(guī)律，所以，它們應(yīng)該存在著某種關(guān)系，是不是有什么公式來(lái)表現(xiàn)這種特殊的關(guān)系？這樣，通過(guò)幾種對(duì)比，引出了學(xué)生們的疑問(wèn)，讓他們從這些圖形之間的關(guān)系中，找到了它們潛在的規(guī)律，并引出了我們要學(xué)習(xí)的內(nèi)容：相似圖形.

數(shù)學(xué)的很多知識(shí)點(diǎn)都是彼此相通的，有著一定的聯(lián)系，同時(shí)存在著差異，所以，通過(guò)對(duì)比的方法來(lái)引出知識(shí)點(diǎn)，不僅能讓學(xué)生們復(fù)習(xí)已經(jīng)學(xué)過(guò)的知識(shí)，還能讓學(xué)生們從中找到新的知識(shí)源泉. 葉圣陶說(shuō)，教學(xué)的意義不是全盤(pán)托出按部就班，而是適時(shí)地進(jìn)行引導(dǎo)，讓學(xué)生自己找到知識(shí)的存在.新舊知識(shí)的對(duì)比能讓學(xué)生們找到它們的規(guī)律，從而發(fā)現(xiàn)新知識(shí).

二、產(chǎn)生矛盾，激起思考

著名的心理學(xué)家皮亞杰曾說(shuō)過(guò)：“一切真理要由學(xué)生自己獲得，或由他們重新發(fā)現(xiàn)，至少由他們重建.”讓學(xué)生去重新發(fā)現(xiàn)問(wèn)題，作為教師的我們就要巧設(shè)矛盾讓學(xué)生們?nèi)ニ伎歼@個(gè)矛盾的成因，以及如何來(lái)解決這個(gè)矛盾，那么，這個(gè)矛盾背后所代表的真理，便等于是由學(xué)生們重新發(fā)現(xiàn)，這樣，不僅能令學(xué)生從根本上自主地去理解問(wèn)題，更能推進(jìn)教學(xué)的高效性，以及學(xué)生主動(dòng)探索的精神.而這種矛盾的產(chǎn)生，往往是相近、相似的題型，或者是針對(duì)一些知識(shí)點(diǎn)的特性，從其中一點(diǎn)入手，利用學(xué)生考慮不夠全面的特點(diǎn)來(lái)產(chǎn)生，讓學(xué)生對(duì)此產(chǎn)生質(zhì)疑，從而對(duì)其進(jìn)行深入的思考，最終解決這個(gè)問(wèn)題.

例如在“平行四邊形、矩形、菱形、正方形的性質(zhì)和判定”這節(jié)課中，在講完平行四邊形以及矩形和菱形的性質(zhì)和判定之后，我又給大家畫(huà)出了幾個(gè)圖形，平行四邊形、矩形、菱形、正方形，并把這幾個(gè)圖形相對(duì)應(yīng)的數(shù)據(jù)條件都列了出來(lái)，四條邊的長(zhǎng)度以及四個(gè)角的角度等.然后我問(wèn)大家，我畫(huà)的最后一個(gè)圖形，也就是正方形，它應(yīng)該屬于矩形還是屬于菱形，還是屬于平行四邊形？這個(gè)問(wèn)題提出后，大家的意見(jiàn)便各不相同了，矛盾也由此而生，有人認(rèn)為它屬于矩形，有人認(rèn)為它屬于菱形，當(dāng)然，也有同學(xué)說(shuō)它應(yīng)該是屬于又一種特殊的平行四邊形，但是，很顯然，大家都說(shuō)得有理有據(jù)，而且大家所說(shuō)的道理都是立得住腳的，也就是說(shuō)，大家所得到的結(jié)論都是成立的，因?yàn)榇蠹叶寄芡ㄟ^(guò)論證來(lái)證明自己的觀點(diǎn)，矛盾就集中在：它到底是屬于哪一種呢？菱形，它是；矩形，它是；平行四邊形，不用說(shuō)，肯定是了.于是，大家在對(duì)這個(gè)矛盾的解決過(guò)程中，無(wú)疑便是將這個(gè)圖形（正方形）的性質(zhì)一點(diǎn)一點(diǎn)地挖掘、研究了出來(lái)，而最后，教師要做的，就是將大家所研究出來(lái)的這個(gè)圖形（正方形）的性質(zhì)來(lái)做一個(gè)總結(jié).

可以說(shuō)，在很多的數(shù)學(xué)知識(shí)中，如果不曾學(xué)過(guò)更深的知識(shí)，它們的矛盾是普遍存在的，教師將這種矛盾良好地呈現(xiàn)出來(lái)，讓學(xué)生們對(duì)學(xué)問(wèn)產(chǎn)生質(zhì)疑，從而讓他們學(xué)會(huì)思考這其中的奧妙，并最終找到正確的答案，不僅能夠讓學(xué)生自己發(fā)現(xiàn)真理，更是讓教師也輕松提升了課堂效率.

三、總結(jié)解法，提出想法

俗話說(shuō)，條條大路通羅馬，有時(shí)候，一道題有多種解法，而這些解法最終都能得到一個(gè)正確的答案，只是它們所利用的原理不同，各種解法殊途同歸，最終都能完成題目的解答.而這個(gè)時(shí)候，就是讓學(xué)生們自己去思考這些解法之間的異同以及哪個(gè)更便捷的時(shí)候，教師在這種情況下不要限定于其一種便捷的方法來(lái)給學(xué)生們講，要讓學(xué)生們?cè)诳偨Y(jié)了各種解法之后，自己去提出自己的想法，讓他們自己去感受，哪個(gè)解法才是最簡(jiǎn)單的，甚至是讓學(xué)生們提出更多的想法，看能否解答出題目來(lái).

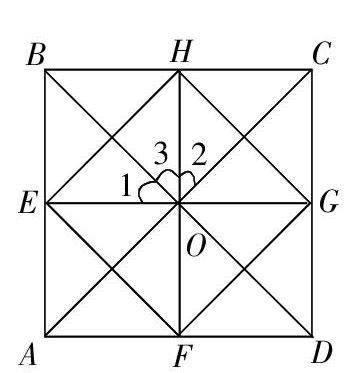
例如這個(gè)習(xí)題：如圖所示，已知四邊形ABCD為正方形，O為對(duì)角線交點(diǎn)，E，F(xiàn)，H，G分別是四條邊的中點(diǎn).求證：四邊形EFGH是正方形.

這是一道非常簡(jiǎn)單的證明題，屬于初步練習(xí)題的范圍.在證明四邊形EFGH是正方形的過(guò)程中，可以有多種方法，首先，可以論證它們的對(duì)角線HF，EG互相垂直平分且相等，從而證明四邊形EFGH是正方形；其次，可以先證明其為平行四邊形，再證明有一個(gè)角是直角，同時(shí)有兩條鄰邊相等，從而證明四邊形EFGH是正方形；再者，還可以論證有三個(gè)內(nèi)角都是直角，并且有一組鄰邊相等……可以說(shuō)，這道簡(jiǎn)單的習(xí)題，能夠?qū)⒄叫蔚乃信卸ǘɡ矶加靡槐椋叶寄軌虻玫阶C明的結(jié)果.我將這些解法給大家總結(jié)了之后，有名同學(xué)又提出了另外一個(gè)想法，他告訴我說(shuō)，如果反過(guò)來(lái)，這道題沒(méi)有指明E，F(xiàn)，G，H是四條邊的中點(diǎn)，但是，只要知道四邊形EFGH某一個(gè)角是直角，便可以證明它是正方形.他的想法馬上得到了同學(xué)們的響應(yīng)，大家又提出了其他的想法. 最后，簡(jiǎn)簡(jiǎn)單單的一道小證明題，最終卻得到了意想不到的收獲.學(xué)生們?cè)诖税l(fā)散了思維，找到了更多的方法，甚至是對(duì)這道題進(jìn)行了延伸.

所以，這種看似簡(jiǎn)單的不值一講的習(xí)題，教師也不要簡(jiǎn)單地通過(guò)一種方式將之概括過(guò)去，誠(chéng)然，這種習(xí)題對(duì)多數(shù)學(xué)生來(lái)說(shuō)，甚至是不用思考便能解答的，但是，教師詳細(xì)的講解并不只是為了這一道題，而是要讓學(xué)生在教師的總結(jié)中，發(fā)現(xiàn)它的新的延伸，對(duì)它產(chǎn)生新的想法.不要怕浪費(fèi)時(shí)間總結(jié)解法，它最終能夠引起學(xué)生們向更深入的方向去思考，從而提出新的想法.

有質(zhì)疑，繼而才會(huì)有知識(shí)的進(jìn)一步延伸，科學(xué)的進(jìn)一步發(fā)展，作為所有理科的基礎(chǔ)學(xué)科，在初中數(shù)學(xué)教學(xué)的過(guò)程中，采用相應(yīng)的措施來(lái)培養(yǎng)學(xué)生的質(zhì)疑能力，不僅是為當(dāng)前學(xué)生的學(xué)習(xí)打開(kāi)思路，更是為其接下來(lái)更深層次的學(xué)習(xí)與研究做好鋪墊.