精準(zhǔn)構(gòu)建幾何思維 創(chuàng)設(shè)高效數(shù)學(xué)課堂

陳曉靜

摘要：數(shù)學(xué)思維的訓(xùn)練對于學(xué)生學(xué)好數(shù)學(xué)這門學(xué)科至關(guān)重要，特別是發(fā)散性思維能夠開拓學(xué)生的思路、培養(yǎng)學(xué)生靈活的學(xué)習(xí)思維，讓學(xué)生在解題過程中不局限于一個(gè)解題方法。本文主要從一題多解、一題多問、一題多變等方面來闡述怎樣培養(yǎng)學(xué)生的發(fā)散思維。

關(guān)鍵詞：初中數(shù)學(xué) 幾何數(shù)學(xué)? 發(fā)散思維

發(fā)散思維就是從已知條件、規(guī)律、方法、概念出發(fā)，對問題的解決不按常規(guī)，而產(chǎn)生另一種或多種想法的思維方式。發(fā)散性思維可激發(fā)發(fā)學(xué)生的學(xué)習(xí)動機(jī)、啟迪思想、激發(fā)求知欲、探索欲和創(chuàng)新欲等。因此，在初中數(shù)學(xué)幾何教學(xué)中，鼓勵(lì)他們勇于創(chuàng)新、發(fā)散思維，使得學(xué)生從多方面、多層次以及多角度進(jìn)行思考，探索出獨(dú)特、新穎、簡單的解題方法是非常重要的。

一、一題多解，激發(fā)學(xué)生的求知欲

思維循規(guī)蹈矩是學(xué)生發(fā)散思維培養(yǎng)的主要障礙，如果學(xué)生的思維積極性較強(qiáng)，則有利于發(fā)散思維的培養(yǎng)。通過一題多解的方法讓學(xué)生從不同角度思考問題、解決問題，可以引起學(xué)生強(qiáng)烈的求異欲望，培養(yǎng)學(xué)生思維的靈活性以及求同存異的思維能力。

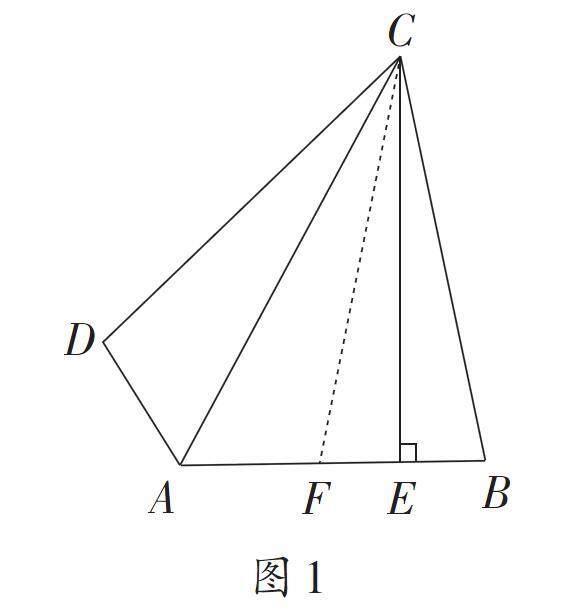
案例1? 已知，AC平分∠BAD，CE⊥AB，∠B+∠D=180°，求證：AE=AD+BE。

點(diǎn)撥? 一般來說，“證明兩條線段的和等于第三條線段”時(shí)，常用的方法是截長補(bǔ)短法。截長法是指在第三條線段即最長的線段上截取一段等于較短兩條線段中的一條，然后再證最長線段上所剩的部分，等于兩條短線段中的另一條。補(bǔ)短法是指把兩條較短線段接起來，然后證所得的最長線段等于第三條線段；根據(jù)這種思路我們就有兩種證明方法。

證明一? 如圖1，在AE上取點(diǎn)F，使EF=BE，

由CE⊥AB有，△CEF≌△CEB，

∴ ∠CFE=∠B

∵ ∠B+∠D=180°

∴ ∠CFA=180°－∠CFE=∠D

∵ AC平分∠BAD

∴ △ADC≌△AFC

∴ AD=AF

∴ AE=AF+FE=AD+BE

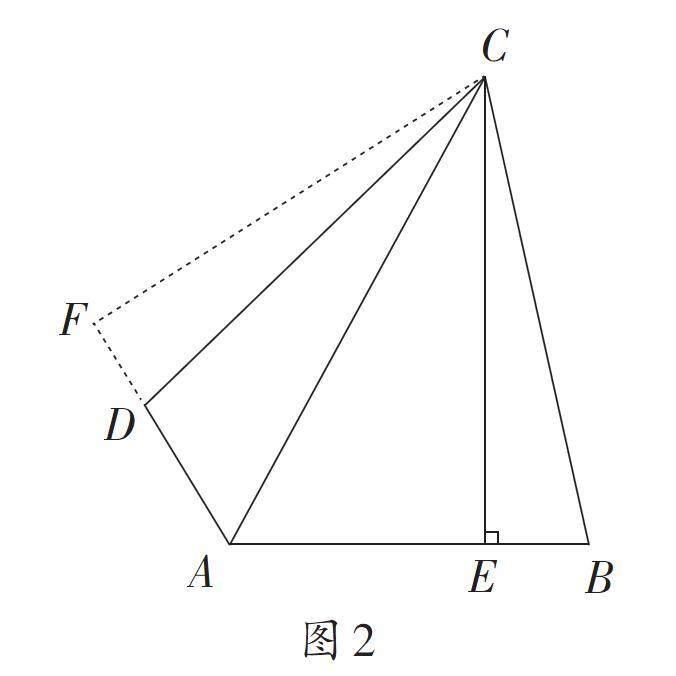
證明二? ?如圖2，延長AD到點(diǎn)F，使AF=AE，

由AC平分∠BAD，易證 △AFC≌△AEC

∴ ∠F=∠AEC，CF=CE

又∵ CE⊥AB

∴ ∠CEB=∠AEC=90°

∴ ∠F=∠CEB

∵ ∠B+∠ADC=180°，∠FDC+∠ADC=180°

∴ ∠CDF=∠B

∴ △DCF≌△BCE

∴FD=BE

∴ AF=FD+AD=BE+AD

即AE=AD+BE

通過一題多解，可以加深學(xué)生對題目的形式、組成元素以及題目隱含的邏輯（因果）關(guān)系的認(rèn)識，從而培養(yǎng)了學(xué)生數(shù)學(xué)洞察力和推理能力，更重要的是培養(yǎng)了學(xué)生的發(fā)散思維，有利于學(xué)生今后在解決數(shù)學(xué)問題時(shí)拓寬解題思路，提高解題的靈活性。

二、一題多問，培養(yǎng)學(xué)生的發(fā)散性思維

要培養(yǎng)學(xué)生的發(fā)散性思維，首先要改變學(xué)生固有的思維模式，從多角度進(jìn)行思考，這也是學(xué)生思維的求異性。要訓(xùn)練以及培養(yǎng)學(xué)生抽象思維能力，就要注重培養(yǎng)思維的求異性，讓學(xué)生從多個(gè)角度來分析問題，最終探索出一條簡便、新穎的解題思路。

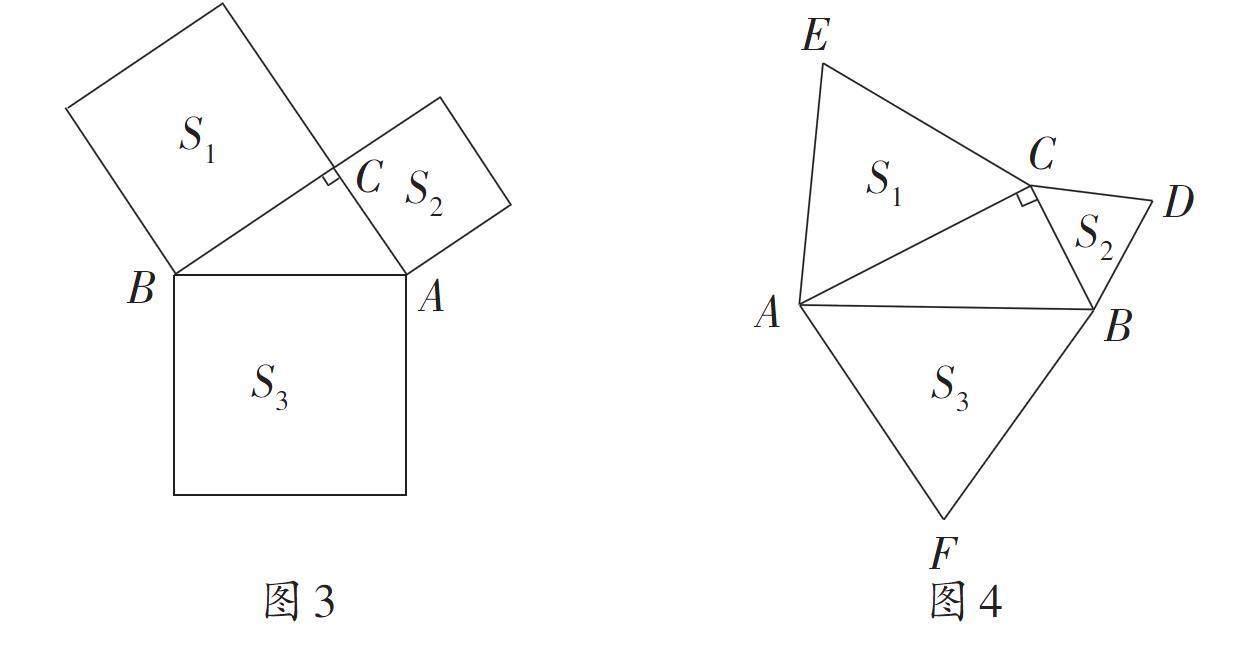
案例2 上完八年級上冊“2.7探索勾股定理”內(nèi)容后，我安排了從勾股定理到圖形面積關(guān)系的拓展，我們知道，勾股定理反映了直角三角形三條邊之間的關(guān)系：a2+b2=c2。而a2，b2，c2又可以看成是以a，b，c為邊長的正方形的面積，因此，勾股定理也可以表述為：分別以直角三角形兩條直角邊為邊長的兩個(gè)正方形的面積之和，等于以斜邊為邊長的正方形的面積，如圖3，即S1+S2=S3。

如果以直角三角形的三條邊a，b，c為邊，向外分別作正三角形，那么是否存在S1+S2=S3呢？如圖4，引導(dǎo)學(xué)生根據(jù)正三角形的面積公式，得到

S3=[34c2]，S1=[34a2]，S2=[34b2]

∵ △ABC是直角三角形，

∴ a2+b2=c2

經(jīng)過分析，發(fā)現(xiàn)以直角三角形的三條邊a，b，c為邊向外分別作正三角形，同樣能得到S1+S2=S3。

類似地，上述結(jié)果是否適合其他圖形呢？分別以直角三角形的三條邊a，b，c為邊向外分別作半圓，作等腰直角三角形，則S1+S2=S3依然成立嗎？再畫幾個(gè)類似的圖試一試。

通過上述這么多問題的探討，學(xué)生的思維得到了更好的拓展，分別以直角三角形ABC三邊為一邊向外作相似圖形，其面積分別用S1、S2、S3表示，則S1+S2=S3都成立 。

三、一題多變，培養(yǎng)學(xué)生的思維廣闊性

思維廣闊性是發(fā)散思維的一大特征，在初中幾何數(shù)學(xué)教學(xué)過程中，通常有一些學(xué)生對于知識一知半解，在解決問題時(shí)往往存在一定的片面性，要改變這種狹隘性思維，老師在課堂上應(yīng)該對同一類型的題目進(jìn)行引申和多解，讓學(xué)生分組討論，如此不但拓寬了學(xué)生解題思路，也使得他們的發(fā)散思維得到培養(yǎng)。

案例3? 已知，如圖5，在△ABC中，點(diǎn)D，E分別在AB，AC邊上，F(xiàn)是CD中點(diǎn)，連BF交AC于點(diǎn)E，∠ABE+∠CEB=180°，判斷BD與CE的數(shù)量關(guān)系，并證明你的結(jié)論。

結(jié)論：BD=CE

證明? 延長BF至點(diǎn)G，使FG=BF，連CG，

∵ F為CD中點(diǎn)，? ∴ CF=DF

在△GFC和△BFD中，

FG=BF，∠GFC=∠DFB，CF=DF

∴ △GFC≌△BFD（SAS）

∴ ∠CGF=∠FBD，CG=DB

又∵ ∠ABE+∠CEB=180°，∠CEG+∠CEB=180°，

∴ ∠CGF=∠CEG

∴ CG=CE? ? ∴ BD=CE

變式? 已知，如圖6，點(diǎn)D在等邊三角形ABC的邊AB上，點(diǎn)F在邊AC上，連接DF并延長交BC的延長線于點(diǎn)E，EF=FD。求證：AD=CE。

證明? 作DG∥BC交AC于G，如圖所示，則

∠DGF=∠ECF，

在△DFG和△EFC中，

∠DGF=∠ECF，∠DFG=∠EFC，F(xiàn)D=EF，

∴ △DFG≌△EFC（AAS），

∴ GD=CE，

∵ △ABC是等邊三角形，

∴ ∠A=∠B=∠ACB=60°，

∵ DG∥BC，

∴ ∠ADG=∠B，∠AGD=∠ACB，

∴ ∠A=∠ADG=∠AGD，

∴ △ADG是等邊三角形，

∴ AD=GD

∴ AD=CE

這兩個(gè)題目從本質(zhì)上看，是比較相似的，然而單獨(dú)拿出來給學(xué)生做的時(shí)候，學(xué)生卻不知道該如何下手，所以在教學(xué)中將這個(gè)題目安排在一起，通過變式的形式讓學(xué)生尋找它們的本質(zhì)，從而讓學(xué)生的數(shù)學(xué)思維得到更好的發(fā)展。