GGb軟件與高三數學教學的深度融合

劉健康

【摘要】GeoGebra（簡稱GGb），作為功能強大的數學制圖工具，具有動態、可視化的特點，能夠很好地將高中數學中比較抽象、空間思維強的知識點以一種真實的情景再現。動態的過程演變，可變化的形式展現，可以激發學生的學習興趣，快速理解數學的本質。目前，GGb在我國得到廣泛的運用和推廣。本文根據高三數學教學的積累，從幾個實例闡述GGb在高三數學教學上的應用，提高教學效率。

【關鍵詞】GGb;高三數學;數學教學

信息技術與學科教學的融合，是改變傳統教學模式的重要舉措。目前的教學中，部分老師對教育信息化發展的重要性存在認識不足，個別老師還堅持“粉筆+教材”的傳統模式，有的老師只會點擊教輔的PPT，不做改動和選擇，有的條件好的學校提供希沃白板設備，老師也就只是用來代替粉筆書寫。這些缺乏主動意識的行為，導致課堂質量、效率及效果較低。隨著國家“雙減”政策的實施，提高課堂教學效率、效果勢在必行。

GGb是一個動態幾何軟件。教師可以通過操作GGB 的滑動條、動點、制作動畫讓學生感受數學動態的過程，在掌握數學知識的過程中體會數形結合的樂趣。利用GGB 使學生經歷數學知識的發生以及問題的發現、提出、分析以及解決的過程。利用3D 繪圖區，增加立體幾何教學的直觀性，降低抽象難度，減少學生學習過程中的障礙，增加學生的學習興趣，激發抽象思維的同時減少學生學習的畏難情緒。

一、GGb軟件在高三數學概念教學中的應用

在高三教學中，概念復習教學特別重要，教師應該從多角度充分揭示概念的內涵和外延，引導學生對概念進行本質的理解和提升。眾所周知，三角函數線這個概念是個教學難點，學生普遍感覺困難，新教材也意識到這一點。其實三角函數線就是三角函數的幾何特征，體現了數學中代數與幾何的交匯，有數形結合的思想運用。有了GGb，我們可以結合動態展現，根據學生已學向量知識，更清晰掌握這個概念。

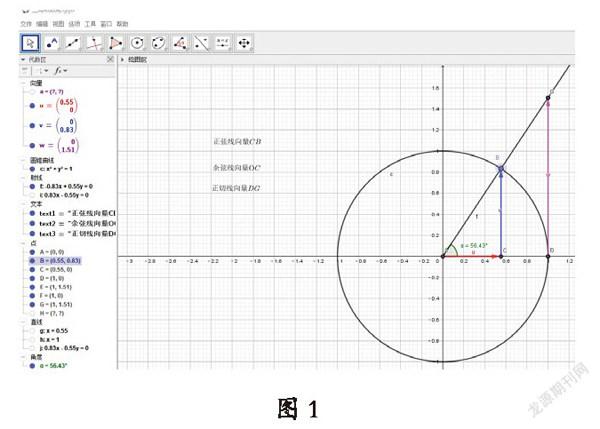
第一，設計意圖：角α的正弦值，余弦值，正切值都是“數”，而對應正弦線、余弦線、正切線都是“形”。通過 GGb 的動態呈現，步步有據，形象直觀，可以得到結論：任意角α的三角函數線就是對應的向量，這些向量的數值就是對應的角α的三角函數值。

第二，技術操作。如圖1所示：（1）用畫圓工具做出單位圓;（2）用描點工具在單位圓上任取點B;（3）用直線工具做出射線OD，向量CB，OC，DG;（4）點擊B點屬性，開啟動畫。

圖1

第三，操作點評。制圖時要注意角α旋轉到第二、三象限時，正切線是反向延長的相交。讓學生密切注意動點所在的位置。對每一個象限的特征加以區別，讓學生通過觀察后，主動描述三角函數線的概念。

通過以上的教學過程，將數學概念動態化、直觀化，有效幫助學生理解概念本質，有利于培養學生的直覺思維能力和主動探究意識。通過促進學生形象思維的培養，進一步發展邏輯思維。

二、GGb 軟件在高三數學立體幾何教學中的應用

在高三教學中，立體幾何一直是高考的重點。需要培養學生的空間想象能力，掌握空間里點、線、面的原理，表達和位置關系，熟悉柱體、錐體、臺體和更多組合幾何體的結構，還需要從坐標代數的角度進行各種距離、角度的計算，同時探索動態情況下的最值變化。學生空間思維能力不足，平面與空間的轉換方面有困難，學生如果不能夠正確理解立體幾何各定理，不能梳理好他們之間的關系，會導致學生思維受局限，不能正確全面認識立體圖形，就無法做出正確的證明和計算。以例1的教學為例。

例1：已知P，A，B，C，D是球O上的五個點，在四邊形ABCD中，AD//BC，AB=DC=AD=2，DC=PA=4，PA⊥面ABCD。求球O的體積。

學情分析：底面是等腰梯形，需要底面外接圓，部分學生無法正確作出，不能判斷圓心位置，大部分學生沒有尋找球心位置的正確方向，不會用球心和圓心的連線垂直外接圓面的關系。

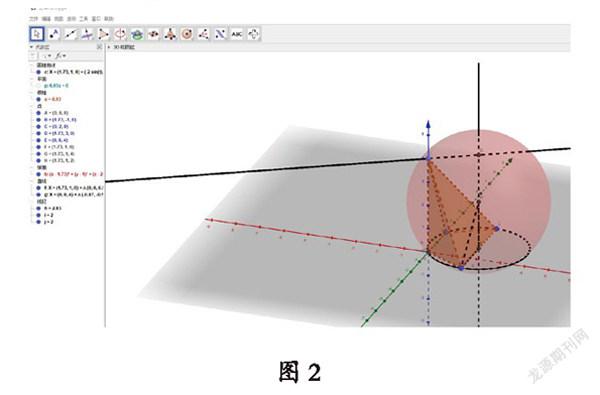
解決辦法：用GGb畫出底面外接圓，讓學生體會外接圓圓心的位置，引導學生證明圓心是BC的中點，再用GGb找出球心位置，讓學生充分認識立體結構、線面關系，找到計算球半徑的三角形。

技術操作：如圖2所示：（1）在3D繪圖區用描點工具找到五個點，用錐體工具連成棱錐;（2）用作圓工具點擊A，B，C三點做出外接圓，確定圓心;（3）用垂線工具點擊圓心，外接圓面，作出垂線，再過P點做剛才垂線的垂線;（4）用中點工具確定球心，用多邊形工具連接球心，圓心，球面上點，連成三角形;（5）三角形中的計算球半徑。

操作點評：在用GGb 展示知識重難點的同時，還要注意課件中的顏色搭配以及信息布局，讓學生可以一眼就抓住課件中所要呈現的重要信息，形成記憶點。其次，還可以通過GGb的復原、重復、隱藏、顯示、拖動和動畫，配合生動有趣的語言對學生進行教學、反饋和探索。教學中，應把學生的直觀感受擺在重要位置，充分調動學生的感覺器官，讓學生能夠將自己的直觀感受作為出發點，概括出現象的本質及其規律。

三、GGb 軟件在高三數學綜合能力教學中的應用

新課標提出數學六大核心素養：數學抽象、邏輯推理、數學建模、直觀想象、數學運算、數據分析。其中，培養學生空間想象能力，發展形象思維、抽象思維是中學數學教學的重要內容。《高中數學新課程標準》《全日制義務教育數學課程標準》中提到注重信息技術和數學課程的有機整合，課堂上要盡可能使用多媒體設備、教學工具等，將抽象的數學問題直觀展現，營造輕松愉悅的多媒體教學環境，引導學生發現問題、提出問題、分析問題、解決問題，提高空間想象能力。以例2的教學為例。

例2：已知M為函數y=8/x?的圖像上任意一點，過M作直線MA，MB分別與圓x+y=1相切于A，B兩點，則原點O到直線AB的距離最大值為（? ? ）。

A.1/8?B.1/4? ?C. 根號2/2? D.根號2/24

學情分析：學生會習慣設M（x，y），做出圓的兩條切線后，不能準確求出直線AB的方程，從而用點到直線的距離公式解決不了問題。或者會沒有根據去猜測動點M的位置。

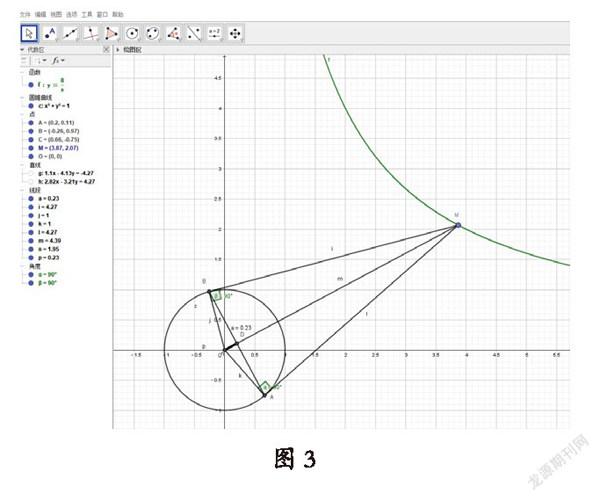
解決辦法：用GGb做出動態圖，在變化過程中顯示原點O到直線AB的距離的變化狀態和規律，體會M點的特殊位置，激發探索的興趣。教師再從代數和幾何兩方面培養學生的綜合能力，第一，用代數變換學習切點弦的求法，再用點到直線的距離公式，最后結合基本不等式知識。第二，從幾何角度，發現直角三角形中的射影定理，得到點到直線的距離和OM長度的關系，利用M點在曲線上，基本不等式求出最值。

技術操作：如圖3所示：（1）用畫圖工具做出單位圓;（2）直接輸入函數y=8/x，可以立即顯示曲線圖像;（3）用描點工具在y=8/x圖像上任取點M;（4）用作切線工具，點擊點M和圓O可作兩條切線;（5）用直線工具做出各條線段，標明垂直90度;（6）點擊點M的屬性，開啟動畫（也可以用滑動桿控制或者復選框）。

操作點評：GGb軟件的視圖工具、操作過程的功能，能夠體現數學思維過程，活躍課堂氛圍、提高學生參與度，但是課堂教學最后還是以學生為主體，信息技術是輔助手段，融合得很好，恰當的設計會效果顯著。演示的同時，教師要注意及時引導和歸納，最后形成知識點的傳授，培養學生的數學綜合能力。

四、GGb 軟件在高三數學教學中的應用意義和展望

多元表征理論提出：信息、資源（如數學概念或數學問題）通過建構心像碼，擔任“橋梁”角色，對信息進行編碼和形成多種轉譯方式，從而呈現對信息的多元化的表征。高三數學教學是多個模塊知識點的綜合復習，可以用文字語言、符號語言以及圖像來表征，這樣通過多種表征方式能夠促進學習者深刻理解增函數概念的本質，有利于培養學習者學會多角度、多方位、多種思路解決問題的習慣，在學習學科知識的同時，也可以進行美育的間接培養。

可視化技術通過將抽象的、復雜的知識或信息利用直觀的圖像或圖形呈現出來，以幫助學生快速地理解內容、發現規律、交流信息。高三數學可視化教學就是將抽象的數學學習對象（概念原理、結構關系、思想方法等）用可看見的表征形式（圖形、圖像、動畫等）清楚直白地呈現出來，使學生對數學學習對象有一個形象、直觀、整體的認識和理解。

最新的人教A版和人教B版高中數學教材中，以GGb軟件為載體，介紹了如何利用計算機技術實現數學功能，并開展相應的教學活動。所以教師需要主動學習，通過論文、書籍、豐富的在線資源學習，還可以通過社交群體、區域教研、公開課等方式進一步學習GGb，各級教育部門非常重視，一批優秀老師通過實踐取得了很好的成績，各種培訓推廣活動頗有成效。在高三數學教學中，平面幾何、函數、三角、立體幾何、解析幾何與GGb軟件的融合應用比較多，在概率統計上相對不足。同時我們還需要注意現在的學生本身GGb知識不足夠，而且暫時作為主體的參與度不高，學生只是感官上觀察、體會，所以在課堂教學中，我們不能唯“技術論”，用好GGb軟件這個輔助，全方位去提高課堂效率。

綜上所述，高三數學就是幾何、代數的組合體。在高三數學的學習當中，數形結合思想是學習數學的主要思想。GGb軟件幫助數學教師豐富教學方法，通過有效的教學促進學生對數學本質的理解。應用GGB軟件輔助高三數學教學，可以降低學習數學的難度，有利于培養學生的學習興趣，激發求知欲，給數學教學改革注入了新的活力。

參考文獻：

[1] 項俊.GGb軟件在高中數學教學中的應用探究[J] .上海中學數學，2019（4）：25-27.

[2] 彭淑琴.基于GGb的中學數學可視化研究[J] .陜西理工大學，2020.

[3] 劉怡軒.GGb在中學數學教學中的應用與展望[J] .中學數學教學參考，2021（5）.

3201501908274