聚焦核心素養 重視綜合實踐 提升數學閱讀

【摘 要】 近年來，數學中考越來越重視學生綜合能力的考察，也是大環境下中考命題的新趨勢.就2021年蘇州數學中考第27題而言，考察了三維空間中的注水追及問題，通過對該試題的分析與思考，提出初中數學教學應指向學生數學核心素養的發展、重視綜合實踐活動的價值、培養數學閱讀能力.

【關鍵詞】 數學核心素養;綜合與實踐;數學閱讀;中考數學

近年來，數學中考越來越關注學生綜合能力的考察，這是在重視素養發展背景下的命題趨勢.正如2021年蘇州數學中考的第27題，它推陳出新，舍棄了完全以動點為背景的數學綜合題，而是以向長方體容器中注水的水位變化問題替代.在此題中，繁瑣的過程說明讓學生望而卻步，仔細閱讀后發現，此題是披著注水問題外衣的追及問題，難度不大，但其指明了初中數學教學的育人方向.

1 試題呈現

2021年江蘇省蘇州市中考數學卷第27題：

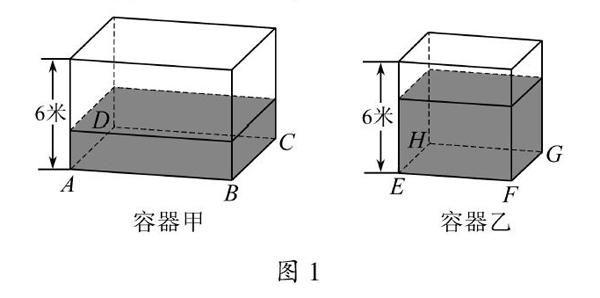
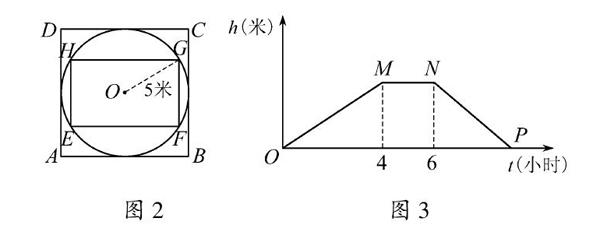
如圖1，甲、乙都是高為6米的長方體容器，容器甲的底面ABCD是正方形，容器乙的底面EFGH是矩形.如圖2，已知正方形ABCD與矩形EFGH滿足如下條件：正方形ABCD外切于一個半徑為5米的圓O，矩形EFGH內接于這個圓O，EF=2EH.

（1）求容器甲、乙的容積分別為多少立方米？

（2）現在我們分別向容器甲、乙同時持續注水（注水前兩個容器是空的），一開始注水流量均為25立方米/小時，4小時后，把容器甲的注水流量增加a立方米/小時，同時保持容器乙的注水流量不變，繼續注水2小時后，把容器甲的注水流量再一次增加50立方米/小時.同時容器乙的注水流量仍舊保持不變，直到兩個容器的水位高度相同，停止注水.在整個注水過程中，當注水時間為t時，我們把容器甲的水位高度記為h甲，容器乙的水位高度記為h乙，設h乙-h甲=h，已知h（米）關于注水時間t（小時）的函數圖象如圖3所示，其中MN平行于橫軸.根據圖中所給信息，解決下列問題：

①求a的值;

②求圖3中線段PN所在直線的解析式.

2 試題分析與思考

第一小問主要利用圓的相關知識及勾股定理求解.第二小問的含義是向兩個底不同的長方體容器中注水，對于容器乙而言，注水速度始終保持25立方米/小時不變，容器甲注水速度在前4個小時內保持25立方米/小時，而后速度增加a立方米/小時，即以（25+a）立方米/小時的速度注水，使得兩容器液面高度差始終一致，2小時后，繼續加快注水速度至（75+a）立方米/小時，直至兩容器液面相平.

就第二小問求解而言，難度不大，只需要抓住題目的兩個關鍵點，即：“兩容器液面高度差始終一致”和“兩容器液面相平”.對于“兩容器液面高度差始終一致”而言，就是一個巧妙的等量關系，學生可以在4到6小時內，任意選取兩個時間來表示兩容器液面的高度差，建立一個一元一次方程，進而得到a的值.而后“兩容器液面相平”更直白地呈現了一個等量關系，即點P橫坐標所對應的時間是甲、乙兩容器液面相等的時刻，進而又可以得到一個一元一次方程，求解出點P的具體坐標，再結合點N的坐標，可以很快得出線段PN所在的直線解析式.

追本溯源，此題就是一類三維的追及問題.在初中階段，學生更多接觸到的是二維追及問題.但此題推陳出新，在二維追及問題的基礎上加入了一個定量，即不同的底面積，將問題向三維的視角下推進，但究其本質，這類問題的解決方式是異曲同工的.

其實該試題并非聚焦于知識的考察，而是更關注學生在問題解決中數學素養與能力的體現.如：對于問題、圖象的理解與抽象就是最典型數學抽象能力的應用;構建高度差h與時間t的函數或者建立一元一次方程的過程就是數學建模素養的體現;還包括數學運算、直觀想象等素養的滲透.除了數學核心素養，像數學閱讀能力、數形結合思想也都能在該問題的解決中展現出來.

3 試題求解

問題（1）求解：易得容器甲底面邊長為10米;容器乙底面長為45米，寬為25米.故容器甲的容積是600立方米，容器乙的容積是240立方米.

問題（2）求解：①當t=4時，h=h乙-h甲=4×2540-4×25100=1.5，即M（4，1.5）.

又由于MN平行于橫軸，所以N（6，1.5）.

當t=6時，h=6×2540-4×25+2（25+a）100=1.5，解得a=37.5.

②解法一：方程思想.

設經過t1小時兩容器水位高度相同，可得25t140=25×4+62.5×2+112.5（t1-6）100，解得t1=9，即P（9，0）.

設線段PN所在直線的解析式為：h=kt+b.

將N（6，1.5）和P（9，0）代入h=kt+b，得到1.5=6k+b，0=9k+b.? 解得k=-12，b=92.

所以線段PN所在直線的解析式為：h=-12t+92.

解法二：“k”的實際意義.

設線段PN所在直線的解析式為：h=kt+b.

由題意：線段PN所在直線的解析式中k的實際含義是兩容器注水速度與其底面積比值之差，即k=2540-112.5100=-12.

因此，將N（6，1.5）代入h=-12t+b，得到1.5=-12×6+b，解得b=92.

所以線段PN所在直線的解析式為：h=-12t+92.

4 教學啟示

4.1 教學更應指向學生數學核心素養的發展

數學的學習一方面在于數學知識的掌握，另一方面指向數學核心素養的習得與發展.在立德樹人為教育根本任務的大背景下，數學核心素養培養更是如今教學的重中之重.近年來，數學中考越來越關注學生素養的考察.正如此題中，對于問題的理解并抽象出容器甲、乙的注水速度與水位變化的數學關系是對學生數學抽象能力的考察，如果學生數學抽象能力薄弱，根本不能提取出注水速度與水位的變化關系，那么更別去談求解此題.數學研究的對象就是源自于人類對于現實生活的抽象的東西，在此類基于現實背景的數學問題更注重數學抽象能力的考察.此外，在此題中，像h與t函數的構建、利用方程求解a的值，都是考察學生能否提煉出問題中的等量關系并用數學符號建立方程來表示，即數學建模素養.在數學模型的求解中，也涉及到數學運算等素養的考察.綜上所述，中考試題對于數學核心素養的考察是綜合性的，滲透于解題的各個環節之中.

數學核心素養的培養任重道遠，需要教師抓住契機、巧妙滲透、潛移默化.以數學抽象素養的培養為例，在數學學習中，數學概念是數學學科的“靈魂”，是中學數學教學的重點.數學概念在歷史的長河中沉淀，大多都擁有著豐富的歷史底蘊，其產生大多是數學抽象的結果.教師在概念教學的過程中，必然會引導學生觀察具體實物，提取本質屬性，抽象獲得概念，因此概念的教學是數學抽象素養培養的“溫床”.在初中階段，學生認知水平不高，所學習的數學內容相對淺顯，對于數學內容的表述大多停留于生活語言，而未上升至符號語言.所以，在初中階段存在的數學抽象大多是淺層次的，多數停留于半符號化階段.對此教師應重視數學抽象素養的培養，積極抓住適合培養數學抽象素養的數學概念，在概念的形成中體驗數學抽象的過程，滲透數學抽象的方法，并在課后練習和綜合實踐活動中鞏固與運用，多形式地發展學生的數學抽象能力.

4.2 重視綜合實踐活動的價值

“綜合與實踐”作為《義務教育數學課程標準（2011年版）》的一大特色與“數與代數”等并列為數學四大課程內容.“綜合與實踐”是以問題為載體、以學生自主參與為主的數學活動[1].該內容強調綜合性與實踐性，綜合性是指所研究問題廣泛、包含的數學知識全面、涉及的學科多樣、學生的素質綜合提升;實踐性強調學生在教師的引導下主動參與，體現“過程”.“綜合與實踐”是學生主動思考、積極探究、討論合作、實踐操作的重要平臺，也是創新精神與應用意識培養的重要載體.不妨深入思考該題，不難發現，此題的本質即為三維的追及問題.以此題為背景的九年級綜合實踐活動可以從二維追及問題出發，呈現如下的問題1，讓學生在熟悉的動點問題中探索函數解析式與具體問題之間的關系，為上述中考題的探究求解鋪墊.

問題1：如圖4，射線OM上有一點A，滿足OA=20cm，點P和點Q分別從點O和點A出發，沿OM方向，一開始均以1cm/s的速度勻速運動，4秒后，點P的速度增大acm/s，同時點Q速度不變，繼續運動2秒后，再次將點P的速度增大3cm/s，同時點Q速度不變，直到兩點相遇，運動停止.在運動過程中，當運動時間為t時，我們點P到點O的距離記為s1，點Q到點O的距離記為s2，設s2-s1=s.根據所給信息，解決下列問題：

（1）若a=1.5，嘗試繪制出s（cm）關于運動時間t（秒）的函數圖象.

（2）若s（cm）關于運動時間t（秒）的函數圖象如圖5所示，求a的值和線段EF所在直線的解析式.

思考：觀察線段DE和線段EF所在直線的解析式，兩條直線的“k”有什么實際含義？

問題1的第一小問旨在引導學生去讀題、提取關鍵的數學信息，進而讓學生在繪制出函數圖象的過程中，理解圖象上各個點的具體含義，積累數學抽象的經驗，也為第二小問提供解題思路.在學生自主探究完問題1后，教師可以給出問題2——2021年蘇州數學中考第27題，逐步引導學生從二維向三維飛躍.在問題2的解決中，教師可以指出兩個問題之間的聯系，并讓學生思考圖象中一次函數的“k”的具體含義，兩個問題中的“k”之間的差異在哪？學生通過對兩個問題的比較與分析，透過現象直擊問題本質，充分理解問題的內涵.

隨后，教師可以進一步激發學生思考：如果將正方體的容器換為其他立體圖形，如：圓柱、三棱錐等，水位高度的變化、注水速度與注水時間之間存在什么關系呢？如圖6所示，以正三棱錐OABC為例，已知其高為H米，△ABC的面積為S，注水速度為a立方米/秒，注水時間為t秒，水位高度記為h米，則可以得到h=H-3H3-3atH2S，

圖6若將正三棱錐OABC倒置，則可以得到h=33atH2S.雖然在三棱錐等錐形的幾何圖形中，水位高度會出現三次根號，不適合在考試中呈現，但是學生在探究的過程中，其數學建模、數學運算、直觀想象等數學素養得到了提升，也為今后高中的學習打下堅實的基礎.

4.3 擊破“畏難”心理，培養數學閱讀能力

數學閱讀能力是指學生能夠通過數學化的分析，從數學材料提取數學信息，形成自我的數學觀點.數學閱讀是一種內在的心理過程，需要經歷提取信息、數學建模和數學表達三個階段[2].對學生而言，題目越簡潔，越敢于去嘗試.但面對像該題數行的過程說明，以及考試限時的大環境下，學生難免會出現“畏難”心理，將題目的長短與問題的難易聯系起來，形成刻板印象，進而部分學生連題目都不愿意去閱讀.同時也有部分同學雖閱讀了題目，但其完全沒有理解題目的含義，究其原因，一方面，可能是學生自身的數學知識水平還未達標，另一方面，可能歸咎于數學閱讀能力的薄弱，無法提取關鍵信息服務于問題的解決.

因此，在日常教學中，教師首先要打破學生的刻板印象，將其頭腦中“怕麻煩”“不想做”等惰性思維扼殺，讓學生形成不畏難、不退縮、不妥協的學習品質，在遇到諸如此類題目時，不怕困難，敢于去讀題嘗試.而后，教師應該教會學生數學閱讀的方法，讓學生在教師的指導下，能夠完全提取出題目中所給的有效條件，并在完備的知識體系下，快速地挖掘出各個條件所帶來利于解題的新條件.教師在問題的分析中，應多讓學生思考“題目中有什么條件”“這些條件能得到什么新條件”“新舊條件中有哪些是利于解題的”等問題，促使學生在會解題的基礎上，促進理解題目的內涵、形成自己的解題方法、獲得自身能力與素養的全面發展.

參考文獻

[1]中華人民共和國教育部制定.義務教育數學課程標準（2011年版）[M].北京：北京師范大學出版社，2012：5.

[2]孫俊勇.談數學閱讀[J].基礎教育課程，2020（2）：42-46.

作者簡介

黃賢明（1999—），男，江蘇蘇州人，中學二級教師，研究方向：初中數學教學研究.