問題導向的初三數學復習課

胡生兵 李洪兵

【摘 要】 國培期間數學特級教師展示了一堂初三數學復習觀摩課，課題是“二次函數的綜合應用”，本節課起于一個主題干，成于八個追問.本節課展示問題由封閉到開放，探究性強，教學價值高，是一節成功的復習課，充分體現了以下特點：高處立意，踐行課改理念;問題驅動，夯實學習過程;指向評價，落實數學素養.【關鍵詞】 二次函數;綜合應用;教學實錄;教學評析

二次函數的綜合應用是初中數學的重點，是學生學習的難點，是中考的熱點.“二次函數的的綜合應用”是初三復習的重要內容，不少老師往往采取題海戰術進行復習，但特級教師姜老師的教學卻另辟蹊徑——起于一個主題干，八個追問螺旋上升層層遞進，對二次函數作了全面復習，并取得了較好的效果.本文對該堂課的主要內容進行了實錄，并對幾位教研員和專家們的點評作了實錄和分析.

1 基本情況

1.1 授課對象

教學對象是重慶A中學（重慶市重點中學）的初三學生，該班學生思維活躍，善于思考，積極主動.該班總成績位于年級前列.

1.2 學情分析

本節課內容是參照人教版初中數學內容設計.作為復習課，學生已經學習了勾股定理，二次函數的定義、圖象及性質等基礎知識，但學生不能靈活運用所學知識.在前期的學習中，學生已經掌握了研究函數的方法，對函數思想、數形結合思想已有初步認識，但依然缺乏解決數學綜合問題的思維方法，并且分析問題和解決問題的能力還有待提高.因此本節課旨在鞏固與二次函數相關的知識，強化數形結合、類比、轉化、待定系數法、反證法等數學思維方法，提高“四能”.

1.3 例題設計

已知一次函數的圖象經過A（0，2）、B（4，6）兩點，完成下面的問題：

（1）求過A、B兩點的一次函數解析式;

（2）已知一個二次函數圖象經過點A，B和點D（1，0），求該函數解析式并畫出函數圖象;

（3）利用函數圖象寫出方程x2-3x+2=x+2的解和不等式x2-3x+2>x+2的解集;

（4）求△ABO的面積;

（5）求△ABD的面積;

（6）若點G是直線AB下方拋物線上的一點，當△ABG面積最大時，求點G的坐標;

（7）在x軸上是否存在點M，使M，A，B三點構成的三角形是直角三角形？若存在，求出點M的坐標;若不存在，請說明理由;

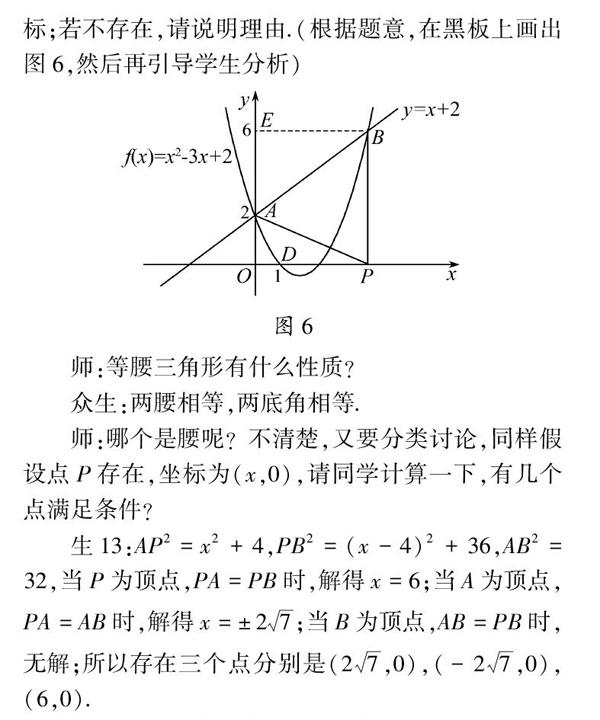
（8）在x軸上是否存在點P，使P，A，B三點構成的三角形是等腰三角形？若存在，求出點P的坐標;若不存在，請說明理由.

意圖探析 以問題為主線，體現問題是數學的心臟，問題是教學的心臟，問題是學生認知的心臟，展示問題驅動式教學模式[1].遵循學生的認知規律，設計由淺入深、由易到難、結構簡單、邏輯聯系、前后鋪墊的問題串，形成學習任務，通過這些問題的解決，鞏固二次函數的基本性質、解一元二次方程、解三角形面積等基礎知識，幫助學生掌握解決二次函數問題的基本方法，比如待定系數法、反證法、數形結合、割補法等.通過解決開放型問題和一題多解，培養學生的發散思維和創造能力.

2 課堂實錄

2.1 復習回顧，引入新課

師：同學們現在已經學習了哪些函數？

眾生：一次函數、反比例函數、二次函數.

師：它們的圖象是怎樣的呢？

眾生：一次函數圖象是直線、反比例函數圖象是雙曲線、二次函數圖象是拋物線.

師：很好，今天我們將學習二次函數的綜合應用.

（教師板書課題，展示問題）

評析 通過回顧，使學生集中注意力，激發學生的學習興趣，為后續學習做鋪墊，同時拉近師生之間的距離.

2.2 分析問題，解決問題

問題1 求過A，B兩點的一次函數解析式.

師：我們怎么求一次函數的解析式？

生1：設一次函數的解析式為y=kx+b，然后將點代入，從而求出k，b.

教師：非常好，前面知識掌握不錯，大家現在求解一下（停頓一會），同學們求出來沒有？

生2：一次函數解析式為y=x+2.

師：很好，大家會求一次函數解析式，那二次函數解析式呢？大家思考下面這個問題.

問題2 已知一個二次函數的圖象經過點A，B和點D（1，0），求該函數解析式并畫出函數圖象.

師：請同學們思考怎么求此解析式？

生2：設二次函數的解析式為y=ax2+bx+c，然后將A，B，D三點的坐標代入，得到方程組，從而解得a=1，b=-3，c=2，進而y=x2-3x+2.

師：很好，這個解題過程可以簡化嗎？或者說解析式可以設成其他形式嗎？

生3：根據已知條件知，拋物線與y軸的截距為2，所以設解析式為y=ax2+bx+2.

師：非常好，對二次函數的系數理解很深刻.那同學們現在描點，找到對稱軸和頂點，畫出二次函數的圖象.

評析 函數解析式是研究函數的基礎，問題由簡單到復雜符合學生的認知規律，通過簡單問題的成功解決，使學生獲得成功感，激發學習動力.此問題的解決方法是待定系數法，該方法不僅在初中很重要，在高中解決解析幾何問題也常用，強化學生的思維方法，為后續學習打基礎.

問題3 利用函數圖象寫出方程x2-3x+2=x+2的解和不等式x2-3x+2>x+2的解集.

師：根據圖1可知，一次函數圖象有兩個交點，那這兩個交點代表什么意思？

生4：代表這兩個函數的自變量取交點橫坐標時，所對應的函數值相等.

師：很好，那方程的解為多少？

生4：方程的解為0或4.

師：非常好，那不等式的解集？

生5：因為是二次函數值大于一次函數值，所以是二次函數圖象在一次函數圖象上方所對應的自變量x，所以不等式的解集為x<0或x>4.

評析 運用數學結合解一元二次方程，為解不等式作鋪墊，強化學生的數學結合思想.通過數形結合幫助學生理解方程與函數、方程與不等式、函數與不等式之間的聯系，此問題還為高中學習函數零點打下堅實基礎，充分體現了教學的彈性.

問題4 求△ABO的面積.

師：同學們能否在圖中找到三角形△ABO？能口算出三角形面積嗎？

眾生：能，面積為4.

師：為什么？

眾生：如圖2，因為底OA為2，高為4，所以面積為4.

師：還有其他方法嗎，同學們下去還可以再探究.

評析 面積是幾何中最基本的問題，解決此問題的關鍵是尋找底和高.運用數形結合思想，尋找解題方法，有助于培養學生觀察、分析和解決問題的能力，為下一個問題作鋪墊.

問題5 求△ABD的面積.

師：求解思路是什么？

生6：如圖3所示，過點D作y的平行線交AB于點F，則S△ABD=S△ADF+S△DBF=12DF·OC，而DF=1+2=3，OC=4，所以S△ABD=6.

生7：如圖3，連接OB，則S△ABD=S△AOB+S△DOB-S△ADO.

生8：如圖3，過點B做垂線交x軸于點C，則S△ABD=SABCO-S△ADO-S△BCD.

生9：如圖3，延長BD交y軸于點H，則S△ABD=S△ABH-S△ADH.

師：方法靈活，但所有方法體現的是“割”與“補”的思想.

評析 問題簡潔，難度不大，學生易理解題意，從而重心放在分析問題上.此問題解題方法靈活，生7和生8的方法是學生所熟知，而生6的方法學生不易想到，但能簡化求解過程，體現了多想少算的理念，所有方法體現的思想是“割”或“補”.通過一題多解，展示不同水平學生的思維，提高學生的學習興趣，培養學生的發散思維和優化思想.

問題6 （思考題）若點G是直線AB下方拋物線上的一點，當△ABG面積最大時，求點G的坐標.

師：求三角形面積，需要去確定三角形的底和高，說說你們的思路？

生8：如圖4所示，過點G作y的平行線交AB于點F，以FG為底，則根據問題5可知△ABG的高為定值4，所以只需要FG最大即可.設G點坐標為（x，x2-3x+2），則FG=x+2-（x2-3x+2）=-x2+4x（0

師：通過類比尋找變與不變.

生9：以AB為底，則△ABG的高為點G到直線AB的距離.根據已知可得AB=42.而根據點到直線的距離公式可得h=x（4-x）2（0

師：很好，學習能力很強.點到直線距離公式初中不學，到高中才學，很多同學都不知道，感興趣的同學可以去推導一下.大家還有其他方法？生9你不用點到直線的距離公式能解決這個問題嗎？（學生保持沉默）

師：沒關系，我們一起來思考，其實當以AB為底時，我們相當于在拋物線下方去尋找距離直線最遠的點，根據圖象可以感知，移動直線AB與拋物線相切，則切點就是要找的那個點.而相切時，判別式等于零，從而解出直線方程，進而求得交點.

評析 此問題難度大，教師將其改成思考題，重點分析思路，提供了不同思維難度的方法供大家思考，體現了因材施教，分層教學的理念.此問題的解題方法有切線法，代數法，蘊含了類比和數形結合的思想，使不同學生得到不同的展示和發展，培養了學生敢于挑戰的意志品質.

2.3 引發探究，深度學習

問題7 在x軸上是否存在點M，使M，A，B三點構成的三角形是直角三角形？若存在，求出點M的坐標;若不存在，請說明理由.（根據題意，在黑板上畫出圖5，然后再引導學生分析）

師：根據勾股定理有：兩直角邊的平方和等于斜邊的平方，這是一個充要條件.那我們現在知道哪個角是直角？

眾生：不知道.

師：從而我們要采用什么方法？

眾生：分類討論.

師：那先假設點M存在，并設為（x，0），大家現在求解一下，看有幾個點滿足條件.

生9：以點A為直角頂點時，則AM2+AB2=MB2，而AM2=x2+4，AB2=32，BM2=（4-x）2+36，所以解得x=2;同理當以點M為直角頂點時，無解;當以點B為直角頂點時，解得x=10，綜上存在兩個點滿足條件，即（10，0）或（2，0）.

師：大家繼續思考，當以點A為直角頂點時，還有別的方法計算點M的坐標？

生10：過點A作AB的垂線交x軸于點M，因為kAM·kAB=-1，kAB=1，A（0，2），從而可以求出直線AM的解析式，進而求得點M的坐標.

師：很好，這樣是可行的，但是你知道為什么直線相互垂直時斜率乘積等于-1？

生11：不知道，我記的結論.

師：很誠實，因為那是高中才學的，但是如果你感興趣可以課后推導一下.其他同學還有別的方法？

生12：有，當以點A為直角頂點時，△ABE為等腰直角三角形，從而△AOM也為等腰直角三角形，從而OM=OA=2，即點M坐標為（2，0）.

師：很好，觀察非常仔細，磨刀不誤砍材工，做題不要急動筆，先想透徹，再書寫，能提高解題效率.

問題8 在x軸上是否存在點P，使P，A，B三點構成的三角形是等腰三角形？若存在，求出點P的坐標;若不存在，請說明理由.（根據題意，在黑板上畫出圖6，然后再引導學生分析）

師：等腰三角形有什么性質？

眾生：兩腰相等，兩底角相等.

師：哪個是腰呢？不清楚，又要分類討論，同樣假設點P存在，坐標為（x，0），請同學計算一下，有幾個點滿足條件？

生13：AP2=x2+4，PB2=（x-4）2+36，AB2=32，當P為頂點，PA=PB時，解得x=6;當A為頂點，PA=AB時，解得x=±27;當B為頂點，AB=PB時，無解;所以存在三個點分別是（27，0），（-27，0），（6，0）.

師：非常好，此問題類似于問題7，都是列等式，解方程.問題7和問題8都是存在型問題，我們均假設存在，然后驗證，歸結起來都是采用了反證法，大家下去好好體會.

評析 問題7、8均屬于開放型問題，有助于培養學生的創造思維.牛頓曾說：“反證法是數學家最精良的武器之一.”[2]反證法在高中、大學中都是非常重要的，能提解題效率.此類題的解題思路都是先假設成立，然后去驗證，本質都是采用的反證法.這兩個問題的解決過程很好的體現了數與形之間的統一，展示了數學的統一美，強化了數形結合思想.

2.4 歸納總結，反思升華

師：學習了哪些知識？

眾生：一次函數，二次函數，二次方程，二次不等式，二次函數的最值.

師：運用了哪些方法呢？

生：代數法，幾何法，數形結合，反證法.

師：學習了本節課你們有什么體會呢？

生14：對一個問題可以多角度解決.

生15：對于存在型問題，先假設存在，然后去驗證.

評析 歸納總結有利于開發元認知，有利于學生建構知識網絡，促進學生數學思維的發展[1].教學中，學生是主體，要充分了解學生，讓學生表達，培養學生的表達能力.

2.5 課后練習，鞏固提高（略）

3 教學評析

通過教學觀摩，教研員和專家們對本節課評價很高.本節課的特點是以問題為主線，形成知識鏈，構成學習任務.問題結構簡單，難度由淺入深.問題類型由封閉型到開放型，探究性強，教學價值高，是一節成功的復習課，具體體現在以下幾個方面：

3.1 高處立意，踐行課改理念

從教學理念來看，本節課體現了新課標教學理念.教師讓學生先思考，小組討論，上臺展示，再追問，體現了以學生為主體，教師為主導和數學教學是數學活動的教學理念.本節課學習的知識由淺入深，解決問題方法，蘊含許多常用的數學思想，體現了深度教學理念.

3.2 問題驅動，夯實學習過程

從教學過程來看，教師圍繞問題而教，學生圍繞問題而學，體現了問題是數學的心臟，問題是教學的心臟，問題是學生認知的心臟[3].數學從某種角度來講是由問題構成的，沒有問題，就沒有數學，學生認知的是問題，思考的是問題，問題是思維的土壤.沒有問題，就缺乏思維的土壤，也就難以思維，學生也就不能發現問題、提出問題、分析問題、解決問題.本節課是一堂高水平的解題教學課，通過有限道題的解題方法、解題策略、解題思想，去領悟解決無窮道題的智慧.

3.3 指向評價，落實數學素養

從教學效果來看，本節課充分體現了真、善、美，充分發展了學生的數學素養.首先課堂很真，在上課之前，教師沒有與學生進行任何溝通.問題很真，這些題目由淺入深，完全是經過精心的設計，并且這些題目是平常教學和中考中經常遇見的題目.該課有助于應試也是真的，但這節課也是科學的探究，以問題為載體，引導學生思考方法，促進知識自然生長，是一堂非常有數學味的課.善體現在教學方法和處理問題方法不斷改進的過程中，教師特別強調“你先說說你的思路和方法”，算完之后老師又提問“還有沒有別的方法”，體現了等一等，問一問的教學思想，充分展示了心中有學生，給學生提供展示的機會.本節課呈現了課件的簡潔美、問題的邏輯美、數形的統一美.

參考文獻

[1]徐娟.一堂基于深度理解的二次函數綜合復習課[J].中學數學，2020（22）：27-29.

[2]王滟林，熊露，趙思林.反證法的教育價值與教學建議[J].中學數學，2019（23）：86-88.

[3]潘龍生.教學，少些一帶而過[J].數學通報，2015，54（01）：14-16.

作者簡介 胡生兵（1993—），男，四川廣安人，碩士，主要從事中學數學解題和教學研究.發表論文6篇，出版專著1本.

李洪兵（1973—），男，重慶璧山人，中學正高級教師，重慶市特級教師，重慶市學科帶頭人，重慶市學科名師.