對初中數學核心素養的理解與課堂落地的途徑

蘇海鵬

【摘要】數學核心素養是指學生通過數學學習而具備的正確價值觀、關鍵能力與必備品質，是數學學科育人價值的集中體現.因初中屬于義務教育階段末端，數學知識深度、廣度、難度、復雜度具備一定的層次特征，因此，對初中數學核心素養的理解要綜合教材內容、學生特點、學習場域等因素綜合展開，并遵循初中數學課堂教學措施的一般規律，這樣有利于核心素養的落地.本文從三個維度理解初中數學核心素養的內涵，提出可行的課堂落地途徑，以供教者學習借鑒.

【關鍵詞】初中數學;核心素養;理解維度;落地途徑

一、初中數學核心素養的三個理解維度

現階段，具有明確概念界定及內涵設計的數學學科核心素養，基本都是源于《普通高中數學課程標準（2017年版）》（以下簡稱：《高中標準》）提出的六種核心素養或對這六種核心素養的擴展、衍化.而《義務教育數學課程標準（2011年版）》（以下簡稱：《初中標準》）中并沒有明確給出核心素養內容，機械套用容易造成對初中數學核心素養理解的泛化與無序.但值得注意的是，《高中標準》提及“核心素養”時，是從數學學科這一角度出發的，并沒有明確限定六種核心素養必須納入高中數學的范疇，換言之，這六種核心素養在初中數學階段仍然具有適用性，只是身為初中數學教師，在理解核心素養時，要兼顧《初中標準》提出的相關要求.具體來說可劃分為三個理解維度.

（一）課程內容維度

《初中標準》的“（三）課程內容”從各學段出發，對初中數學知識體系進行了詳細梳理，基于“數與代數”“圖形與幾何”“統計與概率”“綜合與實踐”四方面課程內容，提煉出初中階段數學日常教學應側重的“十種能力”，分別為數感、符號意識、空間觀念、幾何直觀、運算能力、推理能力、模型思想、數據分析觀念、應用意識及創新意識，而這十種能力與《高中標準》中提出的“六大核心素養”存在一定的重合性、相似性，如《高中標準》中提及的“數據分析”與《初中標準》中的“數據分析觀念”基本一致，因此，可以將這“十種能力”視為初中數學的“十大核心素養”.

（二）課程目標維度

《初中標準》的“第二部分 課程目標”中強調，學生通過數學學習應該達到“四基”“四能”“一意識”的目標，這也是理解初中數學核心素養的科學維度.其中，“四基”所強調的基礎知識、基本技能、基本思想、基本活動經驗可以覆蓋“十種能力”中的前八種，進而與《高中標準》提出的六種數學核心素養建立協同關系.“四能”所強調的發現、提出、分析、解決問題的能力，對應《高中標準》中提出的“應用意識”.而“一意識”，即“初步的創新意識”，它的形成有賴于數學興趣激活、數學信心塑造、數學習慣養成，對應《高中標準》中提出的“創新意識”.

（三）“三會”理解維度

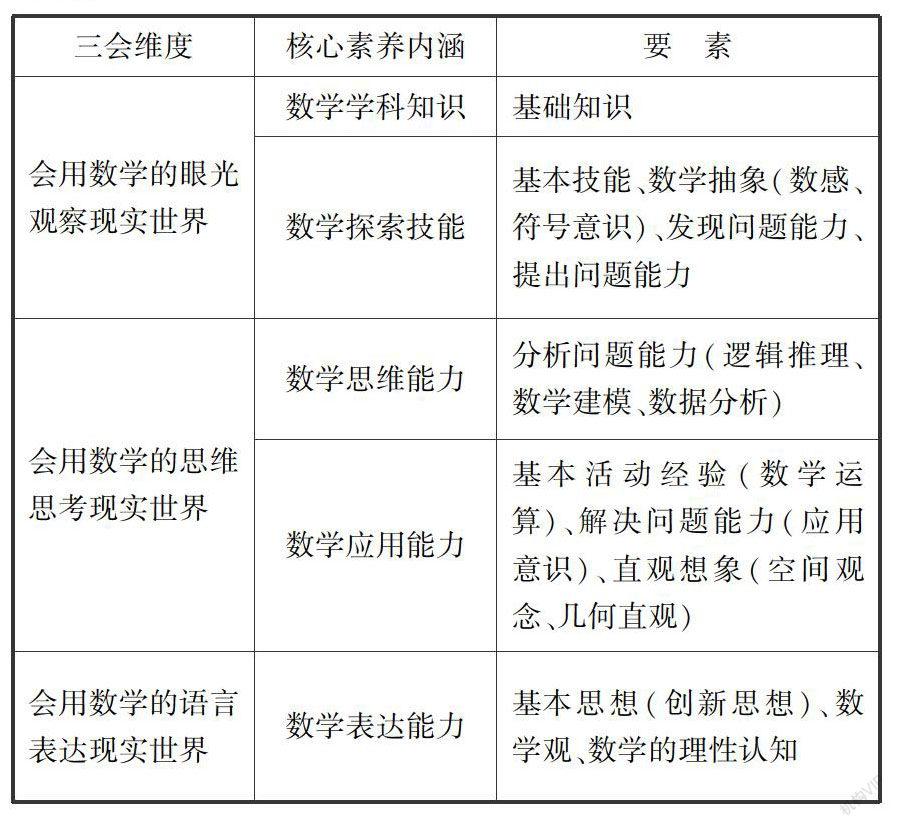
“三會”是近年來義務教育階段對數學課程教學提出的新要求，其本身內涵也是對初中數學核心素養的一種理解方式.所謂“三會”，即會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界.很明顯，“三會”所提的要求超出了初中數學課程教學目標，且并不局限于學生數學能力的當前發展，更注重數學實踐對現實世界的作用，這與《中國學生發展核心素養》的主旨是高度一致的.同時，“三會”中的“觀察現實世界”可以對應“四能”中發現、提出問題的能力，而“思考現實世界”可以對應“四能”中分析問題的能力，“表達現實世界”可以對應“四能”中解決問題的能力.基于“三會”與“四能”之間的密切聯系，可見二者保持著高度統一性.

二、初中數學核心素養的課堂落地途徑

以《高中標準》明確提出的數學“六大核心素養”為基礎，初中數學視域下，無論是“十種能力”“四基”“四能”“三會”，都可以找出與其密切的關系，同時存在自身核心素養的特殊性.因此，在設計初中數學核心素養的課堂落地途徑時，教師應該秉承系統性、兼容性、協同性思維，以更全面地體現初中數學核心素養價值.其中，系統性是指保障“十種能力”“四基”“四能”“三會”的完整性，而兼容性是指不同核心素養理解維度下理念的相互滲透、方法的相互借鑒，協同性則強調“一意識”要始終貫穿教學過程.為了便于設計初中數學核心素養的課堂落地途徑，本文將其重新整合，把各種理解維度下重復、同質的部分進行合并，最終落腳點是“三會”.

（一）基于“觀世界”構建初中數學核心素養的課堂落地途徑

學會用數學視角去觀察現實世界，這是核心素養落地的第一步.學生需要必要的數學基礎知識去理解現實現象、問題、假設等，進而才能借助一系列數學符號去發現問題、提出問題.以人教版八年級下冊第十七章“勾股定理”為例，教師在進行新課教授的過程中，要想促進核心素養課堂落地，“觀察現實世界”是一個很不錯的途徑.例如，借鑒教材中的“地磚”案例，教師可以在課堂上創設更富有現實代入感的情境，利用PPT展示生活中常見的正方形瓷磚或Excel表格，引導學生利用已掌握的基礎知識展開分析，直到引出“a2+b2=c2”的勾股定理公式.值得注意的是，基于驗證性思維進行的教學活動，情境創設素材僅僅是佐證工具，學生并非從“觀察到的”去推導“未知”，而是根據“已知”（勾股定理）去強行地驗證其正確性，這種方式是難以促使核心素養落地的.教師需要用一系列的步驟（如“問題導向”）啟發學生，建立現實世界觀察過程中的數學價值呈現機制.

問題導向實踐機制如下：

（1）圖像展示的是什么？（預設答案：瓷磚）

（2）瓷磚是怎樣的形狀？（預設答案：正方形）

（3）正方形有哪些特點？（預設答案：邊長一樣）

（4）紅框內一共有多少塊？（預設答案：100，強調用邊長平方求解）

（5）假設每個瓷磚邊長為a，你能分別計算出三個直角三角形的面積嗎？（預設答案：4a2，9a2，直角三角形輪空）

（6）下面我們一起來計算這個直角三角形的面積.（利用圖像拼接的方法）