思維可視化視角下問題解決型作業的設計研究

徐建

摘要：高中數學的作業主要由問題解決型作業組成，學生作業答案很多時候不能體現其思維過程，導致教師對其反饋不夠精確，借助思維導圖這個工具培養學生元認知的策略及數學思維可視化的手段，從而形成問題解決型作業練習的基本框架，為學生數學思維可視化打下基礎。本文選擇以幾何圖形為載體的應用題為例來進行具體的案例設計研究。

關鍵詞：思維可視化;問題解決;思維導圖

中圖分類號：G633.63 文獻標識碼：A文章編號：1992-7711（2021）07-085

一、研究背景

當前高中數學教學的難點在于知識多、深、繁、難，且知識的獨立性大且較為抽象，這需要學生進行思維理解，而理解就是需要學生對知識進行思維加工，將其內化并建構為自己的知識體系。而高中數學的作業也偏向于問題解決型作業，學生的答案很多時候不能反映其思維，導致教師對其反饋及評價過于籠統，無法進行個人針對性反饋，這樣的作業效果要打上折扣。因此，傳統問題解決型作業需要考慮設計一些環節將學生的思維過程可視化，既利于教師了解學生個性的學習情況，也利于學生進行自我訂正，從而實現作業效果的正反饋。

二、理論依據

思維可視化要想在數學問題解決型作業中能夠順利實施，需要借助以下理論及實施工具：

1.元認知提供數學思維可視化的需求

元認知是對自身認知過程的一種認知，匈菲爾德在討論元認知對于數學問題解決的影響時，涉及以下三個涵蓋的元認知成分：（1）個體對自己的認知特點的認知;（2）個體的自我調節程序，包括對認知過程的監督和“即時”作出決策;（3）個體對認知過程的反思和評價[1]。

學生在進行應用數學概念進行數學問題解決時，形成了各種控制和認知過程，而思維可視化在數學問題解決型作業中體現的恰好就是這樣的功能，一開始采用較為直接的策略與告知講解，使得學生充分了解這樣的策略，體驗到策略對其作業表現的促進作用，使其能夠在日后的數學學習及作業中主動運用所習的策略知識。

2.思維導圖提供數學思維可視化的支撐

思維可視化就是把學習過程中的思考方法和思考路徑通過圖示技術呈現出來[2]。知識可視化就是采用概念圖、結構圖等手段將數學知識構建成互相連通的體系。東尼·博贊發明的思維導圖的主要要素包括中心節點、分支節、點、連線、注釋和一些輔助信息。它將信息作為主題或者子主題，應用多樣的顏色來呈現，加強了視覺沖擊。因此，思維導圖作為個性化的圖示表示方式，能夠有效溝通數學知識可視化和思維可視化，成為思維可視化的核心技術。

3.問題解決提供數學作業可視化的框架

美國教育學家G·波利亞在他的著作《怎樣解題：數學思維的新方法》這一本書中提出“解題表”，他具體歸結為四個階段：第一，我們必須理解改題目，我們必須清楚地看到所要求的是什么。第二，我們必須了解各個項目是如何相關的，未知量和數據之間有什么關系，以得到解題的思路，擬定一個方案。第三，我們執行我們的方案。第四，我們回顧所完成的解答，檢查和討論它。[3]

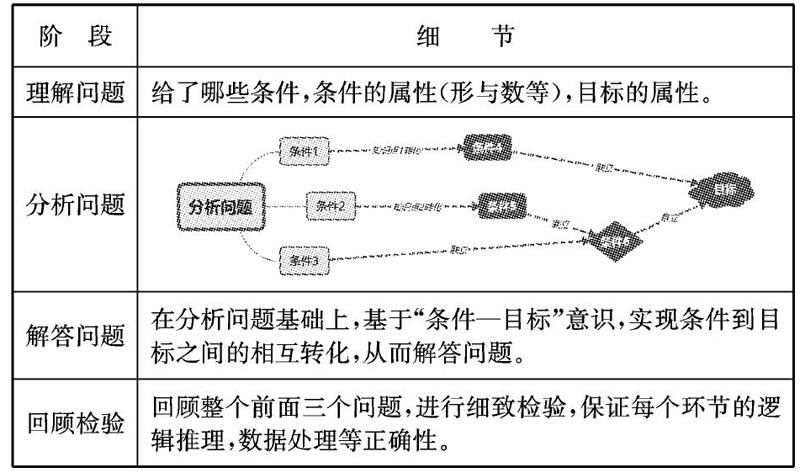
這里將數學問題解決分為四個階段：理解問題—分析問題—解答問題—回顧檢驗，并且將每個階段所做的事進行集中說明：

波利亞的解題表正好搭建了數學作業可視化的框架，為數學作業的可視化打下堅實基礎。

三、設計框架

傳統數學問題解決型作業的可視化設計可以某一塊內容的可視化作業設計作載體，研究可視化作業設計過程的一般流程，并在此基礎上，將一般流程運用于高中數學其他內容的作業設計中，得到各章節可視化作業設計的具體案例。本篇主要以幾何圖形為載體的應用題為例進行說明。

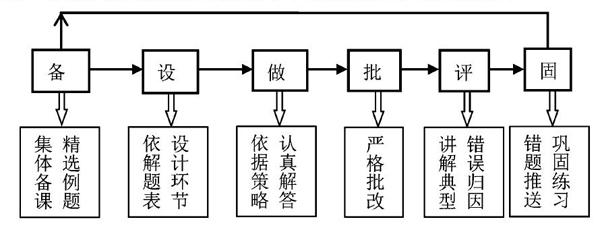
設計可視化作業的目的是讓教師更加關注學生的內隱的思維過程，了解學生利用數學理論和方法去分析和解決問題的全過程。可視化作業設計的過程中，可按照以下流程進行：

“備”：教師之間先進行集體備課，準備能夠展現學生思維水平的問題解決型作業;

“設”：教師依照解題表，設計作業問題解決的各個環節，例如審題時，規定學生將數據和限制性條件可視化（列表、示意圖等手段），解答時，要求學生用思維導圖說明解題思路，強調思路的簡潔性，方便教師的批閱;

“做”：學生認真按照教師的“設”進行問題解決作業的練習;

“批”：教師針對學生的“做”進行批改，重點在于指明學生思維誤區;

“評”：師生共同參與下，教師講解題目的典型錯誤，指明學生思維上誤區，后續讓學生自己進行錯因分析，提高其學習的自主性;

“固”：學生在教師提供的錯題推送后進行鞏固練習。

四、具體應用

應用題是培養學生數學建模能力的有效載體，其解決過程為：實際問題轉化為數學問題數學問題的求解數學解答回歸實際問題，關鍵是將實際問題轉化為數學問題。

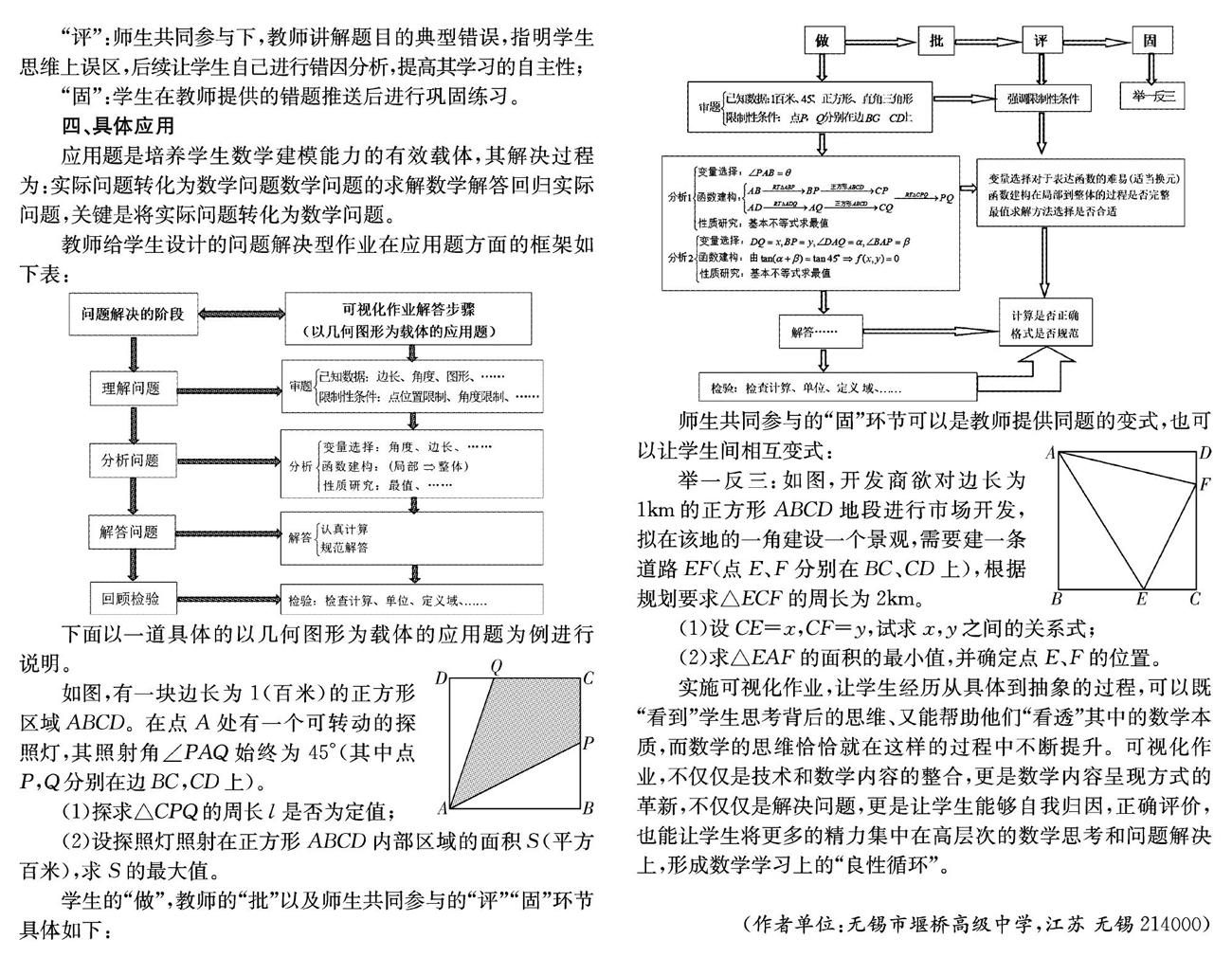
教師給學生設計的問題解決型作業在應用題方面的框架如下表：

下面以一道具體的以幾何圖形為載體的應用題為例進行說明。

如圖，有一塊邊長為1（百米）的正方形區域ABCD。在點A處有一個可轉動的探照燈，其照射角∠PAQ始終為45°（其中點P，Q分別在邊BC，CD上）。

（1）探求△CPQ的周長l是否為定值;

（2）設探照燈照射在正方形ABCD內部區域的面積S（平方百米），求S的最大值。

學生的“做”，教師的“批”以及師生共同參與的“評”“固”環節具體如下：

師生共同參與的“固”環節可以是教師提供同題的變式，也可以讓學生間相互變式：

舉一反三：如圖，開發商欲對邊長為1km的正方形ABCD地段進行市場開發，擬在該地的一角建設一個景觀，需要建一條道路EF（點E、F分別在BC、CD上），根據規劃要求△ECF的周長為2km。

（1）設CE=x，CF=y，試求x，y之間的關系式;

（2）求△EAF的面積的最小值，并確定點E、F的位置。

實施可視化作業，讓學生經歷從具體到抽象的過程，可以既“看到”學生思考背后的思維、又能幫助他們“看透”其中的數學本質，而數學的思維恰恰就在這樣的過程中不斷提升。可視化作業，不僅僅是技術和數學內容的整合，更是數學內容呈現方式的革新，不僅僅是解決問題，更是讓學生能夠自我歸因，正確評價，也能讓學生將更多的精力集中在高層次的數學思考和問題解決上，形成數學學習上的“良性循環”。

（作者單位：無錫市堰橋高級中學，江蘇 無錫214000）