對高一數(shù)學學困轉化的思考

劉曦文 吳林炎

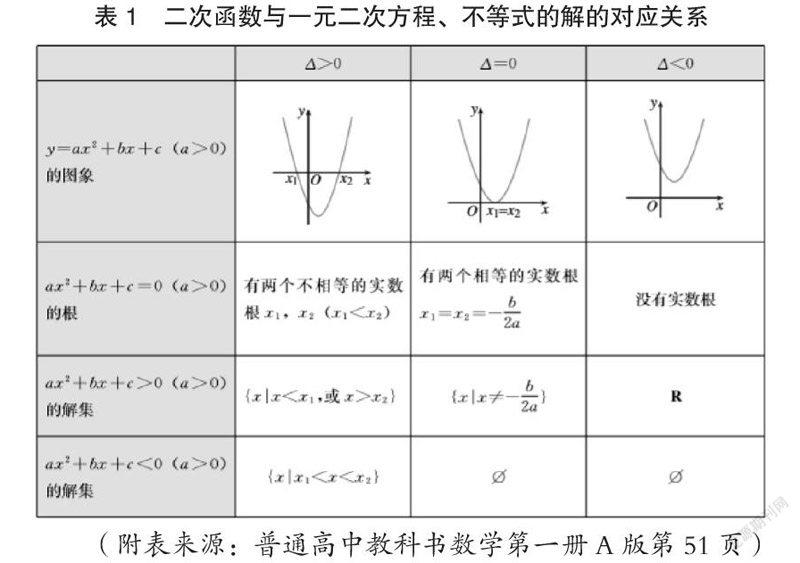
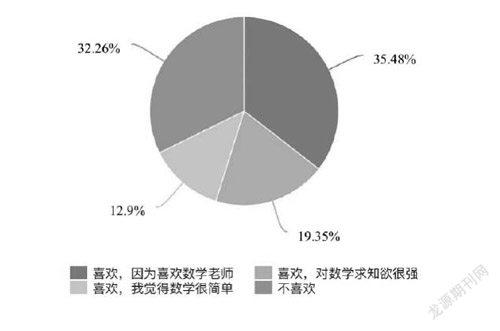
摘 要：本文主要是分析了高一學生數(shù)學學習困難的原因，以及結合高一教學提出幾個相應措施，講述教師從哪些方面提高高一學生的數(shù)學成績。

關鍵詞：高一學生;數(shù)學學習;學習興趣

提起數(shù)學，“難”這個字是首當其沖的，和小學、中學相比，高中數(shù)學的學習確實是不容易的，不僅要投入時間，還要思考，而事實上，在高中努力了，但成績依舊不理想的學生大有人在。高一正是中學結束邁入高中的過渡階段，當他們滿懷憧憬、信心滿滿地開始高中的學習，經(jīng)過一段時間學習，抽象和枯燥的感覺油然而生，數(shù)學學習困難的問題逐漸體現(xiàn)，從而開始對數(shù)學產(chǎn)生不自信，甚至是畏懼心理，也嚴重影響數(shù)學成績的提高。高一作為高中學習的開始階段，對整個高中的學習影響是巨大的。數(shù)學和其他科目不一樣，知識環(huán)環(huán)相扣，很多高一的概念和思想在整個高中都是不可或缺的。

在高一樹立信心，可以促進之后二年的學習;同樣的，如果高一學習遇到了瓶頸，那么對往后學習的阻礙也是不容忽視的。

一、高一學生數(shù)學學習困難形成的原因

（一）學生心理不成熟

高一學生一般是十六歲，或十七歲，這正是青春期、叛逆期。這個時期的孩子心智不成熟，自我控制能力差，高中學習不同于中學學習，高中注重的是主動學習，積極思考，科學的學習計劃，中學往往是學生圍著教師轉。在高中，則需要自我把控時間，把中學學習六科的時間分配到現(xiàn)在的九科，很多學生不能做到時間和科目上很好的平衡，導致學習效率低，學得苦卻學不好。……