把握課堂“意外”,提高思維層次

浙江省杭州第十四中學(310006) 樓思遠 周 艷

近日,筆者在課堂上講解一道關于二次曲線的切線問題時,學生提出了異議,在加以簡單的幾何解釋后學生仍有疑問,于是師生約定:各自思考后,第二天課堂展示成果,分享思路與比較哪種方法更優.根據學生展示的不同方法,師生一起通過討論分析將其整合與歸類.接著,筆者又依次給出幾道不同梯度的相關問題讓學生完成,最終取得了較好的教學效果,過程如下:

1 突發“意外”,順水推舟

課堂教學片段:

題目:已知拋物線C1:y=x2+2x和C2:y=-x2+a,若直線l同時是C1和C2的切線,則稱l是C1和C2的公切線,問:當a取什么值時,C1和C2有且僅有一條公切線?試寫出公切線的方程.

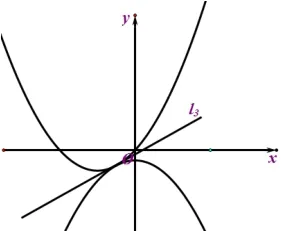
圖一

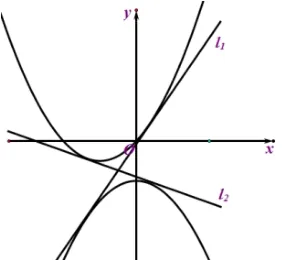
圖二

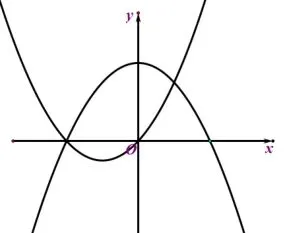
圖三

師:顯然,由題可知圖象應該如此(黑板上畫出圖一),從而列出方程解得答案.

生1:老師我認為圖象往下移一點(圖二)也只有一條切線l1.

師:(略微一愣,微笑的畫出了另一條切線l2),從圖象可以看出這種情況有兩條切線.

生2:那如果向上移動呢,是不是也是兩條?

師:(在黑板上作出圖三)因為開口大小的關系,從圖象可以看出這種情況沒有切線.

生2:可是根據圖二的畫法,圖三的圖象左右兩側也該有兩條切線才對啊?(臺下有附和聲).

筆者一時也想不出更好的辦法來解釋,這個“意外”讓課堂陷入了沉寂,筆者隨即靈機一動,表示要與學生比比誰更快的找到解決方案,有想法的可以在明天為大家展示,學生的熱情一下被激發出來,個個躍躍欲試……

2 趁熱打鐵,揭示本質

第