在數學教學中怎樣培養小學生幾何直觀能力研究

石慶利

摘? 要：幾何直觀是數學的核心特性之一。在教育中充分利用幾何的直觀作用，并且借助幾何的直觀教育，在學生面前可以直觀地看到更復雜的數學問題，并且學生可以進行幾何直觀計算，并且分析和解決生活中的問題并幫助學生建立抽象思維，它與其他核心數學素質形成有機融合。幾何的直觀教學在數學的整個學習過程中扮演著重要的角色。

關鍵詞：幾何直觀;數學教學;培養

前言：小學數學學習是開啟學生數學學習生涯的關鍵。它激發了學生對數學的興趣，并鼓勵他們積極參與隨后的數學學習活動。幾何的直觀能力是學習數學的重要內容。它不僅可以幫助學生有效地學習數學知識和技能，還可以幫助他們改變解決實際問題的思路，提高解決問題的能力。

一、培養小學生幾何直觀能力的重要性

（一）幫助學生快速解題

小學生相對較小，因此他們的邏輯思維和空間想象力也受到限制。不能完全理解數學。通過訓練學生的幾何和直覺能力，學生在遇到問題時會不斷分析和簡化問題，建立圖形形式，并清楚地理解數學中隱藏的問題。了解解決問題的信息，研究的重點，并輕松解決數學問題。使學生在數學教室中的學習變得更加輕松和愉快，并使學習過程更加順暢。并且學生還將積極參與學習，逐步提高教育質量。

（二）可以幫助學生建立正確的數學知識體系

在數學中形成知識概念的過程是相對抽象和復雜的。空間形式和數量之間的關系也是一種思維形式，它反映了數學對象的基本屬性。老師的指導有助于學生對數學概念有更深入的了解，并建立正確的數學知識體系。數字和形狀是數學研究中最古老、最基礎的學科。他們可以在一定條件下實現轉化，并幫助學生學習。培養幾何直覺可以將數學知識與空間聯系起來，這不僅可以減少學生花在學習知識上的時間，還可以增強他們對數學知識的記憶。將數字和形狀組合在一起的學習過程逐漸滲透到數學知識的本質中。這不僅簡單快捷，而且還可以幫助學生發展思維，理解感知數學知識的本質，在實驗中找到數學知識的方法，實現數學思維的再次散發。

二、如何培養小學生的幾何直觀能力

（一）在數形結合中發展幾何直觀

華羅庚說：“數形結合百般好，數形隔離萬事休。”熟練地使用幾何直觀將復雜的計算問題轉換為簡單的計算問題，并訓練學生使用“圖形語言”來思考問題，也就是幾何直觀力。數軸在理解數字的意義上起著重要的作用。例如：使用數軸可以了解正數和負數的含義以及分數的含義。在借助幾何圖形教授相同分母分數的加減法計算時，學生意識到5個八分之一加上三個八分之一，是一個完整的圖形，這個結果為1。避免出現學生將1寫為八分之八的現象。比較分數大小，使用直觀的圖形比較分數大小，并讓學生總結如何比較相同的分母和相同的分子。又例如，當使用直觀的學習工具（包含100平方厘米的正方形網格圖卡）來教學面積單位的進率時，請學生觀察100平方厘米等于1平方分米。使用數字和形狀的組合進行組合，將抽象的數學知識在視覺上由幾何圖形直觀地表示出來。

（二）用模型和多媒體豐富幾何直觀

應該使用模型和多媒體演示來理解更復雜和難以理解的知識。沿其高度切割圓柱后，表面積和體積如何變化？如果將圓柱體切成多個部分，則表面積如何變化？這些問題是在模型的幫助下提出的，使學生能夠了解切割后增加圓柱體表面積的過程。在借助多媒體演示研究圓柱體與底部面積相等，高度相同和體積相同的圓錐體之間的關系時，相等底面積和高度相同的圓錐體的體積為圓柱體體積的三分之一，反之則為三倍。同樣，具有相同體積等底部面積的圓錐體的高度是圓柱體高度的三倍，反之則為三分之一。等高的圓錐體的底面積是圓柱體的三倍，反之則為三分之一。

（三）畫圖分析解決問題，合理利用幾何直觀

1.畫示意圖分析解答問題

（1）倍數問題

幫助學生在學習“倍數”問題時，需要讓學生理解“倍數”的兩種乘法和一種除法問題，可以通過一些圖形分析解決方案。

從示意圖中，可以直觀地看到多個數字之間的關系，并且通過畫圓和畫圖，可以進一步感受到“倍”的含義。

（2）歸一問題

例：媽媽買3個盆用了18元。如果買8個同樣的盆，需要多少錢？

繪制示意圖以分析歸一化問題，并幫助三年級學生突破乘法與除法之間不可理解的定量關系。通過為學生繪制直觀的圖表來學習理解抽象的定量關系，并改變過去使用無聊的乘法和除法的單一學習方法來理解數量關系。

2.畫線段圖分析解答問題

（1）畫線段分析，理解倍數問題之間的份數關系

從線段圖中，學生可以直觀地看到通過乘法計算的倍數，其中軍棋為一倍數，象棋是幾倍數，了解如何使用線段圖分析解決多個問題。

（2）畫線段分析，找列解方程解應用題的等量關系式

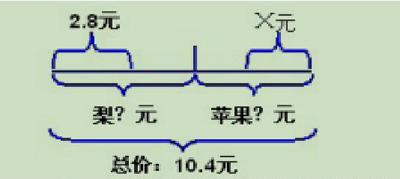
例如：李阿姨買了蘋果和梨各2千克，共花了10.4元，梨每千克2.8元，蘋果每千克多少元？

從線段圖中，可以一眼看出梨的單價與數量之間的關系，蘋果的單價與數量之間的關系以及兩種水果與總量之間的關系。通過畫一條線，可以清楚地找到定量關系之間的對應關系，并且學生可以了解列公式的原因。

可見，幾何直觀可以幫助學生直觀地理解數學，在整個數學學習過程中都發揮著重要作用。

結束語：

綜上所述，幾何圖形可以在生活中的任何地方找到，學生可以感受到生活的豐富性。通過教學和練習不同的案例，可以了解學生的幾何直覺的發展并提高他們解決問題的能力。總而言之，無論使用什么方法來發展幾何直觀，它都是一種全面發展學生幾何直觀的策略。引導學生學習更廣泛的平面幾何，并進一步發展他們對幾何圖形概念的理解。因此，在整個數學教育中應強調幾何直觀，并進行幾何直觀能力的訓練。

參考文獻：

[1]劉梅蘭. 小學生幾何直觀能力培養的實踐研究[D].南京師范大學，2019.

[2]魏鳳英. 小學數學中段生幾何直觀能力的培養策略研究[D].云南師范大學，2018.

[3]丁小紅. 小學生幾何直觀能力培養的教學設計研究[D].重慶師范大學，2018.

★ 本文系河南省教育科學規劃一般課題“小學數學幾何直觀的教育價值及策略研究”的研究性成果，課題批準號：2020YB1107