基于數學本質，設計學生學習路徑

曹燕

摘? 要：數學學習是數學知識的建構過程。在教學中，教師的教是為學生的學而服務的。教師應引導學生主動學習、深度學習。如何引導學生更好地學習，教師應從數學這門學科的本質出發(fā)，設計對學生學習有利的路徑，讓學生經歷數學學習的過程，使學生的學習具有高效率，思考更深入，知識應用更靈活。

關鍵詞：數學本質;學習路徑;數學思考;數學素養(yǎng)

《義務教育數學課程標準（2011年修訂版）》指出：教師要發(fā)揮主導作用，處理好講授與學生自主學習的關系，引導學生獨立思考、主動探索、合作交流，使學生理解和掌握基本的數學知識與技能、數學思想和方法，獲得基本的數學活動經驗。

數學學習是數學知識的建構過程。在教學中，教師的教是為學生的學而服務的。教師應引導學生主動學習、深度學習。如何引導學生更好地學習，教師應從數學這門學科的本質出發(fā)，設計對學生學習有利的路徑，讓學生經歷數學學習的過程，使學生的學習具有高效率，思考更深入，知識應用更靈活。

一、基于數學本質，以知識建構設計學習路徑

建構主義理論指出：學習是學習者基于原有的認知經驗生成意義，建構理解的過程。依據建構主義理論，教師應從學生已有的認知經驗出發(fā)，設計知識“建構化”的流程，創(chuàng)設最適合學生數學學習路徑。教師應充分了解學生的已有認知經驗，針對性地開展教學研究，讓學生的數學思考走向深度，促進學生的數學理解。

例如，教學蘇教版小學數學三年級下冊“含有小括號的兩步混合運算”時，教師就是通過先了解學生已有的兩步混合運算的認知基礎，設計有層次的教學活動，引導學生經歷知識的建構過程，讓學生的學習有“徑”可循。

（1）設計只含有同一級運算兩道復習題。

出示兩道習題，引導學生回憶同一級運算的運算順序。

出示：56-8+12，42÷6×4。

明確指出：56-8+12和42÷6×4都要按從左往右的順序進行計算。

（2）設計混合運算的兩道復習題。

出示兩道習題，引導學生回憶混合運算的運算順序。

出示：6+4×3，72-6×7。

教師引導學生通過具體的計算實例，進一步明確兩步混合運算中必須要遵循的基本運算順序，為含有小括號的兩步混合運算做好鋪墊。

（3）創(chuàng)設具體的情境，探究含有小括號的兩步混合運算。

出示：一個書包20元，一本筆記本5元，求購買一個書包后，還可以買幾本筆記本？

引導學生思考：要求還可以買幾本筆記本，先要求出什么？

學生嘗試列式解答：50-20÷5。

糾錯：這樣的式子有沒有問題？先求50元買一個書包后，還剩多少元？就是求50減20的差，前面列出的式子，是先算20除以5的商，思路不對，怎么辦？

引出：加括號改變運算順序，突出有括號的，先算括號里的運算。

在教學中，教師設計了括號作用的學習路徑，突出小括號的作用，引發(fā)認知上的沖突，讓學生體驗括號改變運算順序的重大作用，為學生建構知識提供了發(fā)展空間。

二、基于數學本質，以主動學習設計學習路徑

數學知識的學習，更多地需要學生積極主動地學習。學生積極主動的學習，依賴于學生對于學習內容的興趣，能不能投入精力，進行持久的學習。在學習的過程中，能否進行學習的自我調節(jié)、控制和反思。在數學教學中，教師應從培養(yǎng)學生的學習能力的角度出發(fā)，基于數學知識的本質，設計讓學生主動學習的學習路徑。

如蘇教版小學數學四年級下冊“平行四邊形的認識”教學中，教師就是從發(fā)展學生的主動學習的能力的角度出發(fā)，進行合理設計學習路徑，引導學生對平行四邊形的基本特征展開探究學習的。

在課前，教師已充分了解學生對平行四邊形的已有認知，進行相關復習，喚醒學生對于平行四邊形知識的回憶。在二年級時，學生已經認識了平行四邊形，能夠從直觀上識別一個圖形是不是平行四邊形，也能通過拼、剪、圍出平行四邊形，但對平行四邊形的基本特片并沒有清晰的認識。因此，教師就是從關注學生的經驗出發(fā)，從學生直觀的認識發(fā)展到抽象的思考。

（1）用4根小棒圍長方形，喚醒回憶。

師指出：研究一個平面圖形時，通常從邊和角的特征來研究。

（2）用4根小棒圍平行四邊形，主動學習。

師：剛才圍成長方形的4根小棒，還能圍成什么樣的圖形？（平行四邊形）

師：平行四邊形有哪些特征呢？我們可以從哪些方面展開研究？

讓學生在方格紙上畫平行四邊形，研究平行四邊形的特征。

師追問：那說明平行四邊形的上下的對邊是互相平行？左右的對邊也是互相平行？

量一量平行四邊形，4條邊的長度，你發(fā)現了什么？

……

從學生已有的生活經驗出發(fā)，引導學生從不同的角度豐富對平行四邊形的認知，注重啟發(fā)學生思考和進行簡單的推理，讓學生對平行四邊形的特征的認識由模糊走向清晰。

三、基于數學本質，以知識應用設計學習路徑

古語云“學以致用”，就是突出知識要應用于實際才有價值。在數學教學中，教師要突出以知識應用來設計學習路徑，給學生指明方向，利用數學知識的應用，實現數學問題的解決，鞏固學生的認知，強化數學知識的理解，形成數學技能。

如蘇教版小學數學三年級下冊“長方形和正方形的面積計算”的教學中，教師就是以知識應用為抓手，不斷豐富學生的認知經驗，引導學生建立應用的意識，讓學生親歷知識的發(fā)生、發(fā)展過程，感悟數學知識解決問題的步驟與方法。

（1）以熟悉的生活情境，應用知識，解決問題。

在推導出“長方形的面積=長×寬”之后，教師出示教室情境圖。

師：同學們，如何知道我們教室地面的面積是多少平方米呢？怎么辦？

（2）借助變化，類比中遷移知識，解決問題。

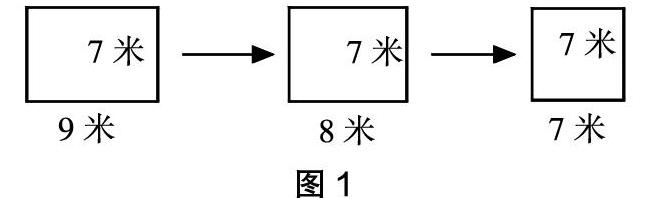
出示教室地面的長方形。

問題1：如果把長方形的長減少1米，長是多少米？長方形的面積怎樣求？

問題2：如果把長方形的長再減少1米，長是多少米？長方形的面積怎樣求？

……

師指出：長方形的長和寬變得一樣長，變成了一個正方形。

正方形的面積=邊長×邊長。

這里的教學設計中，教師不斷地讓學生感悟長方形的長變化，由長方形遷移到正方形，讓學生感知到長方形和正方形面積計算方法的聯系。既鞏固了新知的認識，又促進了學生的發(fā)展，進一步提高了學生的成功體驗。

四、基于數學本質，以知識脈絡設計學習路徑

數學知識的學習一般會經歷新課學習、單元復習和期末總復習三個階段。在新課學習時，教師主要以單獨的點狀知識進行教學，幫助學生理解和鞏固新的知識，構建認知結構。這類知識是松散型的點狀知識。在單元復習時，已經把一個單元中的松散型的點狀知識，各個知識點之間合并在一些進行學習，幫助學生結成知識小網絡。在期末總復習時，教師從整個知識的體系出發(fā)，分析知識之間的橫向聯系和縱向聯系，從學生的學情出發(fā)，設計易于學生展開學習的路徑，引導學生對所學習的知識進行有序整理、有條理復習，結成數學知識網絡，發(fā)展學生的數學學習能力。

如蘇教版小學數學六年級下冊“立體圖形的體積復習”時，教師就是依據學生的實際情況，設計了學習路徑。

（1）請自己整理出小學階段所學過的常見的立體圖形，畫出每個圖形的透視圖，并思考每個立體圖形的體積計算公式。

（2）回憶每個立體圖形的體積計算公式的推導過程，思考這些立體圖形體積之間的聯系。

（3）把有聯系的立體圖形擺放在一起。

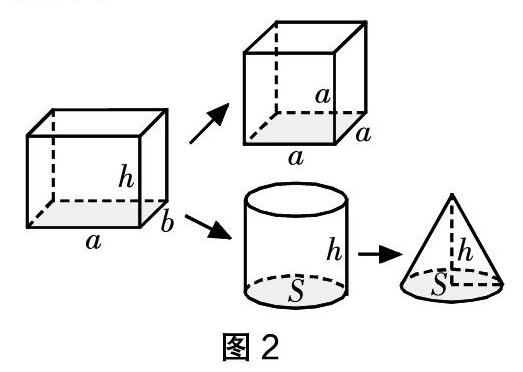
結合學生交流體積公式及其推導過程，呈現：

讓學生在立體圖形的下面填寫體積計算公式。

（4）學生交流常見立體圖形的體積計算公式推導過程，交流整理的方法。

（5）整理說明：從剛才的整理、交流中可以看出，首先得到的是長方體的體積計算公式，正方體是特殊的長方體，可以直接利用長方體的體積計算公式推導，圓柱轉化長方體得出體積計算公式，圓錐的體積是與它等底等高的圓柱體積的三分之一。長方體、正方體、圓柱的體積都可以用底面積乘高來計算。推導的過程，應用了圖形的特征的內在聯系和轉化的方法。

教師設計有步驟、可操作性的復習活動，展現了一個把零碎、松散的知識點建構成網絡的學習路徑：知識點——聯系——網絡。在數學學習中，獲取信息、優(yōu)化信息，也是學習的一個關鍵環(huán)節(jié)。在數學教學中，基于數學知識的本質，找出知識之間的聯系，幫助學生形成知識網絡，更利于學生清晰地理解數學知識，豐富學生的數學學習經驗，使學生的學習能力和思維品質不斷得以增長，為培育學生的數學核心素養(yǎng)創(chuàng)造更廣闊的空間。

五、結語

在數學課堂教學中，教師要有意識地設計學生的學習路徑，引導學生自主建構知識，把零散的知識點溝通聯系、串聯起來，使知識形成網絡，幫助學生更好地掌握數學知識，提高學習數學和解決問題的能力。