基于整體視角的教材解讀與教學設計

顏廷亮

[摘? 要] 學生學習知識應該是一個連續建構的過程，每一個學段的教學都應該從整體中來，到整體中去. 教師要基于整體視角對教材進行解讀，理清知識之間的縱橫聯系，挖掘知識所承載的育人元素. 基于整體視角，相互聯系、逐步深入的問題串能幫助學生有效建構知識體系，能使教學行為從學習知識技能、積累活動經驗的層面，過渡到核心素養整體發展的層面.

[關鍵詞] 整體視角;教材解讀;核心素養;教學設計

現行《義務教育數學課程標準（2011年版）》為了體現數學課程的連續性和整體性，統籌考慮九年的課程內容，根據學生身心發展和認知特點，將九年的數學學習時間分為1～3年級、4～6年級、7～9年級三個學段，這就會給師生帶來不少內容“曾經學過”的錯覺，認為過于“簡單”，從而“輕視”. 事實上，教材的編寫一般是按照知識體系螺旋上升的，即使“再次出現”，其教學目標也絕對不是當初出現的要求，這就要求教師從整體的視角來解讀教材、把握目標要求. 如“平面圖形的認識（一）”中談到線段、射線、直線、角等概念，不少教師認為小學里已經學過，學生“不教也會”，可見教師對“會”的理解還停留在認知表面. 之所以造成這樣的認識封閉，主要是因為教師對教材的整體解讀不夠到位，長此以往，非常不利于學生數學學科核心素養的培養. 下面以蘇科版七下“第6章？搖平面圖形的認識（一）”中的“6.2 角（1）”為例，從整體性視角方面談談筆者對這節課的教材解讀與教學設計.

基于整體視角的教材解讀

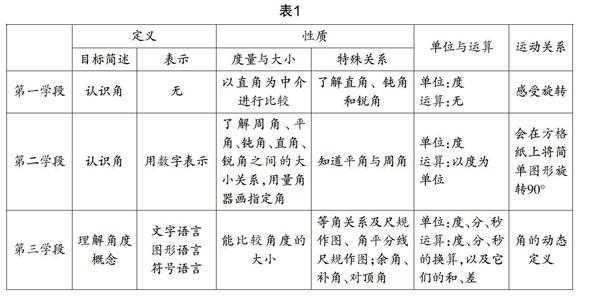
課程標準三個學段中，關于角的知識羅列如表1.

從表1的縱向比較中可以看出，角的定義從認識到理解，從靜態到動態，從圖形語言到三種語言的表征，要求越來越高，為后續高中學習任意角的概念做了鋪墊，是螺旋上升且統一、連續的，這樣，對于角這個知識點，我們就找到了它的生長點、發展點與延伸點;學生經歷了最初的觀察、體驗，到最終的歸納、提煉，思維要求是越來越高的;角度的度量與大小比較從最初的以直角為中介進行比較，到后來的度量與疊合法比較，方法要求、操作要求越來越高，對特殊關系的研究也從了解、知道轉向更多的特殊關系研究，進而提出尺規作圖的要求，這樣的過程既符合學生的身心發展和認知特點，又體現了數學“從定性到定量”的研究方式，對學生思維能力的要求在不斷提高.

從表1的橫向比較中可以看出，對角的研究路徑是逐漸清晰的，從第一、第二學段的不明確，到第三學段的“引入—定義—性質—聯系—運用”，知識關聯線逐漸形成，顯化了研究套路，強調“情境—知識—運用”，讓學生多次經歷與感悟“抽象—演繹—建模”的過程，逐步加深學生對基本數學思想方法的認識.

從顯性的知識層面來看，點、線（角）、面的認識是平面幾何的初步認識，是最基本的圖形，在此基礎上建立“圖形與幾何”這個板塊的大廈，而角在其中的地位可謂承上啟下：由“點到點”的研究產生線（線段、射線、直線的定義與表示，中點、尺規畫等長線段、兩個基本事實），它可以為學習角的知識（線與線的關系）提供類比與對比的素材，提供研究路徑，通過系列學習活動，學生可以獲得對比、類比及顯化研究套路等基本活動經驗，經歷“抽象、演繹、類比、對比、轉化、建模”等過程，培養學生基本的數學思想方法;后續相對“復雜”的幾何圖形，都可以“拆分”為基本的幾何元素（點、線、角）來研究元素之間的關系（獲得性質），或者經歷從復雜到簡單的思維轉化，也可以用基本的幾何元素組合出有價值的幾何圖形來研究（獲得研究對象），把握圖形之間的轉化關系，這些都是“圖形與幾何”學習的基礎. 從上面幾點解讀可以看出，對知識層面的認識實際上就包含了隱性能力培養的可能.

上述從整體視角對“角”的教材進行解讀，不僅可以幫助學生為構建知識體系做準備，而且能夠為教師全面理解數學并有效進行設計提供幫助，這樣的整體性深度解讀實際上就決定了我們課堂的高度，為課堂教學中培養學生的數學抽象、數學建模、直觀想象等數學學科核心素養提供了路徑.

基于教材解讀的教學設計

1. 環節一：生活數學

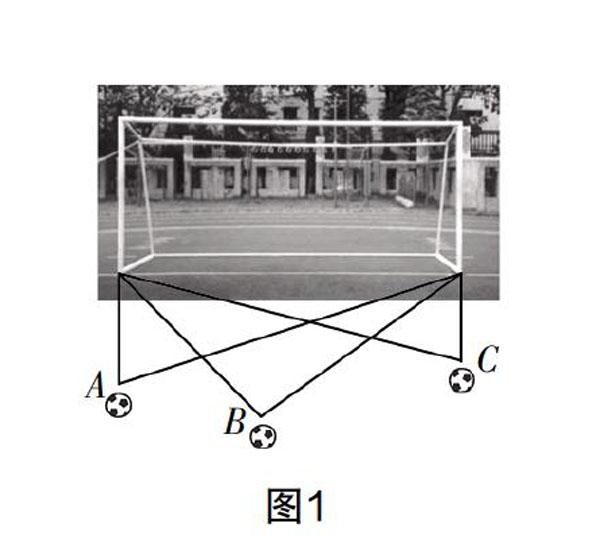
問題1：在足球場上，球員在什么位置射門（如圖1），進球的可能性越大？為什么？大小如何測量？

設計意圖 數學來源于生活，要讓學生從實際生活情境中抽象出數學問題，學會用數學的眼光看世界. 生活情境問題化，明確估測角度大小、測量角度的方法，得到研究的對象——角.

2. 環節二：知識關聯

問題2：前面一小節我們學習了線段，研究的是點與點之間的關系（兩點距離、線段、兩點確定一條直線），那么角研究的是哪些元素之間的關系？（線與線）

問題3：小學里我們就知道了角，那么你能說說什么叫角嗎？怎么定義？如何表示？

問題4：前面一小節我們學習了線段、射線與直線，請你說說我們學習了線段的哪些內容，采用的研究方法是什么，并猜想關于角的研究內容是什么.

在教師的幫助下，在與學生的對話中，師生共同逐步完成圖2.

設計意圖 通過問題串引領，幫助學生尋找知識的生長點與發展點，知道線段是描述位置差異的，而角是描述方向差異的. 體會兩者異同，通過類比與對比，幫助學生強化研究路徑，從數學知識的內部結構去獲得新的研究對象與新對象的研究方法;培養學生的問題意識，學會發現問題并提出一些本源性的問題，為分析問題和解決問題打好基礎，讓學生學會用數學的思維去思考世界.

問題5：圖3與圖4如何表示？有幾種表示方法？圖3與圖4如何比較大小？圖5中共有多少個角？請分別表示這些角. 你能說出一些大小關系與和差關系嗎？

設計意圖 這是本節課的核心——鞏固角的符號表示，同時讓學生初步從“形”的角度，直觀地感受角的大小、和差關系，為下一個環節的學習做好鋪墊. 教師應該重視三種數學語言表征的轉化，讓學生學會用數學的語言去表達，并通過拆分與組合體會圖形的轉化.

3. 環節三：思想方法

問題6：從“問題5”可以看出，從“形”上，角可以比較大小以及和差運算，那么從“數”上，角又該如何比較大小，如何進行和差運算呢？請舉例說明.

設計意圖 數學是研究數量關系與空間形式的科學，教學中要反復讓學生感悟從幾何圖形的定性到定量的研究，讓他們逐步掌握數形結合思想方法.

問題7：類比線段的大小比較與和差計算的單位，即米、分米、厘米等，角度有沒有更小的單位呢？它們之間的換算關系是什么？可以通過類比時鐘的時間表示方法來進行思考.

設計意圖 認識度、分、秒及換算. 在“問題6”中，學生舉的例子會受限于單位，教師可以引導學生提出“問題7”.

4. 環節四：矛盾轉化

問題8：（課堂小結）（1）本節課你學到了哪些知識點？這些知識點從何而來？下節課還會研究什么？

（2）本節課除了知識點，你還學到了什么？請與大家分享.

（3）本節課學完后你還有什么疑惑嗎？

設計意圖 引導學生描述知識的源點與遠點，總結基本知識技能及思想方法，積累基本的活動經驗，體會“從一般到特殊”（研究一般角—研究特殊角）“從運動到靜止”（兩種定義、平角與周角的形成、大小比較）的研究過程，學會用數形結合思想去研究問題.

最后，送給同學們一幅圖（如圖6），我們不做井底之蛙，爭取最大視野，仰望星空，別忘了腳踏實地，這是做人做事的態度.

教后反思

1. 知識的整體性：呼喚教師“高屋建瓴”

從本課知識的視角看，角的知識是一個非常簡單的內容，但是知識與知識之間從來都是互動聯系、交織發展的，“知識點”要為“知識線”服務，甚至要為“知識面”服務. 這就要求我們不能停留在知識的淺表層次，也不能停留在本課知識的技能上，我們要樹立整體觀念，從整體性視角來提高解讀教材的能力. 只有這樣，才能讓原本“簡單”的知識不簡單，讓原來單薄的課堂豐厚起來;只有這樣，才能真正有效地落實學生的數學學科核心素養目標. 可以說，教師的高度決定了學生的視野.

2. 教學的整體性：需要教學“到位而不越位”

課堂不能停留在鞏固、重復小學已學的內容上，否則不利于學生的認知發展，也會讓學生越學越“迷茫”：學了還要學. 也不能過度深挖，甚至超前教學，讓學生用高中知識解決初中問題，這種只關注結果、揠苗助長的行為不利于學生思維的成長，長此以往甚至會讓學生對數學失去興趣. 數學的整體性要求教師基于整體視角，對所在的學段知識與方法進行整合，探索落實學生核心素養的路徑，教到位而不越位.

3. 學習的整體性：引導學生深度學習

學生學習數學的過程應該是“在森林中穿行”的過程，即清楚地知道自己所處的“森林”這一整體，又能探索出前行的“地圖”，更能欣賞沿途的“樹木”. 教師既要讓學生體會到研究幾何圖形或代數問題的一般套路，也要在學習相關知識點的時候及時關注、及時引導，讓學生適時停留思考、時常總結回顧，以思維圖等方式構建自己的知識整體. 教師要教會學生進行深度學習，因為這樣更加有利于核心素養這一整體課程目標的實現.