基于陶行知思想的高中數(shù)學(xué)教學(xué)情境創(chuàng)設(shè)探析

蔣浩強(qiáng)

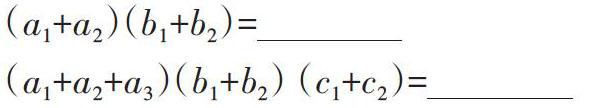
[摘? ?要]文章主要闡述基于陶行知思想，在高中數(shù)學(xué)教學(xué)中情境創(chuàng)設(shè)的探究，針對(duì)陶行知教育思想中的“生活即教育”“教是為了不教”“教學(xué)做合一”等相關(guān)理念做了簡要的闡述，并對(duì)其思想如何應(yīng)用于高中數(shù)學(xué)教學(xué)實(shí)踐中作了簡要的論述，以此體現(xiàn)陶行知先生教育思想的重要性和藝術(shù)性。

[關(guān)鍵詞] 創(chuàng)設(shè)情境;生活即教育;教是為了不教;教學(xué)做合一

[中圖分類號(hào)]? ?G633.6? ? ? ? [文獻(xiàn)標(biāo)識(shí)碼]? ?A? ? ? ? [文章編號(hào)]? ?1674-6058（2020）15-0054-02

數(shù)學(xué)新課標(biāo)指出，基于數(shù)學(xué)學(xué)科核心素養(yǎng)的教學(xué)活動(dòng)應(yīng)該把握數(shù)學(xué)的本質(zhì)，創(chuàng)設(shè)合適的教學(xué)情境、提出恰當(dāng)?shù)臄?shù)學(xué)問題，引發(fā)學(xué)生思考與交流，形成和發(fā)展數(shù)學(xué)學(xué)科核心素養(yǎng)，由此可見高中數(shù)學(xué)教學(xué)中情境創(chuàng)設(shè)的重要性。由于高中數(shù)學(xué)比較抽象，所以情境創(chuàng)設(shè)其實(shí)就是把學(xué)生難以理解的知識(shí)的“學(xué)術(shù)形態(tài)”轉(zhuǎn)化為學(xué)生易于接受的“教育形態(tài)”，學(xué)生對(duì)數(shù)學(xué)的思考主要來自具體的情境。從學(xué)生平時(shí)熟悉的實(shí)際生活情境出發(fā)，提出相應(yīng)的問題，引導(dǎo)和啟發(fā)學(xué)生積極地思考、主動(dòng)地討論和探究，從而學(xué)習(xí)相關(guān)的數(shù)學(xué)思想方法，獲得在實(shí)際中如何應(yīng)用知識(shí)的體驗(yàn)。

近代著名教育家陶行知從中國國情出發(fā)，提出“生活即教育”“社會(huì)即學(xué)校”“教學(xué)做合一”等三大理論主張。2017版數(shù)學(xué)課程標(biāo)準(zhǔn)也指出，學(xué)生需要用數(shù)學(xué)的眼光在生活當(dāng)中捕捉數(shù)學(xué)問題，主動(dòng)并靈活地運(yùn)用數(shù)學(xué)知識(shí)思考和分析生活現(xiàn)象，自主地解決實(shí)際問題。所以，在數(shù)學(xué)教學(xué)中，教師應(yīng)多重視學(xué)生的生活體驗(yàn)，把數(shù)學(xué)中復(fù)雜的知識(shí)與學(xué)生的實(shí)際生活聯(lián)系起來，把數(shù)學(xué)中抽象的問題與生活中的實(shí)際情境結(jié)合起來，實(shí)施讓數(shù)學(xué)生活化、讓生活數(shù)學(xué)化的課堂教學(xué)。陶行知先生還積極倡導(dǎo)“教是為了不教”的教學(xué)理念，指出教師在教學(xué)時(shí)應(yīng)把握好核心的教學(xué)要義：授人以魚不如授人以漁。本文主要運(yùn)用部分陶行知教育思想，結(jié)合在高中數(shù)學(xué)課堂教學(xué)中的情境創(chuàng)設(shè)這一環(huán)節(jié)的應(yīng)用，進(jìn)行簡明的論述。

一、構(gòu)建實(shí)際生活情境，讓學(xué)生學(xué)習(xí)興趣得以激發(fā)

陶行知先生教育思想的核心就是“生活教育”，所以教師應(yīng)當(dāng)多借助學(xué)生平時(shí)生活中的實(shí)際體驗(yàn)來創(chuàng)設(shè)教學(xué)情境。這種生活化的教學(xué)情境，可以使得原本枯燥乏味、抽象難懂的數(shù)學(xué)知識(shí)更直觀，讓學(xué)生感受學(xué)習(xí)數(shù)學(xué)的樂趣、體會(huì)數(shù)學(xué)知識(shí)的價(jià)值，從而激發(fā)學(xué)習(xí)數(shù)學(xué)的興趣和學(xué)習(xí)的積極性，培養(yǎng)正確的數(shù)學(xué)意識(shí)。

[例1]在學(xué)習(xí)“算法語句”時(shí)，需要交換兩個(gè)變量a和b的值，如果教師直接給出程序框圖，學(xué)生可能會(huì)不易理解，教師可以結(jié)合實(shí)際生活中的常見例子，直觀地創(chuàng)設(shè)情境引入。如，若現(xiàn)在講臺(tái)上有兩個(gè)大的杯子A和B，A杯中盛滿了水，B杯中盛滿了牛奶，如果想將A中的水和B中的牛奶交換位置，應(yīng)該如何交換呢？教師可以繼續(xù)發(fā)問：“可不可以直接將水倒入牛奶中或直接將牛奶倒入水中？”學(xué)生立即回答：“不能，這樣的話水和牛奶就會(huì)混合到一起了。”“那怎么樣處理才能讓水和牛奶既不混合，又能交換位置呢？”教師追問。學(xué)生會(huì)答：“再拿一個(gè)空杯子C過來，將水倒入C中，將牛奶倒入A中，最后再將C中的水倒入B中即可。”

教師在此可以總結(jié)：同學(xué)們認(rèn)為要完成交換則需要借助空杯子。緊接著教師可以啟發(fā)學(xué)生引出問題：可否編寫一個(gè)程序框圖，交換兩個(gè)變量a和b的值？能不能直接將a和b直接交換呢？就如同剛剛我們所說的如何交換A杯中的水和B杯中的牛奶問題一樣，需要借助于空杯子C才能完成交換，那么按照這個(gè)思路，對(duì)于變量a和b的交換，則需要借助于一個(gè)新的變量c才能完成。此案例將抽象的數(shù)學(xué)問題轉(zhuǎn)化成學(xué)生生活中的實(shí)際問題，通過生活中實(shí)際問題的解決，從而學(xué)習(xí)數(shù)學(xué)問題的解決。

二、創(chuàng)設(shè)探究型的問題教學(xué)情境，讓學(xué)生主動(dòng)“學(xué)”

陶行知先生曾多次強(qiáng)調(diào)：“好的先生不是教書，不是教學(xué)生，乃是教學(xué)生學(xué)。”這正體現(xiàn)了陶行知思想中“教是為了不教”的理念。新課程標(biāo)準(zhǔn)也明確指出，讓學(xué)生在自主探究與合作交流中自主構(gòu)建知識(shí)。高中數(shù)學(xué)本身就具有較強(qiáng)的抽象性、邏輯性，要想讓學(xué)生更好地掌握所學(xué)知識(shí)，教師需要科學(xué)地構(gòu)建出可以讓學(xué)生自主探究的問題教學(xué)情境，促使學(xué)發(fā)現(xiàn)問題、探索問題、解決問題，在整個(gè)教學(xué)過程中讓學(xué)生主動(dòng)“學(xué)”。

[例2]二項(xiàng)式定理對(duì)學(xué)生來說是一個(gè)全新的內(nèi)容，教師教學(xué)時(shí)可以構(gòu)建如下的問題教學(xué)情境。

問題1：以上兩個(gè)式子展開后有幾項(xiàng)？每一項(xiàng)是怎樣構(gòu)成的？

[設(shè)計(jì)意圖]幫助學(xué)生回顧多項(xiàng)式乘法的法則，并引導(dǎo)學(xué)生歸納其中的規(guī)律：如何快速判斷展開式的項(xiàng)數(shù)？每一項(xiàng)是怎樣構(gòu)成的？（為后面探究二項(xiàng)式定理做鋪墊。）

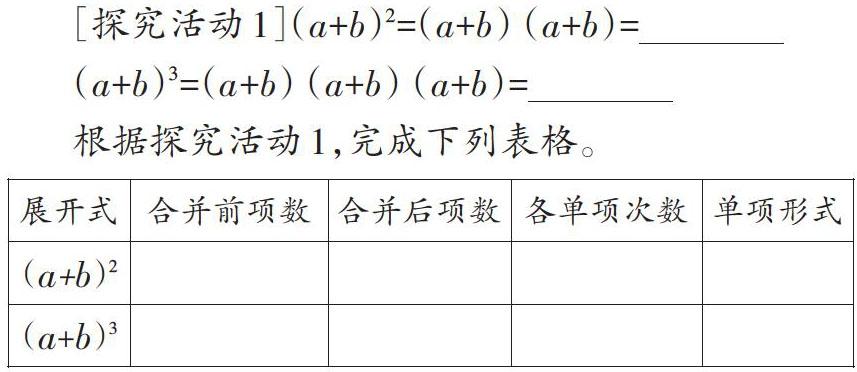
[探究活動(dòng)1]（a+b）2=（a+b） （a+b）=

（a+b）3=（a+b） （a+b） （a+b）=

根據(jù)探究活動(dòng)1，完成下列表格。

問題2：（a+b）2展開式未合并同類項(xiàng)前為什么是4項(xiàng)？

問題3：（a+b）2展開式中ab項(xiàng)的系數(shù)為什么是2？

問題4：（a+b）3展開式中ab2項(xiàng)的系數(shù)為什么是3？

問題5：口袋中有大小形狀相同的a、b兩個(gè)球，從中摸出1個(gè)球后放回，如果有重復(fù)的摸3次，摸到1次a球，2次b球會(huì)有多少種情況？

[設(shè)計(jì)意圖]通過以上表格數(shù)據(jù)及4個(gè)連續(xù)的問題，結(jié)合老師的引導(dǎo)，啟發(fā)學(xué)生從展開式中的“項(xiàng)數(shù)、次數(shù)、項(xiàng)的構(gòu)成及其系數(shù)”等方面來探究展開式的規(guī)律，其中的難點(diǎn)在于分析每一項(xiàng)的構(gòu)成并得到對(duì)應(yīng)項(xiàng)的系數(shù)。問題5的設(shè)計(jì)正是幫助學(xué)生將多項(xiàng)式乘法與計(jì)數(shù)原理建立聯(lián)系，從而理解ab2的系數(shù)為什么是c。（為后面推廣到一般情形，探索（a+b）n展開式中各項(xiàng)的系數(shù)做準(zhǔn)備。）

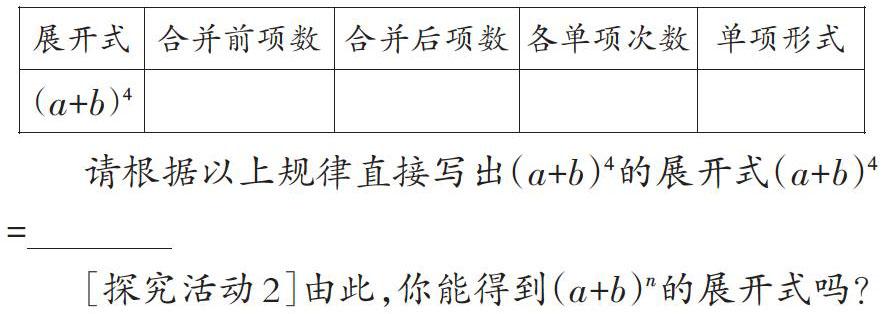
問題6：你能根據(jù)以上結(jié)論直接填寫下面的表格嗎？

請(qǐng)根據(jù)以上規(guī)律直接寫出（a+b）4的展開式（a+b）4=

[探究活動(dòng)2]由此，你能得到（a+b）n的展開式嗎？

[設(shè)計(jì)意圖]讓學(xué)生經(jīng)歷由特殊到一般的歸納總結(jié)，期間離不開對(duì)具體的特殊實(shí)例的分析。整個(gè)過程可以采用讓學(xué)生獨(dú)立思考或小組討論等形式，讓學(xué)生總結(jié)出二項(xiàng)式定理的表達(dá)式。

以上通過一系列問題串的設(shè)計(jì)，引導(dǎo)學(xué)生對(duì)一些典型和具體的實(shí)例進(jìn)行觀察、比較、分析、歸納，從中找出事物的本質(zhì)屬性，主動(dòng)構(gòu)建二項(xiàng)式定理的內(nèi)容，不僅體現(xiàn)了學(xué)生學(xué)習(xí)的主體性，培養(yǎng)了主動(dòng)學(xué)習(xí)的能力，而且提升了學(xué)生的數(shù)學(xué)運(yùn)算、數(shù)學(xué)抽象、數(shù)學(xué)建模等數(shù)學(xué)核心素養(yǎng)。

三、創(chuàng)設(shè)探究活動(dòng)型教學(xué)情境，讓學(xué)生在“做”中學(xué)

“教學(xué)做合一”是陶行知先生提出的一個(gè)重要理論。先生特別強(qiáng)調(diào)要在“做”中獲取知識(shí)。他說：“事怎樣做便怎樣學(xué)，怎樣學(xué)便怎樣教。教而不做，不能算是教; 學(xué)而不做，不能算是學(xué)。教與學(xué)都以做為中心，‘做是學(xué)的中心，也是‘教的中心。” 這些話特別強(qiáng)調(diào)實(shí)踐是認(rèn)識(shí)的先導(dǎo)，只有“做”了，“學(xué)”才能有收獲。另外，學(xué)習(xí)要在情境中去體驗(yàn);這也正是新課程倡導(dǎo)的： 學(xué)生要樂于探究、勤于動(dòng)手，培養(yǎng)主動(dòng)探究、自主學(xué)習(xí)的能力。

[例3]為了幫助學(xué)生更好地理解與掌握橢圓離心率的定義，教師可事先準(zhǔn)備如下用具： 一塊紙板，兩個(gè)圖釘，一根長約20cm的細(xì)繩。

[探究活動(dòng)1]用圖釘將橢圓的焦點(diǎn)固定（即將橢圓的焦距2c固定），然后將細(xì)繩的兩端固定在焦點(diǎn)處，用鉛筆筆尖拉緊細(xì)繩，在紙板上畫一個(gè)橢圓，接著再改變繩子的長度（即改變2a的大小），繼續(xù)畫橢圓，觀察這些橢圓“扁”的程度變化情況。

[探究活動(dòng)2]固定細(xì)繩的長度（即2a不變），調(diào)整圖釘之間的距離（即改變2c的大小），畫幾個(gè)橢圓，觀察這些橢圓“扁”的程度變化情況。

問題：大家在動(dòng)手畫橢圓的過程中，發(fā)現(xiàn)有什么規(guī)律嗎？

通過親自實(shí)踐，結(jié)合學(xué)生間的相互討論，教師再以適當(dāng)?shù)膯栴}做引導(dǎo)，學(xué)生就很自然地得出刻畫橢圓形狀“扁”的程度的量離心率 e=[ca]。

以上的教學(xué)過程是以學(xué)生親自畫圖為教學(xué)情境，通過觀察改變a、c兩個(gè)量后，橢圓形狀發(fā)生的變化，從中發(fā)現(xiàn)橢圓的離心率與橢圓形狀的關(guān)系。整個(gè)過程以學(xué)生自主探究為主，很好地體現(xiàn)了“教學(xué)做合一”的教學(xué)理念。

總之，在高中數(shù)學(xué)課堂教學(xué)實(shí)踐中，特別是情境創(chuàng)設(shè)這個(gè)教學(xué)環(huán)節(jié)上，筆者已經(jīng)深刻地感受到陶行知先生教育思想的重要性和藝術(shù)性。在數(shù)學(xué)教學(xué)課堂上，教師不僅要讓學(xué)生學(xué)習(xí)數(shù)學(xué)知識(shí)，更重要的是培養(yǎng)學(xué)生的數(shù)學(xué)思想和用數(shù)學(xué)思維方法去發(fā)現(xiàn)問題、思考問題、解決問題的能力。要做到以上這點(diǎn)，也要求教師及時(shí)將教育理念和課堂教學(xué)相結(jié)合，這樣才能使學(xué)生得到知識(shí)素養(yǎng)和學(xué)習(xí)技能的“雙豐收”。

[? ?參? ?考? ?文? ?獻(xiàn)? ?]

[1]? 中華人民共和國教育部. 普通高中數(shù)學(xué)課程標(biāo)準(zhǔn)（2017版）[M].北京：人民教育出版社，2017.

[2]? 張奠宙，王振輝.? 關(guān)于數(shù)學(xué)的學(xué)術(shù)形態(tài)和教育形態(tài)——談“火熱的思考”與“冰冷的美麗” [J]. 數(shù)學(xué)教育學(xué)報(bào)，2002（2）：1-4.

（責(zé)任編輯? ? 黃諾依）