非“圖形與幾何”領域中開出的“幾何之花”

強震球 中學高級教師，江蘇省優秀青年教師，江陰市首批名教師，市兼職教研員。先后獲得江陰市、無錫市和江蘇省小學數學課堂教學優質課評比一等獎，全國第八屆深化小學數學教學改革觀摩交流會一等獎第一名。應邀在全國二十多個省（市）、自治區的教學觀摩活動中執教觀摩課或講座，深受一線教師好評。

主持多個課題研究，省級課題“小學三年級學習成績分化的成因及對策研究”獲得江蘇省精品課題，江蘇省教學成果特等獎。

【摘要】“幾何直觀”主要是指利用圖形描述和分析問題，具體來說就是依托、利用圖形進行數學的思考和想象。它在本質上是一種通過圖形所展開的想象能力，也是一種思維活動。本文強調在“數與代數”及其他非“圖形與幾何”領域的教學中，研究如何用幾何直觀的方法培養學生的幾何直觀表征問題的意識和能力，以及表征之后的頓悟與反思能力，找到解決問題的思路，彰顯幾何直觀的價值，促使學生認識幾何直觀在數學學習過程中的重要作用，初步學會用幾何直觀的方法思考和學習數學，真正讓“幾何之花”開遍學生數學學習的全過程。

【關鍵詞】幾何直觀 模型 數學素養

一、花開“數軸模型”，變抽象為形象

數學上，數軸是個一維的圖，它是一條規定了原點、方向和單位長度的直線。所有有理數都可以用數軸上的點來表示，也可以用數軸來比較兩個有理數的大小。數軸是運用幾何直觀的最佳模型之一，靈活應用數軸，能起到化繁為簡、事半功倍的效果。實踐中，我們發現數軸能夠幫助學生更直觀、更深入地認識數，更準確地理解數與數之間的關系，為學生數感的建立起到積極作用。

例如五年級“認識負數”一課中，借助數軸，學生就能很好地從本質上理解正負數的意義，以及“0”的作用。在教學中，教師可以由一個不完整的溫度計（沒有0的溫度計），逐漸轉變成半直觀半抽象的數軸，最后形成完整的數軸模型。利用數軸可以開闊解題思路，解決諸如表示點的位置、進行數的大小比較等問題，表示正數的點在原點的右邊，表示的數越大，這個點到原點的距離也就越遠;表示負數的點在原點的左邊，這個點到原點的距離越遠，則這個負數就越小;0在數軸上是用原點來表示的。在認識負數以前，學生常常認為“0”是最小的數，或者表示“沒有”，現在再通過數軸來看數字“0”，學生就能重新認識它的地位和意義了。

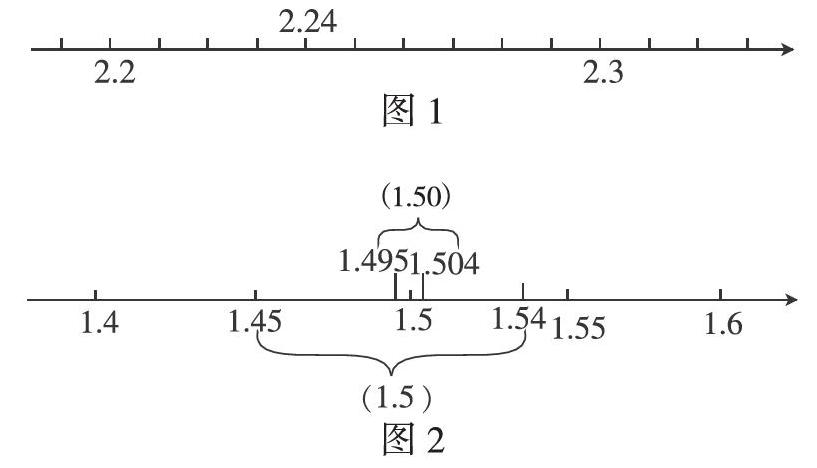
再如，在教學“近似數”的內容時，學生利用數軸就可以直觀、形象地理解一個小數的近似數的原理以及精確度的概念。如：“2.24更接近哪一個一位小數？為什么？”有一定數感的學生可能會馬上知道結果是2.2，但是能真正理解“為什么是2.2？”的同學并不是很多。于是，教師在這時就請出數軸來幫助學生直觀地理解其中的道理。如圖1，

經過數軸的幫助，學生能很直觀地看出2.24更接近2.2，所以它的近似數是2.2。又如“1.5和1.50都是1.496的近似數，哪一個更精確？為什么？”這個問題是比較有挑戰性的，借助數軸來幫助學生理解這個問題就顯而易見了。如圖2，

從數軸上可以清楚地看到1.5的范圍是1.45～1.54，1.50的范圍是1.495～1.504。近似數為1.50的范圍比大約1.5的范圍小，由此可見，1.50更精確，精確度也更高。

二、花開“算式模型”，變復雜為簡單

在數學中，算式是指在進行數（或代數式）的計算時所列出的式子，包括數（或代替數的字母）和運算符號（四則運算、乘方、開方、階乘、排列組合等）兩部分。按照計算方法的不同，算式一般分為橫式和豎式兩種。每一種算式都有著自己固定的模型，而算式中的每一部分彼此間又有著看似簡單卻密不可分的聯系。借助算式模型，以及算式中各部分之間的關系，能有效地幫助學生解決“數與代數”領域中出現的拓展性問題。

例如，學生在四年級學習了“兩位數乘三位數的乘法”后，會有這樣的思考：“用1、2、3、4、5這五個數字組成一個兩位數和三位數，要使積最大，應是哪兩個數？要使積最小呢？”對于一般的學生來說，這個問題的難度很大，還有一部分學生會用口訣“差大積小，差小積大”來解決，但是這句口訣學生真正理解嗎？教學中筆者努力嘗試用直觀的方式來幫助學生解決這個問題。經過嘗試和研究，發現利用豎式模型（圖3）能便于學生順利地找到結果。

我們知道，在計算三位數乘兩位數的時候，最高位上相乘就能初步確定積的大小。求積的最大值時，首先考慮①、②號位置上的數字相乘的結果要最大，就要選數字4、5，而數字5一定要放在①號位置，因為用5乘三位數的十位和個位，所得的結果比用4乘三位數的十位和個位所得的結果大。接著，考慮④號位置上只能是數字3，因為3乘兩位數的結果大。其次，③、⑤位置上放1、2，而數字2一定要放在③號位置上，因為2乘三位數比1乘三位數的結果大。由此，我們也不難發現，將1～5這五個數，按從大到小的順序，依次填寫在①—⑤號位置上（如圖3箭頭所指），所以結果是431×52的積最大。而求積最小的情況，則與最大值的情況相反，所以結果是245×13的積最小。

再如，五年級有這樣一個挑戰題：“小馬虎計算30.6除以一個數時，由于把除數的小數點向左點錯了一位，結果得到12。原來的除數是什么？”解題時很欣喜地看到學生能自主運用直觀模型來解決，利用除法算式模型、除法各部分之間的關系以及對與錯兩次的對比變化，學生呈現了變化的過程，將文字直觀化，進而對照直觀模型利用倒推等策略順利地解決這個問題。

三、花開“線段圖模型”，變混淆為清晰

線段圖是由幾條線段組合在一起，用來表示應用題中的數量關系，幫助學生分析題意、解決問題的一種平面圖形。它是從抽象的文字到直觀的再創造、再演示的過程。線段圖，以其形象、直觀的特點，在數學教學中廣泛應用。在數學教學中，注重讓學生運用線段圖這個模型來解決實際問題，能有效地提高學生的自主學習能力，使學生學會學習。例如，在教學四年級“一一間隔規律的實際問題”時，教師出示例題：“一條林蔭道上共栽了7棵樹，相鄰的兩棵樹相隔3米。林蔭道長多少米？”大部分學生看到題目后是茫然的，于是教師著重啟發學生思考7棵樹是怎么種的。當學生說出某種方法后，引導學生在草稿紙上畫出樹是怎么種的，討論得出：用點代表樹，用線段代表間隔3米。畫出第一個線段圖，如圖4， 教師隨后重點引導學生觀察線段圖，認清“什么和什么一一間隔排列”“頭尾是怎樣的情況”，并進一步引發思考“7棵樹一定只能這樣種嗎？”。有了第一個線段圖這個初步模型，學生便比較順利地思考出另外兩種情況的線段圖，一種是“頭尾都不種”，一種是“頭種尾不種”或者“頭不種尾種”（如圖5）。

就這樣，三種不同情況的線段圖模型就形成了。學生在畫圖、識圖、比圖的過程中，逐步強化植樹問題中的三種直觀模型，為后面解決求林蔭道長度的問題奠定基礎。之后呈現的兔子排隊問題，筆者就放手讓學生嘗試模仿，直接畫出直觀圖并解答。

四、花開“連線圖模型”，變內隱為外顯

在小學第一學段數學學習中，連線是學習中常用的一種數學方法，它的價值就在于能有序、不重復、不遺漏地進行數學分析，將隱藏在頭腦中的思維過程外顯，從而最終找到所求問題的結果。在第二學段的教學中，教師要好好利用連線圖的數學價值，將比較復雜的思維過程直觀地呈現在連線圖中，以便學生更有利地繼續展開數學思考，找尋數學規律，解決數學問題。

例如，在教學“搭配的規律”中，為了讓學生找到蘊藏在搭配中的規律，教師可以引導學生進行連線，將搭配的過程清晰地表示出來。學生呈現的可以是完整的連線圖（如圖6），繼而教師逐步引導學生過渡到半抽象的連線圖（如圖7）。

但是不管是哪一種連線圖，都要讓學生借助連線圖明確：每一頂帽子都可以和4個不同的木偶搭配，那么有4種不同的搭配方法。有3頂不同的帽子，那么就有3個4種，也就是3×4=12種不同的搭配方法，進而得出搭配的規律——兩種不同類的物體搭配所得的搭配方法數=兩種物體的數量相乘。

幾何直觀是揭示現代數學本質的有力工具，有助于學生形成科學正確的世界觀和方法論，而直觀模型在培養幾何直觀的過程中起著重要的橋梁作用。在小學數學教學中，教師合理地運用直觀模型能更好地發揮幾何直觀的教學價值，促進學生更有效地理解抽象的、復雜的、混淆的、內隱的數學內容，從而提高學生的數學素養。