數形表征 猜驗遞進

王志艷 馬天紅

摘? 要：探索性學習過程中學生經歷觀察、比較、猜想、驗證等一系列活動，其中猜想驗證活動能有效促進學生學習能力、知識系統、思維的發展。教師提供的學習材料以什么形式出現？怎樣突出材料的特征才能有效促進學生提出問題、合理猜想并積極驗證呢？經過兩次不同的教學設計，筆者認為數形結合表征，逐步實現猜驗遞進更有助于學生自主探索學習。

關鍵詞：數形;猜驗;樹葉中的比;教學設計

■【教學內容】

蘇教版六年級上冊第66-67頁綜合與實踐“樹葉中的比”。

【教學片段一】觀察比較，提出問題。

第一次教學設計：

出示教材主題圖，觀察這些樹葉的形狀，你有什么想法？

預設：形狀和大小各不相同。同一種樹葉有大有小，形狀都差不多;有些不同種類的樹葉形狀也很像。

師：可以用什么描述樹葉形狀呢？討論。

第二次教學設計：

1. 認識樹葉，觀察比較。

課件出示樹葉形狀，除了呈現教材中的主題圖，還增加了樹葉拓印畫和剪影畫。

師：辨認時你是怎么想的？

2. 怎樣表示一片樹葉的形狀？

預設：長或寬，長與寬的比值。

師：用哪個數表示更合適？組織討論，鼓勵舉例子說明。

3. 介紹柳葉長、寬以及測量的方法。

師：如果計算出它們長與寬的比值，你能想到什么問題？

預設：樹葉形狀與長寬的比值之間有什么聯系？

評析：問題是數學的核心，是激發學習興趣的重要因素，而問題來自對現象的觀察與思考。第一次的設計直接呈現教材中各種各樣的樹葉：色彩豐富，形狀各異，有單生葉也有復生葉，但對于提出“用什么來表示樹葉的形狀”這一問題有干擾。學生根據已有知識經驗，自然想到用長、寬來表示樹葉形狀。老師只好尷尬地引導學生：用長、寬的比值來表征更簡便。第二次設計中，教師呈現樹葉實物圖、拓畫圖片以及剪影圖片，在觀察比較樹葉的大小形狀時凸顯了形狀的相似與不同，由此提出問題，能有效地激發學生的探究欲望。在討論的過程中，鼓勵學生用實例表達自己的觀點，用類比的方法闡述長、寬的比值是最合理的方式。數與形狀對照是研究樹葉形狀，激發數學思考的重要方法。

【教學片段二】觀察比較，引導猜想。

第一次教學設計：

師：這些樹葉長與寬的比值可能會怎樣？

預設：同一種樹葉長與寬的比值相近，不同種類的可能接近。

第二次教學設計：

1. 形狀與長和寬的比值之間有什么聯系？

預設：形狀特別的可以不研究。有的樹葉相似，長與寬的比值有沒有可能相同或相近呢？

2. 數形結合啟發思考。

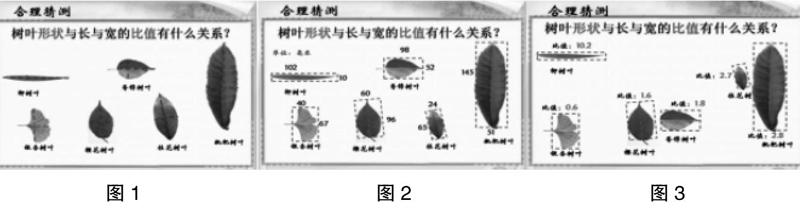
我們描出長與寬，大家算一算比值。（呈現圖1）

師：算出比值后，你能把這些樹葉分一分嗎？（呈現圖2）

出示分的結果（呈現圖3）。

師：這時，你想到什么？

根據回答依次出示——

同一種樹葉：①長與寬的比值相近？

不同種類：②形狀不同，比值不同？

③形狀相似，比值相近？

④比值越大，形狀越（? ? ）。

評析：教學中教師應努力打開文字、圖形與符號之間的通道，讓學生獲得這些不同信息之間的內在聯系，讓形象思維和抽象思維和諧共舞，促使有思維深度的數學猜想成為可能。第一次的設計在學生還沒有充分理解長寬比值與樹葉形狀之間聯系的時候，教師緊接著引導學生對比值進行猜想，顯得非常倉促。經過分析得出，學生思考形狀與長寬比值有什么聯系，需要強烈的信息刺激，使直覺易于產生作用，產生跟樹葉形狀與長寬比值相關的直接想法。所以第二次的設計，教師將研究的對象以數形結合的形式出現時，學生的已有知識和生活經驗更容易被充分調動，尤其是借助長方形的長與寬的構圖以及長與寬的具體數據來想、來猜。學生自然地經歷了從經驗中想、從知識中想、從數據中猜的過程。當然，從數據中來的猜想最有價值，也最可靠。

【教學片段三】表征數據，設法驗證。

第一次教學設計：

1. 研究同一種樹葉。

（1）算出柳樹葉長與寬的比值。

師：觀察大家計算的比值，你有什么想法？

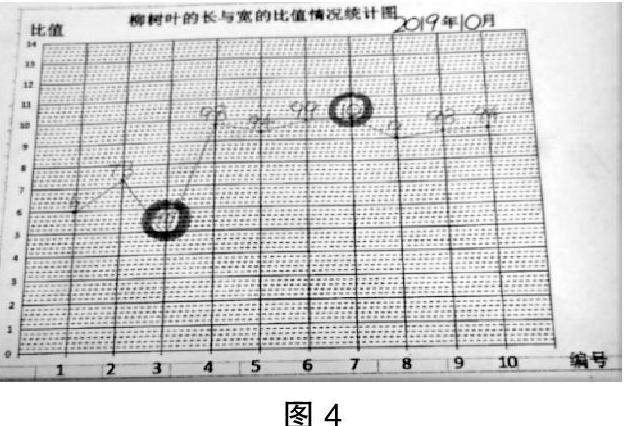
活動：把10片柳樹葉長與寬的比值制成折線統計圖，用紅筆圈出最大值，用藍筆圈出最小值（如圖4）。

思考：用哪個數來描述柳樹葉長與寬的比值更合適？（平均數）

師：算一算平均數。匯報平均值最大、最小分別是多少。

（2）比較平均數。

師：老師在電腦上用統計圖表示大家的平均值在哪個范圍。（只出示最大、最小值）

師：觀察從每一片柳葉到10片平均值的數據變化，你想說什么？（范圍變小，更集中，更有代表性，片數再多一點會怎么樣呢）

算出一組6個人的平均數。在統計圖中呈現最大值和最小值并比較。

算出全班同學的平均數，呈現在統計圖中。

問：通過計算、比較和分析，你有什么收獲？

2. 研究不同的樹葉。（略）

評析：第一次設計利用統計圖表示兩個極值，經歷從10片到60片，再到幾百片樹葉的長寬比值平均數的變化，使學生感受統計的數量越多，平均數的最大值和最小值數值越接近。這有助于發展學生的數據觀念，以尋找更合適的表示樹葉形狀的比值。一般為了促進學生研究，形狀與數值的內在聯系應該直觀外顯，可這里的數據與樹葉形狀是分割的，數據與樹葉形狀之間的內在聯系學生無法體會，導致思維活動低效，不利于發現規律，形成與猜想相應的結論。開展數學實踐活動，要使學生從多角度體驗、了解數學（如比值）的價值。課堂上教師雖適當引導啟發，有利于活動走向深入，學生的確也經歷了用動手實踐、自主探索、合作交流等方式去探索相關規律，但偏重于統計數據的比較，無論從觀察、比較還是分析的角度來看，都無法將學生的思維向數形關系的深處引導。

第二次教學設計：

1. 討論驗證方法。

師：怎樣驗證呢？

預設：測量、計算、比較。

2. 小組合作，驗證猜想。（選擇一條猜想進行驗證）

3. 交流分享。

將研究的樹葉貼出，分享：本組驗證哪條猜想？發現了什么？

形成過程性板書，如圖5。

提醒學生將樹葉實物圖按照一定的順序排列。用一個數軸（縱軸）呈現所有研究的樹葉實物圖和長寬比值。

評析：蘇霍姆林斯基說，“在人的心靈深處，都有一種根深蒂固的需要，這就是希望自己是一個發現者、探索者”，驗證猜想的活動給予學生充分自由的學習空間。小組合作既有利于學生共享樹葉資源，進行不同猜想內容的驗證，又能在驗證同一個猜想時獲得更多數據，更能體現研究對象的特點。驗證方式可以有：①舉例子，舉例子的操作核心是找到反例，如果沒有反例，那就猜對了，如果有反例就可以否定;②說理，說理可以用不同的形式進行表征，也可以進行證明等。在與學生交流分享同步進行的板書中，數據呈現也可以為學生的驗證提供更直觀的感悟：用一個數軸（縱軸）呈現所有研究對象及其分享的數據（長寬比值），通過觀察發現有的數據接近，同時將樹葉圖片也呈現在相應的位置，數形對照，驗證猜想。

總體來說，第一次教學設計，學生不能主動理解用“長、寬比值”表示樹葉形狀;學生對“樹葉形狀與長寬比值的大小之間有什么規律”的猜想比較被動。整個學習活動中，教師引導過多，學生比較盲從。修改的重點是：更換學習素材和素材呈現方式，以啟發學生提出有針對性的問題;突出樹葉與其長、寬、長寬比值的對照，采用數形結合的方式幫助學生理解、分析和猜想;舍棄統計圖的呈現方式，改用數軸的方式出示樹葉形狀與長、寬比值，讓規律看得見、說得出、想得清。

數學猜想與驗證需要每一個學生都親歷“提出疑問、大膽猜想、合理驗證、完善結論”的實踐過程，更需要教師引導學生對研究對象進行數形結合的觀察、思考、比較、計算等活動。學生建立在對物質世界直接經驗之上的真正的學習，使數學活動成為有趣的、深受學生喜愛的、能被學生理解的學科性活動。“樹葉中的比”這一“綜合與實踐”活動僅憑一片樹葉長與寬的比值，難以得出任何結論，但是當我們把多片的同種樹葉進行比較、把不同種類而形狀相似的樹葉放在一起比較、把不同種類且形狀不同的樹葉放在一起比較時，數據就會有規律，與數據相應的形狀便隨之呈現出一些明顯的有規律的現象。在材料數據從長、寬到長寬比值，再到結合數形比較和分類的過程中，猜想活動不斷推進。幾次進行猜想，經歷驗證、歸納和發現其中隱含的數學規律，是學生重要的學習手段。