淺析“幾何直觀”在小學(xué)數(shù)學(xué)教學(xué)中的運(yùn)用

陳文欽

摘 要：隨著新課程改革的不斷深入，“幾何直觀”在小學(xué)數(shù)學(xué)教學(xué)中得到了越來越廣泛的運(yùn)用。文章從分析“幾何直觀”的內(nèi)涵入手，就如何運(yùn)用“幾何直觀”開展小學(xué)數(shù)學(xué)課程中的概念、算理、規(guī)律的教學(xué)以及解決實(shí)際問題進(jìn)行闡述。

關(guān)鍵詞：小學(xué)數(shù)學(xué);“幾何直觀”;教學(xué);運(yùn)用

中圖分類號：G623.5

文獻(xiàn)標(biāo)識碼：A

“幾何直觀”是指依托、利用圖形來描述、分析和解決數(shù)學(xué)問題的一種方法。在進(jìn)行抽象的概念、算理、法則等的教學(xué)時(shí)，可以借助“幾何直觀”使問題形象化、直觀化，易于學(xué)生理解;在面對一些較為復(fù)雜的數(shù)學(xué)實(shí)際問題時(shí)，有效利用“幾何直觀”能使其變得簡單明了，使學(xué)生迅速找到解答的途徑和方法。因此，廣大小學(xué)數(shù)學(xué)教師應(yīng)研究好、運(yùn)用好“幾何直觀”，并將其貫穿于日常的教學(xué)之中。

一、深刻理解“幾何直觀”的內(nèi)涵

“幾何直觀”是由“幾何”與“直觀”兩個(gè)詞組合而成，在這里我們不妨將其分開來解析：第一，“幾何”不僅包括平時(shí)常說的幾何圖形，還包括用運(yùn)算線條、方框等直觀符號組合表示的圖示語言;第二，“直觀”并不簡單地指要使問題情境再現(xiàn)，而是要經(jīng)過提煉、概括，使問題情境數(shù)學(xué)化、形象化，通俗易懂。

二、巧妙運(yùn)用“幾何直觀”進(jìn)行教學(xué)

教學(xué)中，“幾何直觀”在概念、算理、法則的理解上，在實(shí)際問題的解決上以及其他方面都有著巧妙運(yùn)用。

1.借助“幾何直觀”理解概念

在進(jìn)行“公倍數(shù)”的教學(xué)中，為讓學(xué)生對公倍數(shù)概念有一個(gè)感性的認(rèn)識，筆者設(shè)計(jì)了這樣的情境：老鄧家中修砌了一個(gè)頂部邊長為28厘米的正方形茶臺，現(xiàn)打算在茶臺面上鋪設(shè)精致雕花瓷磚，請問在不裁切瓷磚的情況下，是選擇邊長為7厘米、邊寬為4厘米的長方形瓷磚還是選擇邊長為6厘米、邊寬為4厘米的長方形瓷磚好？課上，筆者引導(dǎo)學(xué)生把正方形茶臺面用一張正方形卡片（可同比例縮小）來表示，接著讓學(xué)生們分別用邊長為7厘米、邊寬為4厘米的長方形卡片和邊長為6厘米、邊寬為4厘米的長方形卡片進(jìn)行鋪設(shè)，在鋪設(shè)（畫圖）的過程中（如圖1、圖2），很多學(xué)生馬上就作出了使用“邊長為7厘米、邊寬為4厘米長方形的瓷磚”的正確選擇。

知其然，更要知其所以然。答案揭曉后，筆者就和學(xué)生們一起來分析和探討如此選擇的原因：28和7，28和4分別有著什么樣的關(guān)系？28和6，28和4之間分別有著什么樣的關(guān)系？得出：28是7的4倍，是4的7倍，卻不是6的整數(shù)倍。這樣就引出“公倍數(shù)”的概念。通過卡片鋪設(shè)（畫圖）的實(shí)際操作，將“公倍數(shù)”這一抽象的概念形象化、具體化，便于學(xué)生們學(xué)習(xí)和掌握。

2.借助“幾何直觀”明晰算理

在開展“分?jǐn)?shù)與分?jǐn)?shù)相乘”教學(xué)時(shí)，筆者在課程引入部分創(chuàng)設(shè)了這樣的情境：某染布師每小時(shí)染制一塊布匹的1/4， ?3個(gè)小時(shí)可以染制這塊布匹的幾分之幾？1/4小時(shí)可以染制這塊布匹的幾分之幾？

在教學(xué)中，引導(dǎo)學(xué)生畫一個(gè)長方形表示這塊布匹（如圖3），接著根據(jù)題目中的提示把這塊布匹均分為4份，很快就能得出一個(gè)小時(shí)染制的面積，即為長方形面積的1/4，再引導(dǎo)學(xué)生算出3個(gè)小時(shí)染制布匹的面積，也很直觀地得到了答案是3/4;那么1/4小時(shí)染制的面積，就是要將一小時(shí)染制的面積再均分為4份（如圖4），也就是1/4小時(shí)染制的面積，通過觀察，不難得出結(jié)果為1/16。用算式來表示就是：1/4×3= 3/4;1/4×1/4=1/16。

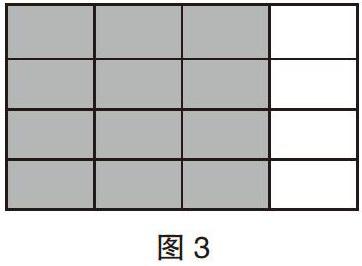
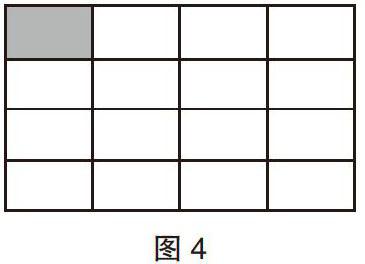
通過數(shù)形結(jié)合，讓學(xué)生動手操作，邊觀察邊思考，循序漸進(jìn)地體驗(yàn)并理解“分?jǐn)?shù)與整數(shù)相乘”的算法、“分?jǐn)?shù)與分?jǐn)?shù)相乘”的算法。

3.借助“幾何直觀”探索發(fā)現(xiàn)規(guī)律

在進(jìn)行“圓柱表面積”的教學(xué)中，筆者將一個(gè)易拉罐（去底和蓋后）沿著側(cè)面某垂直于底面的直線剪開，不難發(fā)現(xiàn)，被剪開的易拉罐側(cè)面展開并被拉平后是一個(gè)長方形。通過觀察，讓學(xué)生理解長方形的長和圓柱底面的周長之間、長方形的寬和圓柱高之間分別存在著怎樣的內(nèi)在關(guān)系。在進(jìn)行“圓柱體積”的教學(xué)中，筆者借助“圖形直觀”引導(dǎo)學(xué)生把一個(gè)圓柱體沿著其頂面圓心進(jìn)行偶數(shù)多等分切割，將切下的扇形進(jìn)行拼組裝，得到了一個(gè)類長方體。通過引導(dǎo)，學(xué)生們結(jié)合之前已掌握的長方體的體積計(jì)算方法，就很自然地推導(dǎo)出圓柱體體積的計(jì)算公式。

4.借助“幾何直觀”解決實(shí)際問題

運(yùn)用“幾何直觀”能在解決人們實(shí)際生活中遇到的問題中發(fā)揮積極作用，這也是我們學(xué)習(xí)數(shù)學(xué)的初衷。如某農(nóng)場有一長100米、寬70米的牧場，隨著養(yǎng)殖規(guī)模的擴(kuò)大，準(zhǔn)備在原牧場的基礎(chǔ)上進(jìn)行擴(kuò)建，規(guī)劃中的新牧場的長為118米，寬為82米，那新牧場的面積比擴(kuò)建前增加了多少？在該問題的求解過程中，筆者引導(dǎo)學(xué)生用畫圖的方法進(jìn)行分析，首先把牧場抽象為一個(gè)長方形，同比例進(jìn)行縮小，畫好新牧場后，也將原牧場的位置標(biāo)出（如圖5、圖6）。

從圖上不難看出，牧場擴(kuò)建后增加的部分面積其實(shí)就是圖6中的標(biāo)記為a，b，c三個(gè)部分面積之和，這就迅速找出了計(jì)算方法。因此，在計(jì)算比較復(fù)雜的實(shí)際問題時(shí)，可以借助幾何圖形，發(fā)現(xiàn)問題的本質(zhì)，并快速解決問題。

總之，“幾何直觀”在小學(xué)數(shù)學(xué)教學(xué)中的作用在實(shí)踐中已越來越多地被教育界所認(rèn)可，我們在進(jìn)行數(shù)學(xué)教學(xué)過程中應(yīng)更多地運(yùn)用并教會學(xué)生運(yùn)用“幾何直觀”的方法和思維來解析題意、明晰思路、解決問題，讓學(xué)生理解更深刻、透徹，讓課堂教學(xué)更輕松、高效。

參考文獻(xiàn)：

[1]趙芳英.幾何畫板在小學(xué)數(shù)學(xué)教學(xué)中的應(yīng)用探討[J].教育觀察（下半月刊），2017（5）.

[2]王莉莉.淺談培養(yǎng)小學(xué)生幾何直觀能力的幾點(diǎn)做法[J].基礎(chǔ)教育論壇，2016（1）.

[3]黃愛華.課堂需要深度對話[J].小學(xué)教學(xué)設(shè)計(jì)，2016（5）.

[4]王全勝.淺議數(shù)學(xué)教學(xué)中兒童觀察能力的培養(yǎng)[J].讀與寫（下旬刊），2010（9）.