三談“好玩”的五角星

哈爾濱師范大學研究生 馬正方

三談“好玩”的五角星

哈爾濱師范大學研究生 馬正方

本文以五角坐標系為導向，以兩個定律為走向，揭示五角星好玩的內在美，并且說明五角坐標系可成為素質教育的好教材。

定律；五角坐標系；等式；星羅數布；內在美

實現數學強國的中國夢，就不可缺少數學理論的創新！“厲害了，我的國”，厲害起來吧，中國的數學！

【定律1】如圖1所示，把任何十項的自然數列a1、a2、a3、a4……a10按一定次序安排在五角星的十個兩線交點上：（a7+a8）2-（a4+a10）2=b1，（a6+a7）2-（a1+a9）2=b2，（a10+a6）2-（a3+a8）2=b3，（a9+a10）2-（a5+a7）2=b4，（a8+a9）2-（a2+a6）2=b5；b1+b2+b4+b5=4 b3。如果星角內的某個數是平方數，便能夠構成勾股弦數。

圖1

例1：如圖2所示，把十項的自然數列1、2、3……10按一定次序安排在五角星的十個兩線交點上：

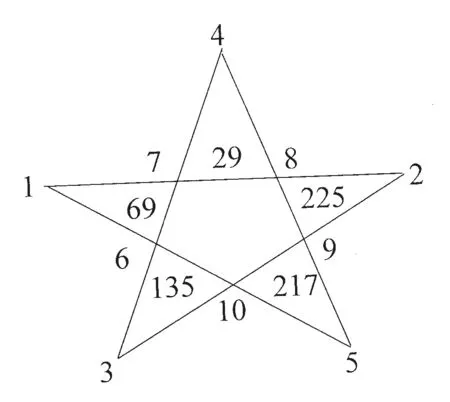
圖2

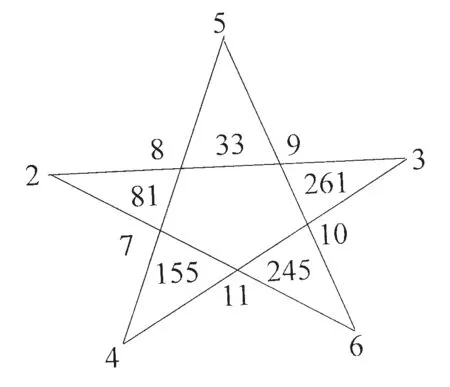
圖3

如圖2所示，（7+8）2-（4+10）2=29，（6+7）2-（1+9）2=69，（10+6）2-（3+8）2=135，（9+10）2-（5+7）2=217，（8+9）2-（2+6）2=225，從而可以寫成和諧的等式：29+69+217+225=4×135。由于星角內的225是平方數152，又由于225是“172-82”的差數，即172-82=152，從而該等式能夠構成勾股弦數：82+152=172。

例2：如圖3所示，把十項自然數列2、3、4……11按一定次序安排在五角星上：如圖3所示，（8+9）2-（5+11）2=33，（7+8）2-（2+10）2=81， （11+7）2-（4+9）2=155，（10+11）2-（6+8）2=245，（9+10）2-（3+7）2=261，從而可以寫成和諧的等式：33+81+245+261=4×155；由于星角內的81是平方數92，又由于81是“152-122”的差數，即152-122=92，從而該等式能夠構成勾股弦數：92+122=152。

【定律2】如圖4所示，把任何十項的等差數列a1、a2、a3、a4……a10按一定次序安排在五角星的十個兩線交點上：（a7×a8）-（a4×a10）=b1，（a6×a7）-（a1×a9）=b2，（a10×a6）-（a3×a8）=b3，（a9×a10）-（a5×a7）=b4，（a8×a9）-（a2×a6）=b5；（b1+b2+b4+b5）-4 b3=20x2，x為該等差數列的公差。

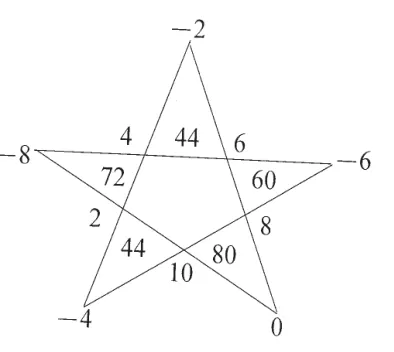
圖4

例3：如圖4所示，（4×6）-［（-2）×10］=44，（2×4）-［（-8）×8］=72，（10×2） -［（-4）×6］=44（ 即b3），（8×10） -（0×4）=80，（6×8） -［（-6）×2］=60，從而寫成和諧的等式：（44+72+80+60）-（4×44）=20×22，底數“2”為該等差數列的公差。

數學是宇宙的語言，數學具有獨特的深刻性和哲理性。本文是第三次談論“好玩”的五角星。在“大眾創業，萬眾創新”的號召鼓舞下，“五角坐標系”（如圖1所示）應運而生了！五角坐標系可以充分表達五角星的內在美！從往昔的直角坐標系到如今的五角坐標系，能否說是數學發展的里程碑呢？星羅數布亮閃閃，五角坐標理當然。簡明高效易操作，有趣好玩開眼簾。素質教育好教材，數學文化新亮點。數學世界新景點，留戀難舍動心弦。星羅數布亮閃閃，星星之火可燎原。其中不足待完善。敬請恩師多指點！

五角坐標系可簡稱“幻星”，顧名思義就是“變幻多端之星”！對“幻星”精心設計出有條不紊的運算程序，完全可以得出許許多多的豐富多彩的數字結果來。幻星是數學王國的明星，是一座數學的富礦，期待有識之士進行“追星”開發！似乎夸張地說：本文所列舉的兩個定律對幻星來說只是“昆侖山上一棵草，九牛背上一根毛，滄海橫流一滴水，億萬富翁錢一角”！幻星啊幻星，變幻的載體，數學的精靈；宇宙的語言，陰陽的化身；精神的旅游，心靈的美食；素質的教材，智力的天使；夢想的熱土，美妙的領地；數形的默契，和諧的演義。

欲做“人前星”，可做“星”前人！