“一題多解”突破難點

陸劍雪

摘要：教學實踐與思辨表明，重視微觀方面的教學設計是實現數學有效教學的充要條件，而一題多解是微觀教學設計的重要思維訓練形式。通過不同形式的自主學習、探究活動，讓學生經歷數學問題從發現到解決的全過程，注重引導學生從多種解法中解決難點，找出最簡捷、最巧妙的解法，體驗成功的喜悅，培養良好的思維習慣，提高學生思維的品質，體會數學思想方法，享受數學學習的快樂，形成并發展創新意識。

關鍵詞：一題多解；知識脈絡；創新意識

中圖分類號：G633.6 文獻標識碼：A 文章編號：1992-7711（2016）07-0021

所謂“一題多解”，是指通過不同的思維途徑，采用多種解題方法解決同一個問題的教學方法。二十多年的教學實踐與教學反思總結都表明，一題多解不僅是激發學生興趣、開拓思路、提升思維品質、靈活應變，讓學生形成解決問題能力的基本策略，而且能讓學生體驗解決問題時策略選擇的多樣性，發展他們的實踐能力與創新能力。本文擬就一題多解在初中數學教學微型設計中的應用，做一些課堂有效教學的實踐和探索。

一、設計一題多解，打開數學大門

在由簡入繁、循序漸進的數學殿堂中，每一領域都有一扇虛掩的大門，等待我們去開啟。七年級學生剛學幾何的推理論證時，總會很不習慣。這是由于幾何所研究的對象、過程、思維方式、語言的表達都與代數有較大的區別，并且幾何語言是人們從長期的實踐中提煉而成的，具有概括性、抽象性、邏輯性較強等特點。為此，面對問題，如果能引導學生從不同的角度去思考，就能把學生的好奇心轉化為求知欲，讓他們興致勃勃地去推開幾何殿堂的大門。

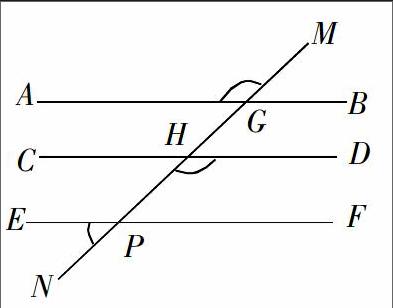
例題：如圖所示，直線MN分別和直線AB，CD，EF相交于點G，H，P，∠1=∠2，∠2+∠3=180°，試問：AB與EF平行嗎？為什么？

分析：首先，掃除三線八角中的同位角、內錯角、同旁內角幾何入門的第一道門檻，總結三類角的特點，關鍵先找“截線”，再把復雜圖形基本化（F形、Z形、U形），運用定義識別。然后分析要想得到AB∥EF，可以從問題的結果出發，思考學習過的判斷兩條直線平行的方法有哪些，讓學生回想學過的五種方法，也培養學生思維的流暢性，并滲透分析法。需滿足條件∠1=∠EPM，或者∠AGP=∠GPF，或者∠AGP+∠GPE=180°，或者（利于平行的傳遞性）先證AB∥CD，再證CD∥EF，所以可得AB∥EF。因此，這四種方法進行解答，并且四種方法靈活運用。還有平行線定義：在同一平面內不相交的兩條直線叫做平行線，平行線的定義法一般不常用。

解：AB∥EF，理由

方法1：

∵∠1=∠2 ∠2+∠3=180°（已知）

∴∠1+∠3=180°（等量代換）

又∵∠3+∠EPM=180°（鄰補角定義）

∴∠1=∠EPM（等式性質）

∴AB∥EF（同位角相等，兩直線平行）

方法2：

∵∠3=∠MPF（對頂角相等）

∠2+∠3=180°（已知）

∴∠MPF+∠1=180°（等量代換）

又∵∠1=∠2（已知）

∴∠1+∠MPF=180°（等量代換）

又∵∠1+∠AGP=180°（鄰補角定義）

∴∠AGP=∠MPF（等式性質）

∴AB∥EF（內錯角相等，兩直線平行）

方法3：

∵∠1=∠2 ∠2+∠3=180°（已知）

∴∠1+∠3=180°（等量代換）

又∵∠1=∠BGP ∠3=∠GPF（對頂角相等）

又∵∠BGP+∠GPF=180°（等量代換）

∴AB∥EF（同旁內角互補，兩直線平行）

方法4：

∵∠2=∠CHM（對頂角相等）

∠1=∠2（已知）

∴∠1=∠CHM（等量代換）

∴AB∥CD（同位角相等，兩直線平行）

又∵∠3=∠HPF（對頂角相等）

∠2+∠3=180°（已知）

∴∠2+∠HPF=180°（等量代換）

∴CD∥EF （同旁內角互補，兩直線平行）

∴ AB∥EF（如果兩條直線都和第三條直線平行，那么這兩條直線也互相平行）

此例中，一看到探究平行線，馬上想起一系列角的等量關系，這種條件反射的建立，是最基本的數學素養之一。一題多解表現為依據定義、定理、公式和已知條件，思維朝著各種可能的方向擴散前進，不局限于既定的模式，從不同的角度尋找解決問題的各種途徑，培養學生的發散思維能力。在此，一題多解也讓學生享受了成功的喜悅。適時的引導啟發也讓學生感受到學習幾何有趣、不難。

二、運用一題多解，驅散畏難情緒

領進數學大門，是成功的第一步。但客觀地說，數學的確有不少難題，甚至在一些同學看來，這些難題簡直是一座座不可逾越的大山。所謂“難者不會”，如何通過一題多解的教學設計驅散畏難者的消極情緒，幫助他們重拾信心，變成“會者不難”，是我們要研究的另一大課題。

小學解應用題，學生學了五、六年的算術解法，已經習慣于算術法，是逆向思考；而初中解應用題，學生學習列方程法，是正向思考，思路上不一定轉得了彎。盡管強調：列方程解應用題要求“分析題意、找出等量關系、據此列出方程”，但這種強調對于初學者來說，把等量關系復雜化了，常常是一旦思維受阻，就一籌莫展，易產生畏懼心理。

為此，列方程的實質說成：在題目描述的過程中，先隨便“拉出”一個量，根據題意用兩種不同的方法表示“它”，中間用“等號”連接，方程即列成。這樣，若能進行策略開放，經常對一些問題從不同角度思考，得出多種解法，可以幫助同學們開拓思維。再遇思維受阻時，進行換位思考，便也能茅塞頓開，拿出解題策略，勢如破竹，使學生感到列方程是唾手可得的事情。

最后，歸納出列方程解應用題的解題方法，若一量為所求量（設為未知數），另一量給出的數值較具體，則選擇第三量列出方程，即一量設，一量已知，一量列方程。這使學生在解應用題時思路更明確清晰，從而能快捷地列出方程。

列方程解應用題，是整個初中數學教學的重點，也可以說是難點。因此，起始課教學讓學生掌握好它的原理、方法及實質則顯得十分重要。教學設計要符合初中生的認知水平，一個合適量的“拉出”，衍生了問題的一系列的不同解法，同時，歸納出列方程解決實際問題的一般步驟，使學生的思維始終處于活躍狀態。他們不僅充分利用已知解決未知，并且在解決未知的過程中，有效地拓展了思維，有利于培養學生的發散思維，從而培養和提高學生分析問題、解決問題的能力。

有了成功的嘗試，學生再次見到難題就會從容得多、自信得多。當然，這種“成功”一定是學生經過努力體驗到的“成功”，而不是看教師演示出的“成功”。

三、掌握一題多解，融通知識脈絡

許多章節的教學目標中都有“熟練掌握”基本知識的要求，與此相配套的強化訓練往往會形成思維定勢。思維定勢固然有其積極的意義，但也會產生消極作用，表現為思考問題常常傾向于某種固定的模式，思維不夠靈活。所以，尋求多種解題方法，有助于消除思維定勢的消極作用，使所學知識融會貫通、形成體系，便于活學活用，爭取更大的進步。

在不同的教學階段，證明同一個命題的方法越來越優化，這不僅能幫助學生克服思維定勢，而且有助于學生更好地把握知識的脈絡。

尤其有效的是在數學復習課上，善于多方位思考，探究一題多解，最有利于學生掌握和鞏固知識，把已經差不多遺忘的知識點重新建立起來，挖掘問題的內在聯系，向“縱、橫、深、廣”拓展，向“少、精、活”探索，既能提高解題速度，又能有目的地把各類知識串聯起來，達到溫故而知新的目的，逐步提高認知的層次，從低級到高級的螺旋式上升，實現一題多解意義的延伸。

四、尋求一題多解，培養創新意識

人才的培養不只是讓他們掌握已有的知識技能，更高的目標在于培養他們的創造能力和創新意識。在教學實踐中，注重產生結論的過程教學，引導學生探索一道題目的多種解法，既可以增強學生解題的信心，激發學生的學習興趣，又可以培養學生的創新意識。要做到一題多解，教師就要利用典型、生動的事例激發學生的“求異動機”，有意識地安排一些靈活多變的練習，在引導學生掌握了基本的、規律性的解題思路的同時抓住各部分知識間的聯系及方法間的聯系，進而引導學生從不同角度、不同領域去探索解題方法。

為了尋求一種新的解（證）法，學生往往冥思苦想，反復琢磨，百思不得其解。可一旦領悟，解（證）法卻又那樣出人意料。通過尋求新的解（證）法，學生既體驗到“山窮水盡疑無路”的艱辛，又品嘗到“柳暗花明又一村”的驚喜，從而激起他們更加強烈的學習熱情。有的同學課后繼續探究新的解題方法，由被動轉為主動，從厭學變為樂學、好學。相信以后再遇到其他題目，他們也會不滿足于一種解法，不斷尋找最簡捷、最巧妙的解法，通過各種不同形式的自主學習、探究活動，學生體驗數學問題從發現到解決的全過程，享受成功的喜悅，并能從中形成、強化創新意識。

借鑒前人理論可知，解法探究作為數學有效教學的重要途徑，就是要讓學生在獲得數學知識的同時，改進學習方式、方法，既善于聽講，又適應變式、樂于探究，從而使興趣得到培養、情操得到陶冶、智力得到開發、素質得到提高，從根本上促進學生的進步和發展。

二十多年的基礎課堂教學實踐又證明，一題多解的教學微設計要求教師做好引導啟發，同時竭力鼓勵學生主動思考、積極探索，可以促進學生經歷知識產生的過程，理解并且掌握基礎知識、基本技能及其應用，感悟并熟悉數學思想方法，學生學得更明、更好、更深；可以促進學生學會了好的思考方法，提升了學習能力，達到了不需要教的境界，學生學得更多、更快、更強。

數學課堂有效教學的實踐和探索還在不斷深入，而一題多解的教學設計將永不落幕。它會不斷散發出神奇的魅力，感召我們的數學課堂探微知著，一探到底。

（作者單位：江蘇省蘇州市吳江區蘆墟初級中學 215200）