培養初中生數學問題意識的方法

陳云雷

摘要：問題意識是指人們在認識活動中遇到疑惑的以解決的實際問題所產生的一種懷疑、困惑、焦慮、探究的心理狀態。這種心理狀態能促使人們積極思考。本文從教學實踐出發，提出幾點培養學生問題意識的方法。

關鍵詞：數學教學；問題意識；創新力；途徑和方法

中圖分類號：G633.6 文獻標識碼：A 文章編號：1992-7711（2016）02-0030

一、引言

問題是數學的靈魂所在。問題意識是指人們在認識活動中遇到疑惑的以解決的實際問題所產生的一種懷疑、困惑、焦慮、探究的心理狀態。這種心理狀態能促使人們積極思考，不斷提出問題、解決問題。問題意識一旦養成，學生對知識就不會滿足于表象，就會對觀察到的現象產生疑問，進而產生一種內驅力去解決問題。愛因斯坦曾說過：“提出一個問題遠比解決一個問題更重要。”

新課程改革明確指出了問題意識在數學教學中的重要性。《數學課程標準》提及到關于數學課程的總體目標：“要使學生初步學會從數學的角度來提出問題、理解問題，能綜合運用所學來解決問題，發展應用意識。要做到知識與技能、數學思考問題、解決問題、情感態度四方面的緊密結合，充分培養學生的問題意識，提高學生解決問題的能力。”新課程要求學生多動手、多交流、多合作，浙教版初中數學教材中也充分體現新課改的要求，設置了“做一做、想一想、議一議”等環節，為學生問題意識的培養提供了啟發性的素材。因此，初中數學教師要在教學過程中注重對學生學會思考、學會提問的引導，讓學生自主探究、提出問題，培養學生敢于懷疑、敢于探索的精神，提高其思維的深刻性、獨特性和批判性。

二、培養學生問題意識的方法

針對現在初中數學教學過程中學生問題意識普遍不強的現狀，響應新課程改革的號召，跟隨教育改革步伐，數學教師需要在教學過程中對學生問題意識的培養予以關注和思考，更新教學理念，改變傳統教學方式，結合教材內容多方式地來培養學生發現、提出問題的能力。筆者從多年的教學實踐出發，談一談初中數學教學中培養學生問題意識的有效途徑和方法。

1. 樹立問題意識，讓學生懂得提問

問題是數學的心臟。學習從提問開始。沒有疑問就不會有思考和探索，更談不上科技的創新。有了問題，才會產生對一個現象無止境的研究探索，讓思維得到高速運轉，在這個過程當中，學生所學到的知識和技能也能得到激活，生理和心理技能得到調動，提高學習的效率和質量。讓學生知道提出問題對于學習的重要性，樹立提出問題重于解決問題的意識。

案例1：《相似三角形的應用》

例：正午，九年級1班同學測得校門口的路燈桿子的影長為6米，在同一時刻里，他們測得身高1.6米同學的影長為1.2米，求該路燈桿子的高度是多少米？

生：設該路燈桿子的高度為x米，可列方程x/6=1.6/1.2，解得x=8。

師：你為什么這樣列方程，依據是什么？

生：太陽光是平行光，在平行光的直射下，物體的高度與影長成正比。

師：用這樣的方法測量物體的高度，任何時候都可行嗎？

生：沒有太陽，下雨天，發大水，晚上，沒有月亮的時候，就不行。

師：你們能結合具體情況，提出關于測量物高的一些問題嗎？

生：晚上怎么測物體的高度？

生：霧霾天氣怎么測物體的高度？

生：陰天怎么測？ ……

師：很好，這么多的問題，我們這節課就選擇在晚上如何測量路燈桿子的高度，晚上雖然沒有太陽光，但是還有燈光，所以我們就把在晚上沒有路燈桿子的高度作為本節課的學習內容。

說明：本案例中，教師設置平行投影中的問題情境，為運用相似三角形解決問題作鋪墊，在此基礎上，讓學生提出各種問題，教師在梳理這些問題時，很自然地引出本課要研究的內容。

2. 針對學生心理，讓學生敢問

心理研究表明，學生對未知的內容都有一種好奇的心理。越是疑難的問題，他們研究興趣越濃。因此，在課堂上，教師要設法創設一些問題，以吸引學生的興趣。讓他們想問、敢問。讓他們主動、生動地學習，從而保持一種強烈的好奇心和探究精神。

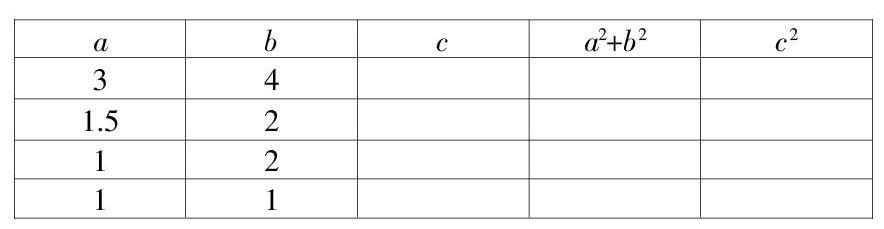
案例2：探索勾股定理

觀察圖形

正方形A中含有____個小方格，即A的面積是____個單位面積；正方形B中含有____個小方格，即B的面積是____個單位面積；正方形C中含有____個小方格，即C的面積是____個單位面積；

當課堂完成第一環節“觀察圖形”后，得出32+42+52的結論。于是有部分學生馬上推論出直角三角形的三邊關系：a2+b2=c2。

這時，教師指導學生進行探究，是否所有的直角三角形都符合這一規律，同學們會有哪些疑問？

生1：假如直角三角形的三邊不是整數，是否也符合a2+b2=c2的規律？

生2：如果上面的三角形三邊擴大n倍，是不是也符合呢？

生3：符合這一規律的直角三角形，跟角的大小是不是有關系，比如，兩個一個是30°，還有一個是60°，或者兩個都是45°，或者不是特殊角，它們是否也是符合a2+b2=c2。

生4：凡是符合a2+b2=c2這一規律的是否都是直角三角形？

……

師：好，那接下來，我們就通過不同的途徑和方法，來驗證這一規律。

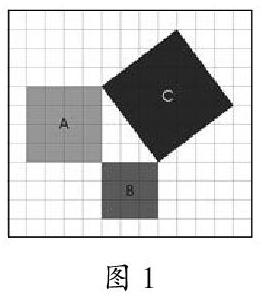
問題：在紙上畫出四個直角三角形，使其兩條直角邊邊分別為3 cm他4cm，1.5 cm和2 cm，1 cm和2 cm，1cm和1cm，分別測得這四個直角三角形的斜邊的長，并填寫下表。

分析：由于學生剛學勾股定理，對其中三邊之間的關系會感到非常神奇，因而疑惑也特別多。教師以學生提問為出發點，讓學生動手畫不同數值的直角三角形，通過畫直角邊為小數的值，就將探究活動進一步深化，學生體會到由特殊到一般的規律也將更加深刻。

3. 巧用錯誤資源，讓學生會問

錯誤是學習過程中的必然產物，有時利用學習過程中的錯誤，引導他們從中發現問題、提出問題，并解決問題。之所以有錯誤，就是因為學生在此有困惑。因此也就有必要在這些地方多問幾個為什么。

案例3：一次函數圖像

問題：已知等腰△ABC的周長為18cm，求底邊（cm）與腰長（cm）的函數關系式，并畫出函數的圖像。

當筆者用PPT呈現出來的時候，很多學生都能給出正確的答案。于是也順勢給出自己的答案，如圖2所示。這時有些學生也都認可了這樣的答案。

這時，一位學生舉手示意，他提出這樣的一個問題：根據題意，自變量的取值范圍不能為負數。

生2：是啊，負數不行，但是也不能等于9。”另一個學生提出要求自變量的取值范圍。

生3：還要考慮三角形兩邊之和大于第三邊。

生4：那圖像就不是一條直線了。

師：那同學們綜合考慮這些因素，試著求自變量的取值范圍，并在坐標系里畫出函數的圖像。

在師生互動交流中，學生很快就得出正確答案

分析：本題求等腰三角形底邊與腰長的函數關系式，相對來說還是比較容易的。真正難點在于求自變量的取值范圍。學生最容易忽略的往往是根據自變量的取值范圍，來確定函數圖像是直線、射線還是線段。課堂上，筆者故意給出一個錯誤的答案，設置一個陷阱，讓學生自己提出問題，自己解決。從而培養學生關于思考、關于質疑的良好品質。

4. 創設問題情境，讓學生樂問

一個良好的問題情境，能將學生引入到思維高度運作，積極探索解決問題的情境中，極大地挖掘學生的潛能，促使學生不斷去思索、探究解決問題的方法，并在探究中不斷地形成問題意識，去疑惑、去質疑。讓學生集中注意力，學會學習，樂于學習，增強學習的趣味性和有效性。創設問題情境可采取多種多樣的方式，如教師可以精心設置適當的懸念、情境，為學生創設急需解決的問題，讓學生產生認知沖突，激起學生的好奇心，形成強勁的學習動力。讓學生在驚奇、詫異、憤懣的心理狀態下主動去觀察、猜測、估計、試驗，在不斷的發現矛盾的過程中提出質疑和自我見解，讓學生體驗到發現問題的樂趣，培養學生樂于發現、提出新問題。

例如，在進行“用字母表示數”時，筆者在上課之前就給學生安排了這樣一個小游戲，讓學生把自己的出生月份先乘以2，再加5的和再乘以10，最后再讓其加上家里的成員數目，將所得結果告訴教師，教師很快就能說出學生的出生月份和家里成員數目。學生在這個時間瞠目結舌于教師的“智慧”，并且對于如何快速得出答案充滿好奇。這時，連平時很不愛提問的學生都想測試教師說的是否準確，并樂于問教師這是為什么？此時，筆者趁熱打鐵，告訴學生，學會了“用字母表示數”這一節內容他們也可以變這個神奇的魔術，這樣不但激發了學生的興趣，也激發了學生的求知欲，并培養了學生樂問的意識。

三、結束語

學生提出一個問題比教師直接告訴他們的一個定理價值更大、意義也更深遠。數學教師在教學過程中，要給學生提出問題留有足夠的時間和空間，充分發揮學生的學習主體地位，對不同學生提出的不同層次的問題堅持以鼓勵為主，及時做出評價。培養學生的問題意識切忌急功近利，而要逐步、逐漸地進行培養。在教師更新教學理念的基礎上，全面把握教材，并在課堂內外始終讓學生的大腦思維處于激活和開放的狀態，加強對學生問題意識的培養。

（作者單位：浙江省樂清市仙溪鎮福溪學校 325600）