“效”可以“問”出來

張波

【摘要】課堂提問是數學教學中不可缺少的重要手段，是師生交流的主要形式.新課程理念下的初中數學課堂教學，教師是組織者，引導學生在獲取數學知識的過程中能積極主動地去感受、探究數學問題，從而獲得數學認知能力和創新能力.這其中，教師的有效提問就起著關鍵的“導向”作用.本文就“初中數學課堂有效提問設計的原則”從設問、表述、難度、層次、興趣、創新等六個方面來闡述筆者在教學實踐中的一些粗淺體會與做法.

【關鍵詞】初中數學；有效提問；設計原則

數學課堂中，有效提問是教學的關鍵，它不僅可以展現教師和數學的無形魅力，還可以讓學生在廣闊的思維宇宙中自由飛翔.“水本無華，相蕩乃成漣漪； 石本無火，相擊而發靈光.”打造高效數學課堂，也需要這樣的“漣漪”和“靈光”，把握課堂有效提問設計的原則，巧妙提問，從而在創造性的頭腦風暴中，活躍課堂氣氛激發個體思考，啟迪師生心智，提高課堂教學效率，促進學生健康發展

一、精心設問

教師要縝密考慮預設問題的基點.一個設計得好的問題既能激發學生對數學內容的學習興趣，調動他們思考、解決問題的積極性，也可以引導學生的思考方向，擴大思維廣度，提高思維層次，同時也有利于學生間的相互啟發，促進師生間的交流.因此，課前縝密考慮問題的預設是實現有效數學教學的必要前提.為了保證課堂教學的有效性，教師必須明確所提出問題的目的.要明確每一個的問題的具體目的，是為了引起學生的學習興趣、檢查學生對已有知識的記憶，還是啟發學生進行進一步的思考等等.教師要在備課時作出充分的考慮，否則在課堂上隨機的發問，就會出現一些無效的問題，浪費寶貴的課堂時間.

例如：在講授新課：“不在同一直線上的三點確定一個圓”.

問題1：過一點可畫多少個圓？為什么？

問題2：過兩點可畫多少個圓？圓心的位置有什么規律？為什么？

問題3：過不在同一直線上三點A，B，C畫圓，這樣的圓要經過A，B，圓心在哪里？這樣的圓又要過B，C，圓心在哪里？若同時經過A，B，C，圓心又在哪里？

問題4：這樣的圓可畫多少個？

教師單刀直入、層層設問、簡單明了，學生動腦、動手，把自己作為“研究者”，逐步深入，將已有的知識、思維方法遷移到新知識中去，學得輕松，記得也牢.

二、表述準確

有效課堂提問的問題需表達清楚、簡潔明了、無重復性，問題的水平與學生的知識水平相符.學生必須通過思考才能回答，教師的語調和其他肢體語言能充分的利用來促進學生的思考.教師能從學生的認知水平出發，以學生易于理解的語言來闡述問題，從學生的反應看，學生基本上都能很好的理解教師的問題.

例如：著名特級教師李庾南在講解《因式分解》這節課時，描述因式分解的概念是和整式的乘法進行對比，說了很多遍的“反過來”.這是多么好的一句“白話文”，卻是李老師“苦心經營”的一句話.很多老師在講解因式分解概念時總是按照教材中的概念描述：把一個多項式化為幾個整式的乘積的形式.學生對這里的“化為”也是一知半解，導致分解時總出現分解不徹底等現象.學生剛學完整式的乘法，緊接著就學習因式分解，必然受到思維定勢的影響，搞不清二者的區別于聯系.李老師的一句“反過來”，通俗易懂，學生樂于接受.例如，教學“異分母分式加減法”，引入1x+2-1x-2后提問：“1x+2，1x-2 這兩個分式有什么特點？”顯然，這一提問不準確，學生回答：“分子都是1”，顯然是正確的，但回答沒有達到教師的提問意圖.如果改問：“這兩個分式的分母相同嗎？分母不同的分式能不能直接相加？為什么？”這樣的提問既明確，又問在關鍵處，有助于學生理解為什么要通分的道理.

三、難度適中

教師在設計提問要把握好問題設計的難度，避免兩類提問：一類是太簡單，一類是太難.根據實際情況適當的調整使得問題的難度符合學生的認知水平.

有的教師喜歡問學生一些答案是顯而易見的問題，比如“今天星期幾？” “這個問題很顯然是——對的”.這種問題不論是讓全班齊答 ，還是讓某個學生回答 ，都是很無聊的.此類問題問的太多，而且又面向全體學生 ，容易會使學生反感 ，思維懈怠.

反之難度太高的問題教師要嚴格控制，在課堂上要根據學生的反應適時調整，設置一些過渡性的問題，是學生順利越過思維障礙的門檻.蘇科版九下教材中有這樣一道習題：如圖，用一段長20 m的鋁合金型材制作一個矩形窗框，窗框的長和寬各為多少時，該窗的透光面積最大（精確到0.1 m，且不計鋁合金型材的寬度）？

用較少的材料制作透光面積盡可能大的窗框，是生活中常見的優化問題之一，也是利用二次函數探究與幾何圖形有關的最大值問題.本題如果直接拋給學生，不易解答.筆者在講解這道題目時采用了化零為整、由易到難的方法，通過一組有梯度的問題，既降低了難度，又讓不同層次的學生都有回答的機會，又讓學生對已掌握的知識進行梳理分析，透過問題看清本質.

師：用20米的鋁合金型材圍成一個矩形窗框，如圖，有幾種制作方法？什么時候面積最大？

生1：無數種，圍成正方形面積最大.

師：現在要在中間加一根鋁合金EF，設AB=x，則AD等于多少？

生2：AB=20-3x2.

師：當x為多少時，這個窗框是一個正方形？

生2：x=20-3x2，x=4.

師：你們也是這么做的嗎？

生3：20÷5=4，邊長為4.

師：好方法，不用解方程，直接求得邊長.此時面積是多少？

生3：16.

師：當AD為多長時，窗框的面積是16 m2？

生4：4

生5：可能還有一個答案.

師：請你試試

生5：x·20-3x2=16，解得x1=4，x2=83.當AD為4或83時，窗框的面積是16 m2

師：窗框的面積能達到17 m2嗎？如何列方程？

眾生：x·20-3x2=17

師：你有什么想法？

生6：不可能是17.

師：為什么？

生6：因為正方形時面積最大.

師：超過16不可能嗎？

生7：可能.因為中間有一條.

師：正是由于中間加了這條導致并不是正方形時面積最大，來試試17有沒有可能.化簡后得3x2-20x+34=0，b2-4ac0，方程沒有實數根.還有其他解法嗎？

眾生：（沉默）

師：16.9，16.8，16.7？有方法嗎？

生8：可以求最大值

師：非常好！請同學們動筆來算一下

學生很快得到x·20-3x2=-32x2+10x=-32x-1032+503，最大值為503.

四、層次清晰

數學學習具有高度的抽象性，初中生雖已形成了形式運演思維，具有一定的抽象思維能力，但面對新知識的學習、陌生的任務，他們常常還是要借助具體事物的支撐.所以教師設計的問題要有層次性，應該體現思維發展的要求，教師要緊扣教材的重點難點，分析教材內容的內在聯系、邏輯順序，按照由具體到抽象，由已知到未知，由感性到理性的認知規律，由易到難，由簡到繁，循序漸進的設計問題，是學生的認識逐漸深入，提高.

再次學生是學習的主體，由于智力發展水平及個性特征的差異，不同的學生對同一事物的理解角度和深度必然有明顯的差異.有很多教師偏向于設置有一定難度的問題，常提問成績較好的學生，這樣學習能力弱的學生就會感受到被冷落，久而久之，就會失去學習的興趣與信心.因此，在課堂教學中，教師必須考慮學生的差異性，在問題設計方面要考慮學生水平的層次性，對不同程度、不同學習能力的學生提出不同的問題，這樣既能符合學生的思維特點，又能讓每一個學生都能有機會參與到課堂學習中.

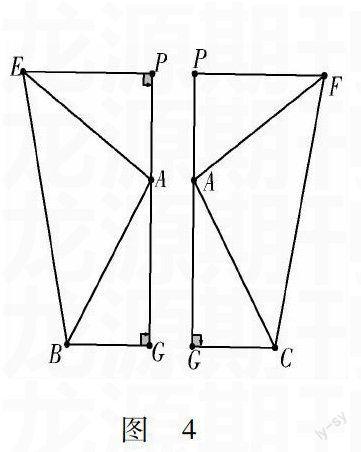
如圖1，△ABC中，AG⊥BC于點G，以A為直角頂點，分別以AB、AC為直角邊，向△ABC外作等腰Rt△ABE和等腰Rt△ACF，過點E，F作射線GA的垂線，垂足分別為P，Q. 試探究EP與FQ之間的數量關系，并證明你的結論.

問題1：這個圖形中有你熟悉的幾何圖形嗎？

分析：這個問題比較基礎，而且是一個開放性的問題，可以讓第四類學生（理解能力弱、被動回答）來回答，學生很容易找到Rt△APE、Rt△AGB 、Rt△AGC 、Rt△AQF、等腰直角三角形EAB，等腰直角三角形FAC.

問題2：這些圖形之間有什么關系嗎？（學生容易考慮到三角形全等，但是由于此圖形較復雜，不容易找出其中的對應關系.此時可出示問題3進行過渡）

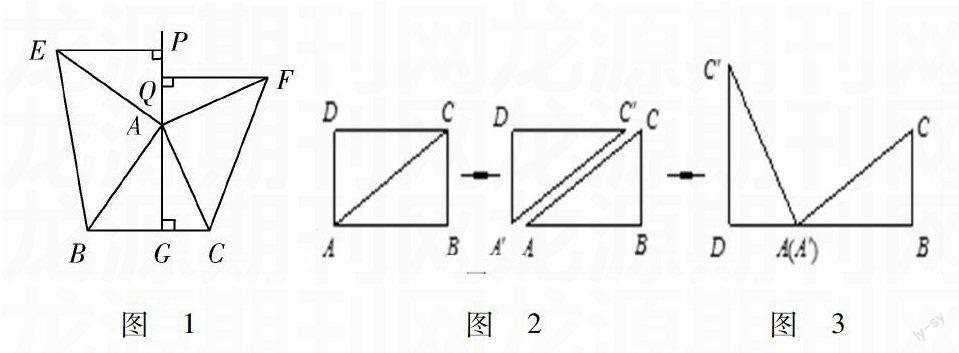
問題3：將矩形ABCD紙片沿對角線AC剪開，得到△ABC和△A′C′D，則△ABC和△A′C′D之間的關系式.如圖1所示.將△A′C′D的頂點A′與點A重合，并繞點A按逆時針方向旋轉，使點D、A（A′）、B在同一條直線上，如圖2所示.觀察圖2可知：與BC相等的線段是，∠CAC′=°.

圖 4分析 學生容易理解，容易解決，為后面的探究做好鋪墊，學生發現找一個與EP和FQ都相等的線段也就是劃歸為問題3中的基本圖形“蝴蝶型”全等.將圖4分解為兩個基本圖形，分別得Rt△ABG≌Rt△EAP，得出EP=AG.同樣Rt△ACG≌Rt△FAQ，得出FQ=AG.從而得證EP=FG.

五、激趣啟發

王梓坤院士曾指出：“數學教師的職責之一就在于培養學生對數學的興趣，這等于給了他們長久鉆研數學的動力，優秀的數學教師之所以在學生心中永志不忘，就是由于他點燃了學生心中熱愛數學的熊熊火焰”

興趣在教學中起著決定性的作用.教師設置的提問可以來源于生活，也可以來自數學本身或其他學科，要通過問題呈現刺激性的信息，激發學生的學習興趣，引發認知沖突，誘發質疑猜想，調動生學習的積極性、主動性.而在此過程中，教師只須因勢利導，巧妙點撥，可以很好地完成教學任務，而且會取得出人意料的教學效果.

在不等式教學中，我們常感到很抽象.例如：ab

六、開放創新

低效率的數學課堂上教師拋出的問題數量不少，但是其中封閉性問題占大部分，開放性問題較少.若能設置適當的開放性的問題，一方面可以滿足不同水平學生能力的差異，另一方面可以使學生對數學多方位、多角度去聯想、思考、探索，有利于拓展學生思維的深度和廣度，培養學生的創新能力.

如在學習平行四邊形的判定時，有這樣一道題目：在四邊形ABCD中，AD∥BC，對角線AC與BD相交于點O，請添加一個條件，使四邊形ABCD成為平行四邊形.這是一道開放題，放在平行四邊形的判定的復習課上，能較好地復習判定方法，但在平時新課教學中，難度會太大.因此，這需要老師改編題目，讓題目的難度適合學生，比如可以加上：（1）添加條件后，可用“兩組對邊分別平行的四邊形是平行四邊形”來判斷.（2）添加條件后，可用“一組對邊平行且相等的四邊形是平行四邊形”來判斷.根據學生的具體情況，也可以有其他的改編形式.

【參考文獻】

[1]王梓坤.讓你開竅的數學[M].鄭州：河南科學技術出版社.1997.2.第46頁.

[2]羅增儒.中學數學課例分析[M]. 西安：陜西師范大學出版社.2001.2.第205頁.