理性對待“數(shù)學規(guī)定”，打造智慧課堂

谷衛(wèi)章

[摘 要]《義務(wù)教育數(shù)學課程標準》（2011年版）指出：“要讓學生理解‘規(guī)定’的合理性，并在這個過程中學會數(shù)學思考，感悟理性精神。”因此，數(shù)學教師要理性對待“數(shù)學規(guī)定”，讓學生不僅了解數(shù)學規(guī)定的表面現(xiàn)象，而且受到數(shù)學規(guī)定中隱含的數(shù)學智慧的潛移默化的影響，從而打造出理性的、充滿智慧的數(shù)學課堂。

[關(guān)鍵詞]理性 數(shù)學規(guī)定 小學數(shù)學 智慧課堂

[中圖分類號] G623.5 [文獻標識碼] A [文章編號] 1007-9068（2015）35-057

小學數(shù)學中有一類客觀性較強的知識，是約定俗成的，通常被稱為“數(shù)學規(guī)定”，如數(shù)學命名、數(shù)學符號、書寫格式、數(shù)學法則等。一直以來，關(guān)于數(shù)學規(guī)定的爭議很多，有的教師認為數(shù)學規(guī)定不適合讓學生討論或深究，因為這是說不清楚的事;有的認為如果教師一味地告訴學生這是規(guī)定，從學生長遠發(fā)展的角度來看，這樣會使學生過分依賴書本、迷信權(quán)威，不利于學生創(chuàng)新意識的培養(yǎng)。我認為，教師要科學地對待“數(shù)學規(guī)定”，打造出充滿智慧的數(shù)學課堂。

一、形象訴說，體現(xiàn)數(shù)學的溫情之意

數(shù)學教材中有許多關(guān)于符號、算法、算理、概念公式的讀法或者寫法，它們一般都有具有數(shù)學語言特色。對于這些數(shù)學規(guī)定，教師可以采取化抽象為具體的方法，使學生認識到數(shù)學規(guī)定的趣味和含義。

比如“+”，我們約定俗成，稱之為“加號”，“×”稱為“乘號”， “<”則稱作“小于號”……諸如此類的符號，學生在剛開始接觸時定然會感到萬分好奇，產(chǎn)生為什么要這樣稱呼的想法。此時，教師應(yīng)順著學生的學習疑惑，運用形象化的語言描述來揭開這些數(shù)學符號的神秘面紗。例如對于“+”，教師可以用“一橫加上一豎，有著合并、增加或者添上的意思”這樣的形象語言去解釋;對于“×”，教師可以從比較加號與乘號的外形入手，引導(dǎo)學生發(fā)現(xiàn)加號與乘號外形上的相似之處，從而猜測它們之間可能存在的聯(lián)系。

這樣溫情而又形象的教學語言，能加深學生對數(shù)學規(guī)定的認識，促進學生的理解，使課堂充滿智慧。

二、適當剖析，展現(xiàn)規(guī)定的本質(zhì)特點

數(shù)學教學的目的是讓學生通過數(shù)學學習，形成一定的數(shù)學思想和數(shù)學意識。在這個學習過程中，數(shù)學規(guī)定起到了顯著的作用，這是因為這些規(guī)定背后往往隱藏著深刻的道理。所以教師適時要引導(dǎo)學生對這些數(shù)學規(guī)定進行認真剖析，使學生從中感受到數(shù)學規(guī)定的本質(zhì)特點，深化理解。

在關(guān)于數(shù)的運算的教學中，教師大都是按照運算法則的硬性規(guī)定進行教學，對于為什么這樣規(guī)定等運算原理卻不加解釋，讓學生深感困惑。其實多數(shù)情況下，數(shù)學規(guī)定都是為了優(yōu)化計算或便于解決問題而制定的。如有位教師為了讓學生理解數(shù)學規(guī)定中運算順序的求簡原則，曾經(jīng)做了這樣一個形象的比喻：“自行車、汽車、火車、飛機是可供選擇的交通工具，從北京到上海，你會選擇哪種？”同樣的，我們可以考慮，在數(shù)數(shù)、加減、乘除這些計算方法中，既然數(shù)數(shù)就可以解決問題，為什么還要用其他計算方法呢？以“1+5×3”為例，5×3可變?yōu)?+5+5，所以通過數(shù)一數(shù)或者加一加都可以得到結(jié)果，那么為什么還要用乘法呢？這是因為用乘法比較簡便、快捷，比起數(shù)數(shù)和加法更妙。

無論是數(shù)學符號還是數(shù)學運算、概念公式等數(shù)學規(guī)定，都是有其存在道理的。它們或是便于記憶，或是便于理解……只要教師引導(dǎo)學生進行適當剖析，就可以幫助學生深刻領(lǐng)會到數(shù)學規(guī)定的內(nèi)涵。

三、巧妙溝通，體現(xiàn)數(shù)學的整體聯(lián)系

對于數(shù)學規(guī)定，教師應(yīng)從數(shù)學知識產(chǎn)生和發(fā)展的角度來解讀，使學生親身經(jīng)歷數(shù)學規(guī)定的形成與發(fā)展過程，從而深刻理解數(shù)學規(guī)定的意圖和作用。

如教學“分米和毫米”時，由于學生已經(jīng)認識了米與厘米，明白了各單位之間的換算關(guān)系，為使學生對所學知識形成系統(tǒng)的認識，教師可以借助“階梯式”的圖形（如下圖）來幫助學生理解“十進制”這個數(shù)學規(guī)定。在這樣直觀、具體的示意圖的幫助下，學生不僅能復(fù)習已經(jīng)學過的計數(shù)單位，還能對長度單位的規(guī)定有一個系統(tǒng)的知識建構(gòu)，從而將知識融會貫通。

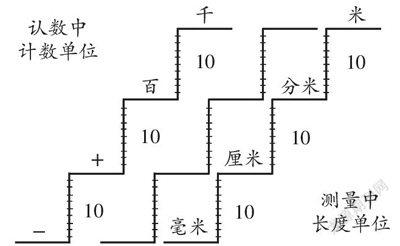
由此看來，在數(shù)學教學中，為深化學生對數(shù)學規(guī)定的認識，教師要及時引導(dǎo)學生深入了解相關(guān)的數(shù)學規(guī)定，將所學知識融會貫通。教師還可以借助形象生動的語言或者圖形，幫助學生理解和接受數(shù)學規(guī)定。

總之，數(shù)學本身是一門充滿理性精神的學科，教師不能只讓課堂教學僅僅停留在表面上，還要真正讓學生“知其然而且知其所以然”，使學生學會理性看待教材中的數(shù)學規(guī)定，辯證地看待數(shù)學規(guī)定的價值，從而讓數(shù)學規(guī)定的觀念根植于學生心中，促進數(shù)學學習。

（責編 吳美玲）