引導學生體驗生活培養數學應用能力

柯家文

摘要：數學教學不僅僅是知識的教學，更是一種過程教學、體驗教學。密切數學與生活之間的聯系，突破學科本位，體現教學生活化、活動化和情感化是數學新課程強調的重要教學目標。通過學生親自動手操作，經歷觀察、記錄、整理、分析、交流，加之于小組的密切合作，能夠更好地感受數學、體驗數學、應用數學。關鍵詞：數學體驗；探索；問題意識；生活情景；培養

愛因斯坦說過：“對一切來說，只有熱愛才是最好的老師。”在數學教學中，教師要努力挖掘數學與生活的聯系，將教學組織的深入淺出，生動有趣，讓學生感受到數學就在我們身邊，無處不在，無處不有。

一、觀察身邊事物，觸動生活積累，讓學生感受數學

課程內容的設計要力求從生活實際出發，從學生熟悉的感興趣的問題引入學習的主題，創設豐富的問題情境，用心營造一種學生能獨立思考。大膽質疑，積極主動參與的教學氛圍。實踐表明，學生有了強烈的問題意識，才會深入思考，才能創造性地提出問題和解決問題。

從學生身邊的數學問題引入，充分激發學生的思維，既要求學生從實踐中歸納結論，又要求學生把發現的結論用自己的文字語言或數學語言表達出來，盡可能讓抽象的數學概念在生活中找到原形。在教學中可充分運用網絡資源，選用富有生活情趣的動畫、圖景、貼近學生的生活的實例制作課件，溝通書本知識與現實生活的聯系，調動學生學習的積極性、主動性，點亮學生智慧的火光，使學生覺得學數學是有趣的、有用的，并熱愛數學。

案例1：《直線與圓的位置關系》的教學。上這節課的時候，以“同學們看過海上日出嗎?”引入新課，把同學們的思緒帶到廣闊的大海邊，在大腦的熒光屏上放映出太陽從海平面慢慢升起的畫面。然后引導學生按照以下三個步驟進行：

(1)勾勒生活形態：請同學們先在腦子里勾勒出太陽從海平面慢慢升起直至離開海平面的輪廓。

(2)抽象數學模型：學生說腦子里出現了藍色的平靜的海平面，紅色的朝陽。海平面的盡頭象是一條直線，紅色的太陽象是一個圓。

(3)總結認知規律：利用多媒體課件放映日出的全過程并把太陽抽象成一個圓，海平面抽象成一條直線，進而讓學生討論圓與直線有幾種位置關系?再用幾何畫版放映出圓與直線的位置關系的變化過程，最后歸納出圓與直線的相切、相交、相離的三種相對位置關系。該節課運用這種“生活化”的新課引入法取得了很好的效果。

教師所引入的生活畫面與形態越逼真，學生學習就越有興趣，理解得就越深刻，同時還培養了學生的想象力，激發了學生的學習主動性。

二、聯系日常生活，突出應用意識，讓學生體驗數學

探索是人類思維中最活躍、最生動、最富有魅力的活動。探索的結果往往導致問題的解決和新的發現。無論是布魯納主張的發現法，還是玻利亞倡導的數學啟發法，其精髓都是重在讓學生學會探索，學會發現。如布魯納所倡導的，不是把學習材料直接星現給學生，而是給出一些提示性的線索，通過問題啟發，做一做，想一想，試一試，議一議等方式，讓學生自己通過積極主動的探索活動來學習數學，提高學生的實踐探索能力。

現代心理學認為：教學時應設法為學生創設逼真的問題情境，喚起學生思考的欲望。荷蘭著名教育家弗霄登塔爾指出，要從學生的生活實際中發現和創造，即強調從學生熟悉的生活環境和生活經驗出發進行教學。讓學生置身于逼真的問題情境中，體驗數學學習與實際生活的聯系，品嘗到用所學知識解釋生活現象以及解決實際問題的樂趣，感受到借助數學的思想方法，解釋生活中常見的各種數學現象，如優惠措施、行程問題的最佳選擇、物品的分配等。《數學課程標準》指出，數學教學必須注意從學生的生活情境和感興趣的事物出發，為他們提供參與的機會，使他們體會到數學就在身邊，對數學產生親切感。

案例2：甲乙兩商店以同樣價格出售同樣的商品，并且各自推出不同的優惠方案：在甲店累計購買100元商品，再購買的商品按原價的90％收費；在乙店累計購買50元商品后，再購買的商品按原價的95％收費。

學生活動1——獨立思考以下幾個問題：

1、現有4個人，準備消費40元，80元，140元，160元，那么去哪家商店更合算，為什么?

2、甲商店購物款達多少元可以優惠?乙商店購物款達多少元可以優惠?

通過簡單數據的比較，學生猜想到：

①若劣汁購物不超過50元，則在兩家商場花費是一樣的。

②若累計購物超過50元，但不超過100元，則在乙商場購物花費小。

③若累計購物超過100元又可能存在有三種情況。

學生活動2——繼續分組討論結論③：(1)什么情況下，在甲商場購物花費小?(2)什么情況下，在乙商場購物花費小?(3)什么情況下，在兩家商場購物花費相同?若累計購物超過100元時，分別在什么情況下甲優惠、乙優惠、甲乙費用相等?

教師分析——設消費x元時(x>100)分別表示甲店、乙店的費用。根據哪個店優惠，即該店費用便小于另一個店的費用，于是建立不等關系。學生在教師啟發引導下得出結論③即累計購物超過100元而不到150元時，在乙商店購物省錢，累計購物恰好150元時，兩個商店購物花費一樣，累計購物超過150元時，在甲商店購物省錢。

學生獨立思考并歸納——根據甲、乙商店的銷售方案，顧客怎樣選擇商店購物能獲得更大優惠?你能為消費者設計一套方案嗎?

通過體驗如何選擇商場購物，感受實際生活中存在的不等關系，根據實際問題中的不等關系列出不等式，就把實際問題轉化為數學問題。這樣，學生就走出了從數學到數學的圈子，從生活中找數學，學生活中的數學，感受到數學是生活中處處存在的，學習數學是為了解決生活中的實際問題，使學生增強學習興趣，提高他們學習的積極性，調動學生學好數學的原動力。

三、注重動手實踐，解決生活問題，讓學生應用數學

一個人數學素質的優勢不在于其掌握數學知識的多少，也不在于其能解決多少數學難題，而在于他能不能應用數學知識去解決實際問題。構建學生數學應用的理念，是教學中必不可少的一個環節，在課堂教學中占有重要的地位。數學新課程體現了數學刻畫現實世界的過程和全貌，教師應在數學課程和教學中努力為學生提供生活背景和實踐機會。使學生逐步形成數學應用意識和應用能力。

案例3：為了讓學生能夠真正掌握“圓柱的側面展開圖”數學知識的應用，在教學中呈現“螞蟻怎么走最近?”這一鮮艷活潑的生活問題：

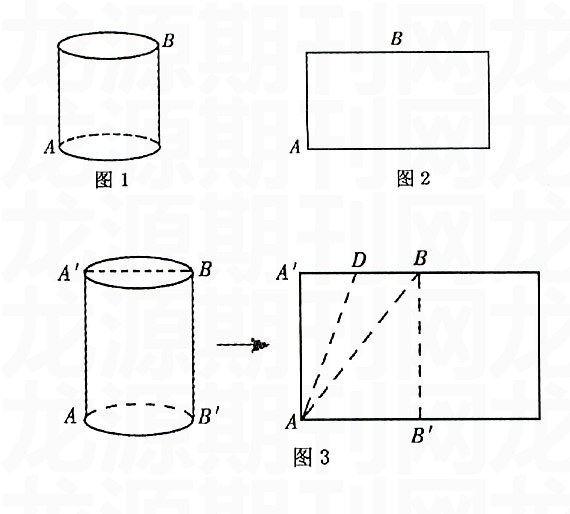
如圖1，有一個圓柱，它的高等于12厘米，底面半徑等于3厘米。在圓柱形的底面A點有一只螞蟻，它想吃到上底面上與A點相對的B點處的食物，需要爬行的最短路程是多少?(π的值取3)。

(1)同學們可自己做一個網柱，嘗試從A點到B點沿圓柱的側面畫出幾條路線，你覺得哪條路線最短呢?(小組討論)

(2)如圖2，將圓柱側面剪開展開成一個長方形，從A點到V點的最短路線是什么?你畫對了嗎?

(3)螞蟻從A點出發，想吃到B點上的食物，它沿圓柱側面爬行的最短路程是多少?(學生分組討論，教師公布結果并講解)

我們知道，圓柱的側面展開圖是一長方形。好了，現在咱們就用剪刀沿母線AA將圓柱的側面展開(如圖3)。

我們不難發現，剛才幾位同學的走法：(1)A→A′→B；(2)A→B′→B；(3)A→D→B；(4)M→B。

哪條路線是最短呢?你畫對了嗎?第(4)條路線最短。因為“兩點的所有連線中，線段最短”。

經過練習。學生發現這是一道與生活密切相關的問題。可見，學生經常接觸與生活聯系密切的數學問題，就會在現實生活中真正懂得如何應用數學。

當然，學生應用意識的提高還不能局限于某個知識點的應用上，由于學科活動本身具有的綜合性，所以只有通過設計與社會生活密切聯系的教學活動才能激發學生的學習興趣，增強應用的能力。例如，學習了解三角形后，讓學生測量學校旗桿的高度，測量山高；學習從部分看整體的教學中，可以組織學生到社會中調查某一種情況，引導學生收集數據，對數據進行整理、分析，得出結論；在制作剪紙和鑲邊的過程中，進一步理解軸對稱及其性質，體驗軸對稱在現實生活中的廣泛應用和豐富的文化價值等。這樣的實踐活動，更貼近學生生活。學生的應用能力得到了提高，思維得到了發展，數學整體素質也得到了提高。

綜上所述，只有在數學教學中強調從學生身邊的行為、自身的活動出發，激發學生對活動的參與熱情和學習興趣，才能體驗到生活中的數學，實現數學的應用價值，達到培養學生的主動性和創造性的目的。

參考文獻：

[1]黃新民_初中數學課堂創新教學理論與實踐[M]，杭州：浙江大學出版社，2004

[2]數學課程標準研制組編寫，數學新課程標準(實驗稿)解讀[M]，北京：北京師范大學出版社，2002

[3]課程教材研究所，中學數學課程教材研究開發中心，課程教學設計與案例[M]，北京：人民教育出版社，2004