體悟圖形運動，構建幾何模型，提升核心素養

張麗君

【摘要】幾何教學既是中考考查的重點，也是日常教學的難點，使用模型教學是幾何教學的重要手段.本文以“倍長中線”模型為例，通過創設問題情境，體悟圖形運動思想.借助典型例題，引導學生思考分析，構建8字型全等三角形模型.運用變式練習，進一步強化對模型的理解和應用，提高識圖技能，發展數學觀察能力，提升數學核心素養.

【關鍵詞】圖形運動；幾何模型；核心素養

2022年頒布的《義務教育數學課程標準》提出數學課程要培養學生的核心素養是“會用數學的眼光觀察現實世界，會用數學的思維思考現實世界，會用數學的語言表達現實世界”.初中數學內容分為五大板塊：數與數的運算、代數與方程、圖形與幾何、函數與分析、數據處理與概率統計.其中幾何教學既是中考考查的重點，也是日常教學的難點，使用模型教學是幾何教學的重要手段.

初中幾何模型是教師在長期的教學實踐中對具有一定相同特征的幾何圖形和問題的歸納，側重對某一解題方法、技巧的模仿和遷移運用.本文筆者以滬教版教材八年級上冊第十九章第2節“證明舉例”中的“倍長中線”教學設計為例，闡述如何在圖形運動思想指導下構建幾何模型，提升核心素養.

1 課前思考

1.1 教學目標

依據學生的認知規律和思維水平，本節課的教學目標設置如下：能夠識別模型，通過“倍長中線”構造8字型全等三角形模型，轉化已知條件進而解決問題.進一步獲得探究證明題思路的經歷，豐富演繹證明的經驗，體會在圖形運動思想的指導下添置輔助線和構造模型的方法，感受轉化思想.

1.2 教學重難點

學生在七年級已經學習過圖形的三種運動、全等和等腰三角形的相關知識，為本節課的研究奠定了基礎.本節課的教學重是點能夠識別模型，通過“倍長中線”構造8字型全等三角形模型，轉化已知條件進而解決問題；而如何利用“倍長中線”構造模型是本節課的難點.

2 課例設計

2.1 創設問題，引入模型

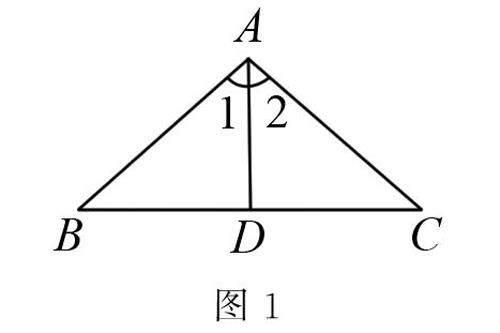
問題1 如圖1，D是BC上的一點，BD=CD，∠1=∠2.能否證明AB=AC呢？

解法1

證明：因為BD=CD，∠1=∠2

所以AB=AC（等腰三角形三線合一）

解法2

證明：在△ABD與△ACD中，

所以△ABD≌△ACD（SAS）

所以AB=AC（全等三角形的對應角相等）

問題2 解法一和解法二的方法正確嗎？錯誤在哪里？

問題3 在已有的圖形和條件無法解決問題的情況下，我們需要怎么辦？

問題4 如何添加輔助線？

設計意圖 通過創設問題，引導學生思考兩種證明思路存在的問題，復習回顧全等和等腰三角形的知識.學生分析發現無法在現有的圖形中解決問題，引導學生體悟圖形運動思想，利用將△ABD或△ACD旋轉構造“8字型全等三角形”模型，從而達到轉化邊和角的目的.

2.2 分析歸納，構建模型

問題1 什么是倍長中線？

問題2 遇到什么情況需要構建倍長中線模型？

問題3 如何構建倍長中線模型？

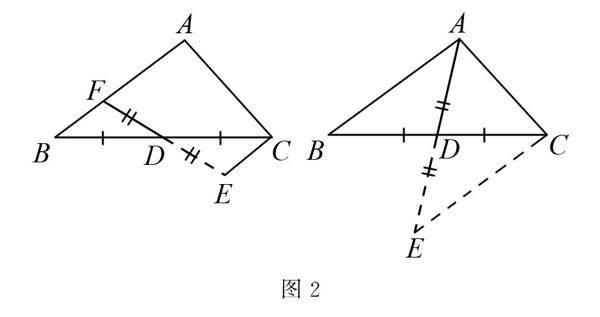
如圖2，當題目中出現中點時可以想到延長三角形的中線或過中點的線段（類中線），使得延長后的線段等于原來的兩倍，再聯結相應的端點構造8字型全等模型，從而達到轉化邊和角的目的.

設計意圖 引導學生歸納“倍長中線”的含義，提升數學語言表達能力.當已知條件中出現“中點”、“中線”時可以考慮倍長，構造8字型全等.通過分析歸納模型的特點，幫助學生在腦海中構建模型，加深對模型的理解，樹立模型意識，提升數學觀察能力.

2.3 典例精晰，運用模型

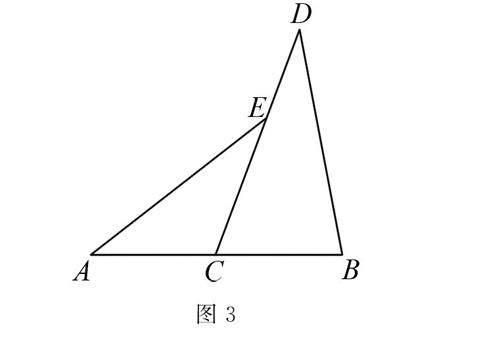
例題 已知，如圖3，C是AB的中點，點E在CD上，且∠AEC=∠D.

求證 AE=BD.

問題1 如何證明結論？全等三角形的性質可以嗎？等腰三角形的性質可以嗎？如何轉化條件？

問題2 如何添加輔助線？如圖4，延長DC至點F，使得DC=CF，聯結AF還是BF？還是都可以？

問題3 還可以添加別的輔助線嗎？如圖5，延長EC可以嗎？

設計意圖 通過典型例題的分析引導學生進一步體悟圖形運動思想，當題目中出現“中點”時可以聯想到需要“倍長中線”，建立8字型全等三角形模型.同時引導學生分析“延長DC至點F，使得DC=CF，聯結AF還是BF？”，當聯結BF時，無法構造8字型全等三角形，也無法轉移邊和角，從而是錯誤的輔助線.另外，引導學生一題多解，從不同的角度思考問題，如果輔助線是“延長EC至點F，使得EC = CF，則應該聯結BF”.

2.4 變式練習，鞏固模型

練習 已知，如圖6，C是AB的中點，點E在CD上，延長AE交BD于點G，聯結AD，且DG=EG.

求證 AE=BD.

問題1 如何添加輔助線？

問題2 延長DC至點F，使得DC=CF，聯結AF還是BF？還是都可以？

問題3 還可以添加別的輔助線嗎？延長EC可以嗎？

設計意圖 變式練習是在例題的基礎上改編而成，引導學生從復雜圖形中識別出基本模型.進一步鞏固通過“倍長中線”構建8字型全等模型，體會圖形的運動可以轉移邊和角.通過分析輔助線的聯結，培養學生數學思維，提升數學語言表達能力，培養學生核心素養.

2.5 暢談收獲，總結模型

請同學們談談自己的收獲，嘗試從“倍長中線”的概念、目的、模型、口訣、思想等方面進行總結.教師引導學生理解“倍：加倍—邊等；長：延長—對頂角；中線：邊等”，牢記“遇中線，想倍長；構全等，找關系”的口訣.

設計意圖 學生通過總結加深對“倍長中線”模型的理解，進一步體悟圖形的運動思想，培養學生的數學觀察能力、邏輯推理能力以及數學語言表達能力，提升數學核心素養.

2.6 分層作業，內化模型

基礎訓練 必做題

（1）已知，如圖7，在△ABC中，AB = 4，AC = 3，AD是BC的中線，則AD的取值范圍為.

能力提升 選做題

（2）已知，如圖8，CB、CD分別是鈍角△AEC和銳角△ABC的中線，且AC = AB.

求證：CE = 2CD.

拓展提高 選做題

（3）已知，如圖9，AD是△ABC的中線，點E、F分別在AB、AC上，且DE⊥DF，

求證：BE+CF＞EF.

設計意圖 分層作業主要是兼顧不同層次學生的實際需求，針對性地調控作業難度，促進每個孩子能在原有基礎上有所進步.

3 教學啟示

3.1 創設問題情境，體悟圖形運動

本節課是以滬教版八年級第一學期課本97頁第11題作為問題情境，首先分析在已有的圖形中能否借助已知條件解決問題.其次，進一步思考如何轉化條件從而解決問題.最后，教師引導學生借助圖形的運動改變圖形的位置，達到轉移邊和角的目的.在這個過程中，學生可以感悟到圖形的運動在幾何說理過程中的重要性.

3.2 學生自主思考，構建幾何模型

本節課通過典型例題的分析，找到題目中的題眼“中點”，由此聯想到“倍長中線”輔助線，構造8字型全等三角形.此題難點是倍長EC或DC之后是與A聯結還是與B聯結，學生自主思考分析，選擇聯結哪個點可以有效轉化條件，從而進行突破.在這個過程中，不僅培養學生的識圖能力，而且鍛煉學生的思維，提升模型意識和數學素養.

3.3注重變式練習，強化模型應用

變式訓練有助于學生更好地理解和掌握模型，培養學生在復雜圖形中抽象出數學模型的能力.本節課的變式練習是在典型例題的基礎上改編而成，聯結了AD，且延長AE交BD于點G.這道題目相比例題的圖形更加復雜，需要學生先識別出基礎模型，添加恰當的輔助線，在添加輔助線的時候同樣需要考慮聯結哪個端點可以有效轉化條件.通過這道變式訓練，不僅可以檢測本節課教學目標的達成程度，同時進一步加強學生對“倍長中線”模型的理解，再次體會圖形運動思想，強化模型應用能力.

3.4 發展識圖技能，提升核心素養

本節課問題引入、典例精晰、變式練習都緊扣主題，選取了具有代表性的題目.通過層層分析，引導學生歸納總結在何種情況下考慮“倍長中線”，“倍長中線”具體的方法以及“倍長中線”之后聯結哪個端點合適等.在這個過程中引導學生識圖、標圖，發展數學觀察能力，提升數學思維能力以及數學語言的表達能力.

參考文獻：

[1]吳剛平，安桂清，周文葉.新方案·新課標·新征程：《義務教育課程方案和課程標準（2022 年版）》 研讀[M].華東師范大學出版社，2022.

[2]鄭興民.初中數學幾何模型的教學誤區與解決路徑[J].福建教育學院學報，2022，23（09）：30-32.

[3]陳建.“雙減”下的初中數學建模思想訓練探究[J].福建教育學院學報，2022，23（06）：6-8.

[4]李洪明.如何有效開展初中數學幾何教學[J].科學大眾（科學教育），2019，（05）：14.